Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Nhiệt độ của miếng nhôm ngay khi có cân bằng nhiệt là 27oC.
b) Nhiệt lượng do quả cầu tỏa ra
Q1 = m1C1(t1 –t) = 0,2.880.(100 – 27) = 12848J
c) Nhiệt lượng do nước thu vào để tăng nhiệt độ đến 27oC
Q2 = m2C2(t-t2) = m2.4200.(27-20) = \(29400.m_2\)
Áp dụng phương trình cân bằng nhiệt, ta có:
Q1 = Q2 => 12848= \(29400.m_2\)
m2 =\(\frac{12848}{29400}=0,44kg\)
Vậy khối lượng của nước là 0,44kg.

Tóm tắt
\(m_1=0,2kg\)
\(t_1=100^0C\)
\(t_2=20^0C\)
\(t=27^0C\)
\(\Rightarrow\Delta t_1=t_1-t=100-27=73^0C\\ \Rightarrow\Delta t_2=t-t_2=27-20=7^0C\)
\(c_1=880J/kg.K\\ c_2=4200J/kg.K\)
_______________
\(m_2=?kg\)
Giải
Theo phương trình cân bằng nhiệt ta có:
\(Q_1=Q_2\\ \Leftrightarrow m_1.c_1.\Delta t_1=m_2.c_2.\Delta t_2\\ \Leftrightarrow0,2.880.73=m_2.4200.7\\ \Leftrightarrow m_2=0,44kg\)

Tham Khảo:
a) Nhiệt lượng do quả cầu tỏa ra là :
Qtỏa = m1.c1. (t°1 - t°3)
➩ Q tỏa = 0,2.880.(100-27)
➩ Q tỏa = 12848 J
b) Nhiệt lượng thu vào của nước là :
Qthu = m2.c2. (t°3 - t°2)
Vì Qthu = Q tỏa
➩ 12848 = m2. 4200.(27-20)
➪m2 = 12848/4200. (27-20)
➩m2 = 0,44kg

Nhiệt lượng quả cầu nhôm tỏa ra:
\(Q_{tỏa}=m_{Al}\cdot c_{Al}\cdot\left(t_1-t\right)\)
\(=0,15\cdot880\cdot\left(100-25\right)=9900J\)
Nhiệt lượng nước đã thu vào:
\(Q_{thu}=m_{nc}\cdot c_{nc}\cdot\left(t-t_2\right)\)
\(=m_{nc}\cdot4200\cdot\left(25-20\right)=21000m_{nc}\left(J\right)\)
Cân bằng nhiệt: \(Q_{thu}=Q_{tỏa}\)
\(\Rightarrow21000m_{nc}=9900\)
\(\Rightarrow m_{nc}=0,47kg\)
Không có đáp án

a.
Cân bằng nhiệt:
\(Q_{thu}=Q_{toa}=mc\left(t_1-t\right)=0,15\cdot880\cdot\left(100-25\right)=9900\left(J\right)\)
b.
Ta có: \(Q_{thu}=mc\left(t-t_1\right)\)
\(\Leftrightarrow9900=m\cdot4200\cdot\left(25-20\right)\)
\(\Leftrightarrow m\approx0,5\left(kg\right)\)
Ta có: \(m=DV\Rightarrow V=\dfrac{m}{D}=\dfrac{0,5}{1000}=5\cdot10^{-4}\left(m^3\right)\)

a.
Cân bằng nhiệt: \(Q_{thu}=Q_{toa}\)
\(\Leftrightarrow1\cdot4200\cdot\left(t-20\right)=0,5\cdot880\cdot\left(100-t\right)\)
\(\Leftrightarrow4200t-84000=44000-440t\)
\(\Leftrightarrow t\approx27,6^0C\)
Vậy sau 1 thời gian, nhiệt độ của quả cầu là 72,4 độ C và nước là 27,6 độ C
b.
Ta có: \(80\%Q_{toa}=Q_{thu}\)
\(\Leftrightarrow80\%\cdot0,5\cdot880\cdot\left(100-t\right)=1\cdot4200\cdot\left(t-20\right)\)
\(\Leftrightarrow35200-352t=4200t-84000\)
\(\Leftrightarrow t=26,2^0C\)
Nhiệt độ nước khi đó là 26,2 độ C
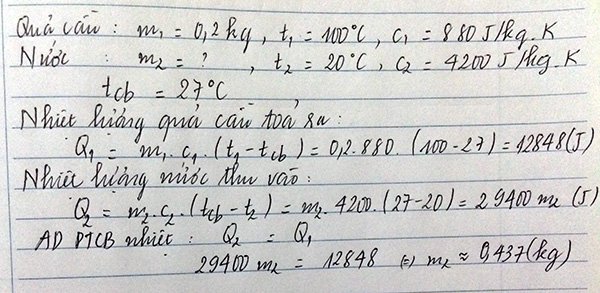

Tóm tắt:
\(m_1=0,2kg\)
\(t_1=100^oC\)
\(t_2=20^oC\)
\(t=27^oC\)
\(\Rightarrow\Delta t_1=t_1-t=100-27=73^oC\)
\(\Rightarrow\Delta t_2=t-t_2=27-20=7^oC\)
\(c_1=880J/kg.K\)
\(c_2=4200J/kg.K\)
==========
\(m_2=?kg\)
Do nhiệt lượng quả cầu tỏa ra bằng nhiệt lượng của nước thu vào nên ta có phương trình cân bằng nhiệt:
\(Q_1=Q_2\)
\(\Leftrightarrow m_1.c_1.\Delta t_1=m_2.c_2.\Delta t_2\)
\(\Leftrightarrow0,2.880.73=m_2.4200.7\)
\(\Leftrightarrow12848=29400m_2\)
\(\Leftrightarrow m_2=\dfrac{12848}{29400}\approx0,44\left(kg\right)\)
Tóm tắt
\(m_1=0,2kg\)
\(t_1=100^0C\)
\(t_2=20^0C\)
\(t=27^0C\)
\(c_1=880J/kg.K\)
\(c_2=4200J/kg.K\)
________________
\(m_2=?kg\)
Giải
Theo phương trình cân bằng nhiệt ta có
\(Q_1=Q_2\)
\(\Leftrightarrow m_1.c_1.\left(t_1-t\right)=m_2.c_2.\left(t-t_2\right)\)
\(\Leftrightarrow0,2.880.\left(100-27\right)=m_2.4200.\left(27-20\right)\)
\(\Leftrightarrow12848=29400m_2\)
\(\Leftrightarrow m_2=\dfrac{12848}{29400}\)
\(\Leftrightarrow m_2=0,44kg\)