
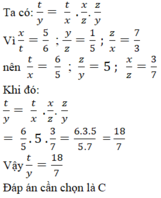
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

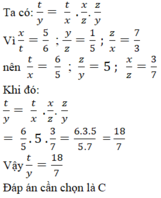

Bài 2:
Ta có: \(\dfrac{x-1}{65}+\dfrac{x-3}{63}=\dfrac{x-5}{61}+\dfrac{x-7}{59}\)
\(\Leftrightarrow\left(\dfrac{x-1}{65}-1\right)+\left(\dfrac{x-3}{63}-1\right)=\left(\dfrac{x-5}{61}-1\right)+\left(\dfrac{x-7}{59}-1\right)\)
\(\Leftrightarrow\left(x-66\right)\left(\dfrac{1}{65}+\dfrac{1}{63}-\dfrac{1}{61}-\dfrac{1}{59}\right)=0\)
=>x-66=0
hay x=66

1, ta co \(\frac{x}{5}=\frac{y}{6}=\frac{x}{20}=\frac{y}{24}\)
\(\frac{y}{8}=\frac{z}{7}=\frac{y}{24}=\frac{z}{21}\)
=>\(\frac{x}{20}=\frac{y}{24}=\frac{z}{21}=\frac{x+y-z}{20+24-21}=\frac{69}{23}=3\)
=>\(x=3\cdot20=60\)
\(y=3\cdot24=72\)
\(z=3\cdot21=63\)
3. ta co \(\frac{x}{15}=\frac{y}{7}=\frac{z}{3}=\frac{t}{1}=\frac{x+y-z+t}{15-7+3-1}=\frac{10}{10}=1\)
=> \(x=1\cdot15=15\)
\(y=1\cdot7=7\)
\(z=1\cdot3=3\)
\(t=1\cdot1=1\)

Đề dài quá nên mình làm từ từ.
a) Từ giả thiết ta có \(\frac{x}{15}=\frac{y}{7}=\frac{z}{3}=\frac{t}{1}\)
Áp dụng tính chất dãy tỉ số bằng nhau:
\(\frac{x}{15}=\frac{y}{7}=\frac{z}{3}=\frac{t}{1}=\frac{x-y+z-t}{15-7+3-1}=\frac{10}{10}=1\)
Từ đó suy ra x =15; y =7;z=3;t=1
Đúng ko ta:3
b) \(\left\{{}\begin{matrix}\frac{x}{5}=\frac{y}{6}\\\frac{y}{8}=\frac{z}{7}\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}\frac{x}{20}=\frac{y}{24}\\\frac{y}{24}=\frac{z}{21}\end{matrix}\right.\Rightarrow\frac{x}{20}=\frac{y}{24}=\frac{z}{21}\). Trở về dạng câu a:)
c)\(\left\{{}\begin{matrix}2x=3y\\5y=7z\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\frac{x}{3}=\frac{y}{2}\\\frac{y}{7}=\frac{z}{5}\end{matrix}\right.\). trở về dạng câu b:D

\(\hept{\begin{cases}\frac{x}{y}=\frac{2}{3}\\\frac{t}{y}=\frac{4}{9}\end{cases}}\Rightarrow\frac{x}{y}:\frac{t}{y}=\frac{2}{3}:\frac{4}{9}\Leftrightarrow\frac{x}{y}.\frac{y}{t}=\frac{2}{3}.\frac{9}{4}\Leftrightarrow\frac{x}{t}=\frac{3}{2}\)
\(\hept{\begin{cases}\frac{x}{t}=\frac{3}{2}\\\frac{z}{t}=\frac{5}{8}\end{cases}}\Rightarrow\frac{x}{t}:\frac{z}{t}=\frac{3}{2}:\frac{5}{8}\Leftrightarrow\frac{x}{t}.\frac{t}{z}=\frac{3}{2}.\frac{8}{5}\Leftrightarrow\frac{x}{z}=\frac{12}{5}\)

1) Tìm x, y, z biết:
\(\dfrac{x}{5}=\dfrac{y}{6}\Rightarrow\dfrac{x}{20}=\dfrac{y}{24}\) (1)
\(\dfrac{y}{8}=\dfrac{z}{7}\Rightarrow\dfrac{y}{24}=\dfrac{z}{21}\) (2)
Từ (1) và (2) suy ra:
\(\dfrac{x}{20}=\dfrac{y}{24}=\dfrac{z}{21}\) và x + y - z = 69
Áp dụng tính chất của dãy tỉ số bằng nhau:
\(\dfrac{x}{20}=\dfrac{y}{24}=\dfrac{z}{21}=\dfrac{x+y-z}{20+24-21}=\dfrac{69}{23}=3\)
\(\dfrac{x}{20}=3\Rightarrow\) x = 3 . 20 = 60
\(\dfrac{y}{24}=3\Rightarrow\) y = 3. 24 = 72
\(\dfrac{z}{21}=3\Rightarrow\) z = 3 . 21 = 63.

a)\(\left|2x-3y\right|+\left|2y-4z\right|=0\)
\(\left\{{}\begin{matrix}\left|2x-3y\right|\ge0\forall x;y\\\left|2y-4z\right|\ge0\forall y;z\end{matrix}\right.\) \(\Rightarrow\left|2x-3y\right|+\left|2y-4z\right|\ge0\)
Dấu "=" xảy ra khi:
\(\left\{{}\begin{matrix}\left|2x-3y\right|=0\\\left|2y-4z\right|=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}2x=3y\\2y=4z\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{x}{3}=\dfrac{y}{2}\\\dfrac{y}{4}=\dfrac{z}{2}\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{x}{6}=\dfrac{y}{4}\\\dfrac{y}{4}=\dfrac{z}{2}\end{matrix}\right.\)
\(\Rightarrow\dfrac{x}{6}=\dfrac{y}{4}=\dfrac{z}{2}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{6}=\dfrac{y}{4}=\dfrac{z}{2}=\dfrac{x+y+z}{6+4+2}=\dfrac{7}{12}\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{7}{12}.6=\dfrac{7}{2}\\y=\dfrac{7}{12}.4=\dfrac{7}{3}\\z=\dfrac{7}{12}.2=\dfrac{7}{6}\end{matrix}\right.\)
b)\(\left|x-2\right|+\left|x-3\right|+\left|x-4\right|=0\)
\(\left\{{}\begin{matrix}\left|x-2\right|\ge0\\\left|x-3\right|\ge0\\\left|x-4\right|\ge0\end{matrix}\right.\) \(\Leftrightarrow\left|x-2\right|+\left|x-3\right|+\left|x-4\right|\ge0\)
Dấu "=" xảy ra khi:
\(\left\{{}\begin{matrix}\left|x-2\right|=0\\\left|x-3\right|=0\\\left|x-4\right|=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=2\\x=3\\x=4\end{matrix}\right.\)
Vì \(2\ne3\ne4\) nên \(x\in\varnothing\)
c)
\(\left|x+1\right|+\left|x+2\right|+...+\left|x+8\right|+\left|x+9\right|\)
Với mọi \(x\ge0\) ta có:
\(\left\{{}\begin{matrix}\left|x+1\right|=x+1\\\left|x+2\right|=x+2\\\left|x+8\right|=x+8\\\left|x+9\right|=x+9\end{matrix}\right.\)\(\Leftrightarrow x+1+x+2+...+x+8+x+9=x-1\)
\(\Leftrightarrow9x+90=x-1\)
\(\Leftrightarrow9x=x-89\)
\(\Leftrightarrow-8x=89\)
\(\Leftrightarrow x=\dfrac{89}{-8}\left(KTM\right)\)
Với mọi \(x< 0\) ta có:
\(\left\{{}\begin{matrix}x+1=-x-1\\x+2=-x-2\\x+8=-x-8\\x+9=-x-9\end{matrix}\right.\) \(\Leftrightarrow\left(-x-1\right)+\left(-x-2\right)+...+\left(-x-8\right)+\left(-x-9\right)=x-1\)
\(\Leftrightarrow-9x-90=x-1\)
\(\Leftrightarrow-9x=x+89\)
\(\Leftrightarrow-10x=89\)
\(\Leftrightarrow x=\dfrac{89}{-10}\left(TM\right)\)
d)\(\left|2x-3y\right|+\left|5y-2z\right|+\left|2z-6\right|=0\)
\(\left\{{}\begin{matrix}\left|2x-3y\right|\ge0\\ \left|5y-2z\right|\ge0\\ \left|2z-6\right|\ge0\end{matrix}\right.\) \(\Leftrightarrow\left|2x-3y\right|+\left|5y-2z\right|+\left|2z-6\right|\ge0\)
Dấu "=" xảy ra khi:
\(\left\{{}\begin{matrix}\left|2x-3y\right|=0\\\left|5y-2z\right|=0\\\left|2z-6\right|=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}z=3\\y=\dfrac{6}{5}\\x=\dfrac{9}{5}\end{matrix}\right.\)

1,a/ Theo t,c dãy tỉ số bằng nhau ta có :
\(\dfrac{x}{2}=\dfrac{y}{5}=\dfrac{x+y}{2+5}=\dfrac{-14}{7}=2\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{x}{2}=-2\\\dfrac{y}{5}=-2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=-4\\y=-10\end{matrix}\right.\)
Vậy ...
b, Theo t,c dãy tỉ số bằng nhau ta có :
\(\dfrac{x}{7}=\dfrac{y}{5}=\dfrac{x-y}{7-5}=\dfrac{8}{2}=4\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{x}{7}=4\\\dfrac{y}{5}=4\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=28\\y=20\end{matrix}\right.\)
Vậy ...
2/a, Theo t,c dãy tỉ số bằng nhau ta có :
\(\dfrac{x}{2}=\dfrac{y}{5}=\dfrac{z}{7}=\dfrac{x+y+z}{2+5+7}=\dfrac{56}{14}=4\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{x}{2}=4\\\dfrac{y}{5}=4\\\dfrac{z}{7}=4\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=8\\y=10\\z=28\end{matrix}\right.\)
Vậy ...
b/ \(\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{z}{8}\)
\(\Leftrightarrow\dfrac{2x}{6}=\dfrac{y}{5}=\dfrac{z}{8}\)
Theo t,c dãy tỉ số bằng nhau ta có :
\(\dfrac{2x}{6}=\dfrac{y}{5}=\dfrac{z}{8}=\dfrac{2x+y-z}{6+5-8}=\dfrac{12}{3}=4\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2x}{6}=4\\\dfrac{y}{5}=4\\\dfrac{z}{8}=4\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=24\\y=20\\z=32\end{matrix}\right.\)
Vậy ..
Bài Giải:
Bài 1:
a) Theo đề bài, ta có:
\(\dfrac{x}{2}=\dfrac{y}{5}\)và x+y=-4
Áp dụng tính chất của dãy tỉ số bằng nhau
Ta có: \(\dfrac{x}{2}=\dfrac{y}{5}=\dfrac{x+y}{2+5}=\dfrac{-14}{7}=-2\)
Suy ra: x = 2 . (-2) =-4
y = 5 . (-2) =-10
Vậy: x = -4 và y = -10
Mấy câu sau cậu cứ dựa vào bài trên để giải nhé!
Tick cho Phong nhé:>
Yêu nhiều>3
#Phong_419

a) Có x, y, z tỉ lệ với 3, 5, 7 tức là \(\frac{x}{3}=\frac{y}{5}=\frac{z}{7}\)
x + y + z =210
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{x}{3}=\frac{y}{5}=\frac{z}{7}=\frac{x+y+z}{3+5+7}=\frac{210}{15}=14\)
\(\Rightarrow\left\{{}\begin{matrix}x=14.3=42\\y=14.5==70\\z=14.7=98\end{matrix}\right.\)
vậy...
b) Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{x}{5}=\frac{y}{6}=\frac{z}{7}=\frac{x-y+z}{5-6+7}=\frac{36}{6}=6\)
\(\Rightarrow\left\{{}\begin{matrix}x=6.5=30\\y=6.6=36\\z=6.7=42\end{matrix}\right.\)
vậy...
c)Vì BCNN (3; 4) = 12
\(\Rightarrow\frac{x}{2}=\frac{y}{3}\Leftrightarrow\frac{x}{2.4}=\frac{y}{3.4}=\frac{x}{8}=\frac{y}{12}\)
\(\Rightarrow\frac{y}{4}=\frac{z}{5}\Leftrightarrow\frac{y}{4.3}=\frac{z}{5.3}=\frac{y}{12}=\frac{z}{15}\)
\(\Rightarrow\frac{x}{8}=\frac{y}{12}=\frac{z}{15}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{x}{8}=\frac{y}{12}=\frac{z}{15}=\frac{2x+3y+5z}{16+36+75}=\frac{127}{127}=1\)
\(\Rightarrow\left\{{}\begin{matrix}x=1.8=8\\y=1.12=12\\z=1.15=15\end{matrix}\right.\)
Vậy...
a) Ta có:
x, y, z tỉ lệ với 3, 5, 7
⇒\(\frac{x}{3}=\frac{y}{5}=\frac{z}{7}=\frac{x+y+z}{3+5+7}=\frac{210}{15}=14\)
⇒\(\frac{x}{3}=\frac{y}{5}=\frac{z}{7}=14\Rightarrow\left\{{}\begin{matrix}x=42\\y=70\\z=98\end{matrix}\right.\)
b)\(\frac{x}{5}=\frac{y}{6}=\frac{z}{7}=\frac{x-y+z}{5-6+7}=\frac{36}{6}=6\)
⇒\(\frac{x}{5}=\frac{y}{6}=\frac{z}{7}=6\Rightarrow\left\{{}\begin{matrix}x=30\\y=36\\z=42\end{matrix}\right.\)
c)\(\frac{x}{2}=\frac{y}{3}\Rightarrow\frac{x}{2}.\frac{1}{4}=\frac{y}{3}.\frac{1}{4}\Rightarrow\frac{x}{8}=\frac{y}{12}\) (1)
\(\frac{z}{5}=\frac{y}{4}\Rightarrow\frac{z}{5}.\frac{1}{3}=\frac{y}{4}.\frac{1}{3}\Rightarrow\frac{z}{15}=\frac{y}{12}\) (2)
Từ (1) và (2) ⇒\(\frac{x}{8}=\frac{y}{12}=\frac{z}{15}=\frac{2x}{16}=\frac{3y}{36}=\frac{5z}{75}=\frac{2x+3y+5z}{16+36+75}=\frac{127}{127}=1\)
⇒\(\frac{x}{8}=\frac{y}{12}=\frac{z}{15}=1\Rightarrow\left\{{}\begin{matrix}x=8\\y=12\\z=15\end{matrix}\right.\)