Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

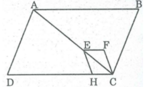
Ta có:
△ ABC = △ CDA (c.c.c) ⇒ S A B C = S C D A (1)
△ EFC = △ CHE (c.c.c) ⇒ S E F C = S C H E (2)
Từ (1) và (2) ⇒ S A B C - S E F C = S C D A - S C H E
Hay S A B C F E = S A E H D

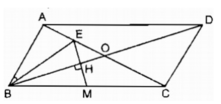
1) Vì ABCD là hình bình hành
=> OA=OC, OB=OD
Ta có: OM=OA/2
OP=OC/2
Mà OA=OC => OM=OP
Cm tương tự ta được OQ=ON
Tứ giác MNPQ có OM=OP. OQ=ON
=> MNPQ là hình bình hành
2) Tứ giác ANCQ có OA=OC (cmt), OQ=ON (cmt)
Suy ra tứ giác ANCQ là hình bình hành
Tứ giác BPDM có OB=OD (cmt), OM=OP (cmt)
Suy ra tứ giác BPDM là hình bình hành

Vì ABCD là hình bình hành và E là trung điểm của AO (vì BE là trung tuyến của tam giác ABO) nên ta có: AO = CO = 1/2 AC; AE = 1/2 AO.
Mặt khác, theo giả thiết AC = 2AB nên dễ thấy AB = AO và do đó AE = 1/2AB
Xét hai tam giác AEB và ABC, ta có:
Góc A chung
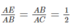
Vậy △ AEB đồng dạng △ ABC (c.g.c)
Suy ra: hai góc tương ứng bằng nhau ∠ ABE = ∠ ACB (đpcm)