Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1) ( 2m - 1 )x² - 2mx + 1 = 0
Ta có :
b² - 4ac
= (-2m)² - 4(2m - 1)
= 4m² - 8m + 4
= ( 2m - 2 )²
Như vậy : (2m - 2)² ≥ 0 , ∀m ∈ IR
Gọi x1 , x2 là 2 nghiệm của phương trình
Áp dụng hệ thức Vi-ét
{ x1 + x2 = 2m / (2m - 1)
{ x1x2 = 1 / (2m - 1)
Nếu nằm trong khoảng thì :
-1 < x1 < x2 < 0
Xét đoạn -1 < x1 < x2
<=> 0 < x1 + 1 < x2 + 1
Ta lập hệ pt sau
{ (x1 + 1 )(x2 + 1) > 0
{ x1 + 1 + x2 + 1 > 0
{ x1 + x1x2 + x2 + 1 > 0
{ x1 + x2 + 2 > 0
Sử dụng Vi-ét
=> 1/(2m - 1) + 2m/(2m - 1) + 1 > 0
=> 2m / (2m - 1) + 2 > 0
<=> ( 1 + 2m + 2m - 1 ) / (2m - 1) > 0
<=> [2m + 2(2m - 1)] / (2m - 1) > 0
<=> 4m / ( 2m - 1 ) > 0
<=> ( 2m + 4m - 2 ) / ( 2m - 1 ) > 0
<=> 4m / (2m - 1) > 0
<=> ( 6m - 2 ) / ( 2m - 1 ) > 0
Vẽ bảng xét dấu
<=> m < 0 V m > 1/2 (1)
<=> m < 1/2 V m > 3 (2)
Xét đoạn x1 < x2 < 0
{ x1 + x2 < 0
{ x1x2 > 0
{ 2m / (2m - 1) < 0
{ 1 / (2m - 1) > 0
Xét bảng xét dấu
<=> 0 < m < 1/2 (3)
<=> m > 1/2 (4)
=> m không thuộc khoảng nào cả
=> Vô nghiệm
2) x² + 2(m + 3)x + 4m + 12 = 0
Ta có
b² - 4ac
= [ 2(m + 3) ]² - 4(4m + 12)
= 4(m + 3)² - 16m - 48
= 4(m² + 6m + 9) - 16m - 48
= 4m² + 24m + 36 - 16m - 48
= 4m² + 8m - 12
Để pt có nghiệm m < -1 V m > 3
Gọi x1 , x2 là 2 nghiệm của pt
Áp dụng hệ thức Vi-ét
{ x1 + x2 = -2(m + 3)
{ x1x2 = 4m + 12
Ta đã có -1 < x1 < x2
<=> 0 < x1 + 1 < x2 + 1
Ta lập hệ bất pt sau :
{ ( x1 + 1 )(x2 + 1 ) > 0
{ x1 + 1 + x2 + 1 > 0
{ x1 + x1x2 + x2 + 1 > 0
{ x1 + x2 + 2 > 0
{ -2(m + 3) + 4m + 12 + 1 > 0
{ 4m + 12 + 2 > 0
{ -2m - 6 + 4m + 12 + 1 > 0
{ 4m + 14 > 0
{ 2m > -7
{ 4m > -14
{ m > -7/2
{ m > -7/2
Hợp nghiệm lại
m ∈ ( -7/2 ; -1 ) ∪ ( -3 ; +∞ )
3) 2x² + (2m - 1)x + m - 1 = 0
Ta có
b² - 4ac = (2m - 1)² - 4.2.(m - 1)
= 4m² - 4m + 1 - 8m + 8
= 4m² - 12m + 9
= ( 2m - 3 )²
Mà ( 2m - 3 )² ≥ 0 , ∀m ∈ IR
Gọi x1 và x2 là 2 nghiệm của pt
x1 = [-(2m - 1) - 2m +3 ]/ 2 = ( -4m + 2 ) /2 = -2m + 1
x2 = [-(2m - 1) +2m - 3 ]/ 2 = -2/2 = -1
Thế
3x1 - 4x2 = 11
3( -2m + 1 ) - 4.(-1) = 11
<=> -6m + 3 + 4 = 11
<=> -2m = 4
<=> m = -2
4) x² - 2(m - 3)x - 2(m - 1) = 0
Ta có
[ 2(m - 3)]² - 4.(-2)(m - 1)
= 4(m - 3)² + 8(m - 1)
= 4(m² - 6m + 9) + 8m - 8
= 4m² - 24m + 36 + 8m - 8
= 4m² - 16m + 28
Xét tiếp
(-16)² - 4.4.28 = -192 < 0 mà 4m² là số dương nên 4m² - 16m + 28 > 0 , ∀m ∈ IR
Áp dụng hệ thức Vi-ét
{ x1 + x2 = 2(m - 3)
{ x1x2 = -2(m - 1)
<=> ( x1 + x2 )² = 4(m - 3)²
<=> x1² + 2x1x2 + x2² = 4(m² - 6m + 9)
<=> x1² + x2² - (m - 1) = 4m² - 24m + 36
<=> x1² + x2² = 4m² - 24m + 36 + m - 1
<=> x1² + x2² = 4m² - 23m + 35
Để x1² + x2² Min thì 4m² - 23m + 35 phải Min
<=> 4m² - 23/4.2.2m + 529/16 + 31/16
<=> ( 2m - 23/4 )² + 31/16
Mà ( 2m - 23/4 )² ≥ 0 , ∀m ∈ IR
<=> ( 2m - 23/4 )² + 31/16 ≥ 31/16 > 0
Vậy đạt Min khi đó "=" xảy ra : 2m - 23/4 = 0
<=> m = 23/8
Vậy m = 23/8 thì x1² + x2² đạt Min
=> Amin = x1² + x2² = 4(23/8)² - 23(23/8) + 35 = 31/161) ( 2m - 1 )x² - 2mx + 1 = 0
Ta có :
b² - 4ac
= (-2m)² - 4(2m - 1)
= 4m² - 8m + 4
= ( 2m - 2 )²
Như vậy : (2m - 2)² ≥ 0 , ∀m ∈ IR
Gọi x1 , x2 là 2 nghiệm của phương trình
Áp dụng hệ thức Vi-ét
{ x1 + x2 = 2m / (2m - 1)
{ x1x2 = 1 / (2m - 1)
Nếu nằm trong khoảng thì :
-1 < x1 < x2 < 0
Xét đoạn -1 < x1 < x2
<=> 0 < x1 + 1 < x2 + 1
Ta lập hệ pt sau
{ (x1 + 1 )(x2 + 1) > 0
{ x1 + 1 + x2 + 1 > 0
{ x1 + x1x2 + x2 + 1 > 0
{ x1 + x2 + 2 > 0
Sử dụng Vi-ét
=> 1/(2m - 1) + 2m/(2m - 1) + 1 > 0
=> 2m / (2m - 1) + 2 > 0
<=> ( 1 + 2m + 2m - 1 ) / (2m - 1) > 0
<=> [2m + 2(2m - 1)] / (2m - 1) > 0
<=> 4m / ( 2m - 1 ) > 0
<=> ( 2m + 4m - 2 ) / ( 2m - 1 ) > 0
<=> 4m / (2m - 1) > 0
<=> ( 6m - 2 ) / ( 2m - 1 ) > 0
Vẽ bảng xét dấu
<=> m < 0 V m > 1/2 (1)
<=> m < 1/2 V m > 3 (2)
Xét đoạn x1 < x2 < 0
{ x1 + x2 < 0
{ x1x2 > 0
{ 2m / (2m - 1) < 0
{ 1 / (2m - 1) > 0
Xét bảng xét dấu
<=> 0 < m < 1/2 (3)
<=> m > 1/2 (4)
=> m không thuộc khoảng nào cả
=> Vô nghiệm
2) x² + 2(m + 3)x + 4m + 12 = 0
Ta có
b² - 4ac
= [ 2(m + 3) ]² - 4(4m + 12)
= 4(m + 3)² - 16m - 48
= 4(m² + 6m + 9) - 16m - 48
= 4m² + 24m + 36 - 16m - 48
= 4m² + 8m - 12
Để pt có nghiệm m < -1 V m > 3
Gọi x1 , x2 là 2 nghiệm của pt
Áp dụng hệ thức Vi-ét
{ x1 + x2 = -2(m + 3)
{ x1x2 = 4m + 12
Ta đã có -1 < x1 < x2
<=> 0 < x1 + 1 < x2 + 1
Ta lập hệ bất pt sau :
{ ( x1 + 1 )(x2 + 1 ) > 0
{ x1 + 1 + x2 + 1 > 0
{ x1 + x1x2 + x2 + 1 > 0
{ x1 + x2 + 2 > 0
{ -2(m + 3) + 4m + 12 + 1 > 0
{ 4m + 12 + 2 > 0
{ -2m - 6 + 4m + 12 + 1 > 0
{ 4m + 14 > 0
{ 2m > -7
{ 4m > -14
{ m > -7/2
{ m > -7/2
Hợp nghiệm lại
m ∈ ( -7/2 ; -1 ) ∪ ( -3 ; +∞ )
3) 2x² + (2m - 1)x + m - 1 = 0
Ta có
b² - 4ac = (2m - 1)² - 4.2.(m - 1)
= 4m² - 4m + 1 - 8m + 8
= 4m² - 12m + 9
= ( 2m - 3 )²
Mà ( 2m - 3 )² ≥ 0 , ∀m ∈ IR
Gọi x1 và x2 là 2 nghiệm của pt
x1 = [-(2m - 1) - 2m +3 ]/ 2 = ( -4m + 2 ) /2 = -2m + 1
x2 = [-(2m - 1) +2m - 3 ]/ 2 = -2/2 = -1
Thế
3x1 - 4x2 = 11
3( -2m + 1 ) - 4.(-1) = 11
<=> -6m + 3 + 4 = 11
<=> -2m = 4
<=> m = -2
4) x² - 2(m - 3)x - 2(m - 1) = 0
Ta có
[ 2(m - 3)]² - 4.(-2)(m - 1)
= 4(m - 3)² + 8(m - 1)
= 4(m² - 6m + 9) + 8m - 8
= 4m² - 24m + 36 + 8m - 8
= 4m² - 16m + 28
Xét tiếp
(-16)² - 4.4.28 = -192 < 0 mà 4m² là số dương nên 4m² - 16m + 28 > 0 , ∀m ∈ IR
Áp dụng hệ thức Vi-ét
{ x1 + x2 = 2(m - 3)
{ x1x2 = -2(m - 1)
<=> ( x1 + x2 )² = 4(m - 3)²
<=> x1² + 2x1x2 + x2² = 4(m² - 6m + 9)
<=> x1² + x2² - (m - 1) = 4m² - 24m + 36
<=> x1² + x2² = 4m² - 24m + 36 + m - 1
<=> x1² + x2² = 4m² - 23m + 35
Để x1² + x2² Min thì 4m² - 23m + 35 phải Min
<=> 4m² - 23/4.2.2m + 529/16 + 31/16
<=> ( 2m - 23/4 )² + 31/16
Mà ( 2m - 23/4 )² ≥ 0 , ∀m ∈ IR
<=> ( 2m - 23/4 )² + 31/16 ≥ 31/16 > 0
Vậy đạt Min khi đó "=" xảy ra : 2m - 23/4 = 0
<=> m = 23/8
Vậy m = 23/8 thì x1² + x2² đạt Min
=> Amin = x1² + x2² = 4(23/8)² - 23(23/8) + 35 = 31/161) ( 2m - 1 )x² - 2mx + 1 = 0
Ta có :
b² - 4ac
= (-2m)² - 4(2m - 1)
= 4m² - 8m + 4
= ( 2m - 2 )²
Như vậy : (2m - 2)² ≥ 0 , ∀m ∈ IR
Gọi x1 , x2 là 2 nghiệm của phương trình
Áp dụng hệ thức Vi-ét
{ x1 + x2 = 2m / (2m - 1)
{ x1x2 = 1 / (2m - 1)
Nếu nằm trong khoảng thì :
-1 < x1 < x2 < 0
Xét đoạn -1 < x1 < x2
<=> 0 < x1 + 1 < x2 + 1
Ta lập hệ pt sau
{ (x1 + 1 )(x2 + 1) > 0
{ x1 + 1 + x2 + 1 > 0
{ x1 + x1x2 + x2 + 1 > 0
{ x1 + x2 + 2 > 0
Sử dụng Vi-ét
=> 1/(2m - 1) + 2m/(2m - 1) + 1 > 0
=> 2m / (2m - 1) + 2 > 0
<=> ( 1 + 2m + 2m - 1 ) / (2m - 1) > 0
<=> [2m + 2(2m - 1)] / (2m - 1) > 0
<=> 4m / ( 2m - 1 ) > 0
<=> ( 2m + 4m - 2 ) / ( 2m - 1 ) > 0
<=> 4m / (2m - 1) > 0
<=> ( 6m - 2 ) / ( 2m - 1 ) > 0
Vẽ bảng xét dấu
<=> m < 0 V m > 1/2 (1)
<=> m < 1/2 V m > 3 (2)
Xét đoạn x1 < x2 < 0
{ x1 + x2 < 0
{ x1x2 > 0
{ 2m / (2m - 1) < 0
{ 1 / (2m - 1) > 0
Xét bảng xét dấu
<=> 0 < m < 1/2 (3)
<=> m > 1/2 (4)
=> m không thuộc khoảng nào cả
=> Vô nghiệm
2) x² + 2(m + 3)x + 4m + 12 = 0
Ta có
b² - 4ac
= [ 2(m + 3) ]² - 4(4m + 12)
= 4(m + 3)² - 16m - 48
= 4(m² + 6m + 9) - 16m - 48
= 4m² + 24m + 36 - 16m - 48
= 4m² + 8m - 12
Để pt có nghiệm m < -1 V m > 3
Gọi x1 , x2 là 2 nghiệm của pt
Áp dụng hệ thức Vi-ét
{ x1 + x2 = -2(m + 3)
{ x1x2 = 4m + 12
Ta đã có -1 < x1 < x2
<=> 0 < x1 + 1 < x2 + 1
Ta lập hệ bất pt sau :
{ ( x1 + 1 )(x2 + 1 ) > 0
{ x1 + 1 + x2 + 1 > 0
{ x1 + x1x2 + x2 + 1 > 0
{ x1 + x2 + 2 > 0
{ -2(m + 3) + 4m + 12 + 1 > 0
{ 4m + 12 + 2 > 0
{ -2m - 6 + 4m + 12 + 1 > 0
{ 4m + 14 > 0
{ 2m > -7
{ 4m > -14
{ m > -7/2
{ m > -7/2
Hợp nghiệm lại
m ∈ ( -7/2 ; -1 ) ∪ ( -3 ; +∞ )
3) 2x² + (2m - 1)x + m - 1 = 0
Ta có
b² - 4ac = (2m - 1)² - 4.2.(m - 1)
= 4m² - 4m + 1 - 8m + 8
= 4m² - 12m + 9
= ( 2m - 3 )²
Mà ( 2m - 3 )² ≥ 0 , ∀m ∈ IR
Gọi x1 và x2 là 2 nghiệm của pt
x1 = [-(2m - 1) - 2m +3 ]/ 2 = ( -4m + 2 ) /2 = -2m + 1
x2 = [-(2m - 1) +2m - 3 ]/ 2 = -2/2 = -1
Thế
3x1 - 4x2 = 11
3( -2m + 1 ) - 4.(-1) = 11
<=> -6m + 3 + 4 = 11
<=> -2m = 4
<=> m = -2
4) x² - 2(m - 3)x - 2(m - 1) = 0
Ta có
[ 2(m - 3)]² - 4.(-2)(m - 1)
= 4(m - 3)² + 8(m - 1)
= 4(m² - 6m + 9) + 8m - 8
= 4m² - 24m + 36 + 8m - 8
= 4m² - 16m + 28
Xét tiếp
(-16)² - 4.4.28 = -192 < 0 mà 4m² là số dương nên 4m² - 16m + 28 > 0 , ∀m ∈ IR
Áp dụng hệ thức Vi-ét
{ x1 + x2 = 2(m - 3)
{ x1x2 = -2(m - 1)
<=> ( x1 + x2 )² = 4(m - 3)²
<=> x1² + 2x1x2 + x2² = 4(m² - 6m + 9)
<=> x1² + x2² - (m - 1) = 4m² - 24m + 36
<=> x1² + x2² = 4m² - 24m + 36 + m - 1
<=> x1² + x2² = 4m² - 23m + 35
Để x1² + x2² Min thì 4m² - 23m + 35 phải Min
<=> 4m² - 23/4.2.2m + 529/16 + 31/16
<=> ( 2m - 23/4 )² + 31/16
Mà ( 2m - 23/4 )² ≥ 0 , ∀m ∈ IR
<=> ( 2m - 23/4 )² + 31/16 ≥ 31/16 > 0
Vậy đạt Min khi đó "=" xảy ra : 2m - 23/4 = 0
<=> m = 23/8
Vậy m = 23/8 thì x1² + x2² đạt Min
=> Amin = x1² + x2² = 4(23/8)² - 23(23/8) + 35 = 31/161) ( 2m - 1 )x² - 2mx + 1 = 0
Ta có :
b² - 4ac
= (-2m)² - 4(2m - 1)
= 4m² - 8m + 4
= ( 2m - 2 )²
Như vậy : (2m - 2)² ≥ 0 , ∀m ∈ IR
Gọi x1 , x2 là 2 nghiệm của phương trình
Áp dụng hệ thức Vi-ét
{ x1 + x2 = 2m / (2m - 1)
{ x1x2 = 1 / (2m - 1)
Nếu nằm trong khoảng thì :
-1 < x1 < x2 < 0
Xét đoạn -1 < x1 < x2
<=> 0 < x1 + 1 < x2 + 1
Ta lập hệ pt sau
{ (x1 + 1 )(x2 + 1) > 0
{ x1 + 1 + x2 + 1 > 0
{ x1 + x1x2 + x2 + 1 > 0
{ x1 + x2 + 2 > 0
Sử dụng Vi-ét
=> 1/(2m - 1) + 2m/(2m - 1) + 1 > 0
=> 2m / (2m - 1) + 2 > 0
<=> ( 1 + 2m + 2m - 1 ) / (2m - 1) > 0
<=> [2m + 2(2m - 1)] / (2m - 1) > 0
<=> 4m / ( 2m - 1 ) > 0
<=> ( 2m + 4m - 2 ) / ( 2m - 1 ) > 0
<=> 4m / (2m - 1) > 0
<=> ( 6m - 2 ) / ( 2m - 1 ) > 0
Vẽ bảng xét dấu
<=> m < 0 V m > 1/2 (1)
<=> m < 1/2 V m > 3 (2)
Xét đoạn x1 < x2 < 0
{ x1 + x2 < 0
{ x1x2 > 0
{ 2m / (2m - 1) < 0
{ 1 / (2m - 1) > 0
Xét bảng xét dấu
<=> 0 < m < 1/2 (3)
<=> m > 1/2 (4)
=> m không thuộc khoảng nào cả
=> Vô nghiệm
2) x² + 2(m + 3)x + 4m + 12 = 0
Ta có
b² - 4ac
= [ 2(m + 3) ]² - 4(4m + 12)
= 4(m + 3)² - 16m - 48
= 4(m² + 6m + 9) - 16m - 48
= 4m² + 24m + 36 - 16m - 48
= 4m² + 8m - 12
Để pt có nghiệm m < -1 V m > 3
Gọi x1 , x2 là 2 nghiệm của pt
Áp dụng hệ thức Vi-ét
{ x1 + x2 = -2(m + 3)
{ x1x2 = 4m + 12
Ta đã có -1 < x1 < x2
<=> 0 < x1 + 1 < x2 + 1
Ta lập hệ bất pt sau :
{ ( x1 + 1 )(x2 + 1 ) > 0
{ x1 + 1 + x2 + 1 > 0
{ x1 + x1x2 + x2 + 1 > 0
{ x1 + x2 + 2 > 0
{ -2(m + 3) + 4m + 12 + 1 > 0
{ 4m + 12 + 2 > 0
{ -2m - 6 + 4m + 12 + 1 > 0
{ 4m + 14 > 0
{ 2m > -7
{ 4m > -14
{ m > -7/2
{ m > -7/2
Hợp nghiệm lại
m ∈ ( -7/2 ; -1 ) ∪ ( -3 ; +∞ )
3) 2x² + (2m - 1)x + m - 1 = 0
Ta có
b² - 4ac = (2m - 1)² - 4.2.(m - 1)
= 4m² - 4m + 1 - 8m + 8
= 4m² - 12m + 9
= ( 2m - 3 )²
Mà ( 2m - 3 )² ≥ 0 , ∀m ∈ IR
Gọi x1 và x2 là 2 nghiệm của pt
x1 = [-(2m - 1) - 2m +3 ]/ 2 = ( -4m + 2 ) /2 = -2m + 1
x2 = [-(2m - 1) +2m - 3 ]/ 2 = -2/2 = -1
Thế
3x1 - 4x2 = 11
3( -2m + 1 ) - 4.(-1) = 11
<=> -6m + 3 + 4 = 11
<=> -2m = 4
<=> m = -2
4) x² - 2(m - 3)x - 2(m - 1) = 0
Ta có
[ 2(m - 3)]² - 4.(-2)(m - 1)
= 4(m - 3)² + 8(m - 1)
= 4(m² - 6m + 9) + 8m - 8
= 4m² - 24m + 36 + 8m - 8
= 4m² - 16m + 28
Xét tiếp
(-16)² - 4.4.28 = -192 < 0 mà 4m² là số dương nên 4m² - 16m + 28 > 0 , ∀m ∈ IR
Áp dụng hệ thức Vi-ét
{ x1 + x2 = 2(m - 3)
{ x1x2 = -2(m - 1)
<=> ( x1 + x2 )² = 4(m - 3)²
<=> x1² + 2x1x2 + x2² = 4(m² - 6m + 9)
<=> x1² + x2² - (m - 1) = 4m² - 24m + 36
<=> x1² + x2² = 4m² - 24m + 36 + m - 1
<=> x1² + x2² = 4m² - 23m + 35
Để x1² + x2² Min thì 4m² - 23m + 35 phải Min
<=> 4m² - 23/4.2.2m + 529/16 + 31/16
<=> ( 2m - 23/4 )² + 31/16
Mà ( 2m - 23/4 )² ≥ 0 , ∀m ∈ IR
<=> ( 2m - 23/4 )² + 31/16 ≥ 31/16 > 0
Vậy đạt Min khi đó "=" xảy ra : 2m - 23/4 = 0
<=> m = 23/8
Vậy m = 23/8 thì x1² + x2² đạt Min
=> Amin = x1² + x2² = 4(23/8)² - 23(23/8) + 35 = 31/161) ( 2m - 1 )x² - 2mx + 1 = 0
Ta có :
b² - 4ac
= (-2m)² - 4(2m - 1)
= 4m² - 8m + 4
= ( 2m - 2 )²
Như vậy : (2m - 2)² ≥ 0 , ∀m ∈ IR
Gọi x1 , x2 là 2 nghiệm của phương trình
Áp dụng hệ thức Vi-ét
{ x1 + x2 = 2m / (2m - 1)
{ x1x2 = 1 / (2m - 1)
Nếu nằm trong khoảng thì :
-1 < x1 < x2 < 0
Xét đoạn -1 < x1 < x2
<=> 0 < x1 + 1 < x2 + 1
Ta lập hệ pt sau
{ (x1 + 1 )(x2 + 1) > 0
{ x1 + 1 + x2 + 1 > 0
{ x1 + x1x2 + x2 + 1 > 0
{ x1 + x2 + 2 > 0
Sử dụng Vi-ét
=> 1/(2m - 1) + 2m/(2m - 1) + 1 > 0
=> 2m / (2m - 1) + 2 > 0
<=> ( 1 + 2m + 2m - 1 ) / (2m - 1) > 0
<=> [2m + 2(2m - 1)] / (2m - 1) > 0
<=> 4m / ( 2m - 1 ) > 0
<=> ( 2m + 4m - 2 ) / ( 2m - 1 ) > 0
<=> 4m / (2m - 1) > 0
<=> ( 6m - 2 ) / ( 2m - 1 ) > 0
Vẽ bảng xét dấu
<=> m < 0 V m > 1/2 (1)
<=> m < 1/2 V m > 3 (2)
Xét đoạn x1 < x2 < 0
{ x1 + x2 < 0
{ x1x2 > 0
{ 2m / (2m - 1) < 0
{ 1 / (2m - 1) > 0
Xét bảng xét dấu
<=> 0 < m < 1/2 (3)
<=> m > 1/2 (4)
=> m không thuộc khoảng nào cả
=> Vô nghiệm
2) x² + 2(m + 3)x + 4m + 12 = 0
Ta có
b² - 4ac
= [ 2(m + 3) ]² - 4(4m + 12)
= 4(m + 3)² - 16m - 48
= 4(m² + 6m + 9) - 16m - 48
= 4m² + 24m + 36 - 16m - 48
= 4m² + 8m - 12
Để pt có nghiệm m < -1 V m > 3
Gọi x1 , x2 là 2 nghiệm của pt
Áp dụng hệ thức Vi-ét
{ x1 + x2 = -2(m + 3)
{ x1x2 = 4m + 12
Ta đã có -1 < x1 < x2
<=> 0 < x1 + 1 < x2 + 1
Ta lập hệ bất pt sau :
{ ( x1 + 1 )(x2 + 1 ) > 0
{ x1 + 1 + x2 + 1 > 0
{ x1 + x1x2 + x2 + 1 > 0
{ x1 + x2 + 2 > 0
{ -2(m + 3) + 4m + 12 + 1 > 0
{ 4m + 12 + 2 > 0
{ -2m - 6 + 4m + 12 + 1 > 0
{ 4m + 14 > 0
{ 2m > -7
{ 4m > -14
{ m > -7/2
{ m > -7/2
Hợp nghiệm lại
m ∈ ( -7/2 ; -1 ) ∪ ( -3 ; +∞ )
3) 2x² + (2m - 1)x + m - 1 = 0
Ta có
b² - 4ac = (2m - 1)² - 4.2.(m - 1)
= 4m² - 4m + 1 - 8m + 8
= 4m² - 12m + 9
= ( 2m - 3 )²
Mà ( 2m - 3 )² ≥ 0 , ∀m ∈ IR
Gọi x1 và x2 là 2 nghiệm của pt
x1 = [-(2m - 1) - 2m +3 ]/ 2 = ( -4m + 2 ) /2 = -2m + 1
x2 = [-(2m - 1) +2m - 3 ]/ 2 = -2/2 = -1
Thế
3x1 - 4x2 = 11
3( -2m + 1 ) - 4.(-1) = 11
<=> -6m + 3 + 4 = 11
<=> -2m = 4
<=> m = -2
4) x² - 2(m - 3)x - 2(m - 1) = 0
Ta có
[ 2(m - 3)]² - 4.(-2)(m - 1)
= 4(m - 3)² + 8(m - 1)
= 4(m² - 6m + 9) + 8m - 8
= 4m² - 24m + 36 + 8m - 8
= 4m² - 16m + 28
Xét tiếp
(-16)² - 4.4.28 = -192 < 0 mà 4m² là số dương nên 4m² - 16m + 28 > 0 , ∀m ∈ IR
Áp dụng hệ thức Vi-ét
{ x1 + x2 = 2(m - 3)
{ x1x2 = -2(m - 1)
<=> ( x1 + x2 )² = 4(m - 3)²
<=> x1² + 2x1x2 + x2² = 4(m² - 6m + 9)
<=> x1² + x2² - (m - 1) = 4m² - 24m + 36
<=> x1² + x2² = 4m² - 24m + 36 + m - 1
<=> x1² + x2² = 4m² - 23m + 35
Để x1² + x2² Min thì 4m² - 23m + 35 phải Min
<=> 4m² - 23/4.2.2m + 529/16 + 31/16
<=> ( 2m - 23/4 )² + 31/16
Mà ( 2m - 23/4 )² ≥ 0 , ∀m ∈ IR
<=> ( 2m - 23/4 )² + 31/16 ≥ 31/16 > 0
Vậy đạt Min khi đó "=" xảy ra : 2m - 23/4 = 0
<=> m = 23/8
Vậy m = 23/8 thì x1² + x2² đạt Min
=> Amin = x1² + x2² = 4(23/8)² - 23(23/8) + 35 = 31/16

a: \(f\left(-2\right)=2\cdot\left(-2\right)^3+\left(-2\right)^2-4\cdot\left(-2\right)-2=-6\)
\(f\left(-1\right)=2\cdot\left(-1\right)^3+\left(-1\right)^2-4\cdot\left(-1\right)-2=-2+1+4-2=1\)
\(f\left(-\dfrac{1}{2}\right)=2\cdot\dfrac{-1}{8}+\dfrac{1}{4}-4\cdot\dfrac{-1}{2}-2=\dfrac{-1}{4}+\dfrac{1}{4}+2-2=0\)
\(f\left(1\right)=2+1-4-2=-3\)
\(f\left(2\right)=2\cdot2^3+2^2-4\cdot2-2=16+4-8-2=10\)
b: Vì f(-1/2)=0 nên -1/2 là một nghiệm của đa thức f(x)

cho 2014=2013+1 thay vào ta có:\(B=x^{2013}-\left(2013+1\right)x^{2012}+\left(2013+1\right)x^{2011}-...-\left(2013+1\right)x^2+\left(2013+1\right)x-1\)
\(=x^{2013}-\left(x+1\right)x^{2012}+\left(x+1\right)x^{2011}-...-\left(x+1\right)x^2+\left(x+1\right)x-1\)
\(=x^{2013}-x^{2013}-x^{2012}+x^{2012}+x^{2011}-...-x^3-x^2+x^2+x-1\)
\(=x-1=2013-1=2012\)

a: =>x+3>0
hay x>-3
b: \(\Leftrightarrow-\left(x-2\right)^2\left(x+2\right)>0\)
=>x+2<0
hay x<-2
c: =>x+4>0
hay x>-4
d: =>-3<x<4

Câu 1.
A = {15;16;17;18;19} (0,25đ)
Câu 2.
a. 2.(72 – 2.32) – 60
= 2.(49 – 2.9) – 60 (0,25đ)
= 2.31 – 60 (0,25đ)
= 62 – 60 = 2 (0,25đ)
b. 27.63 + 27.37
= 27.(63 + 37) (0,25đ)
= 27.100 (0,25đ)
= 2700 (0,25đ)
c. l-7l + (-8) + l-11l + 2
= 7 + (-8) + 11 + 2 (0,5 đ)
= 12 (0,25đ)
d. 568 – 34 {5.l9 – ( 4-1)2l + 10}
= 568 – 34 {5.[9-9] + 10} (0,25đ)
= 568 – 34.10
= 568 – 340 (0,25đ)
= 228 (0,25đ)
Câu 3.
a)2x + 3 = 52 : 5
2x + 3 =5 (0,25đ)
2x = 5-3 (0,25đ)
2x =2 (0,25đ)
x=1 (0,25đ)
b)
105 – ( x + 7) = 27 : 25
105 – ( x + 7) = 22 (0,25đ)
105 – ( x + 7) = 4 (0,25đ)
x + 7 = 105 – 4 (0,25đ)
x + 7 = 101 (0,25đ)
x = 101 – 7 (0,25đ)
x = 94 (0,25đ)
Câu 4.
Gọi x (hs) là số học sinh lớp 6B phải tìm (30<x< 38, x)
Vì hs lớp 6B xếp 2, hàng, 4 hàng, 8 hàng đều vừa đủ nên x⋮2; x⋮4; x⋮8 hay x ∈ BC{2;4;8} (0,25đ)
Ta có: BCNN(2,4,8) = 8 (0,25đ)
⇒ BC(2,4,8) = B(8) ={0; 8; 16;24; 32; 40; …}
Mặt khác: 30<x< 38 (0,25đ)
Nên x = 32
Vậy số học sinh lớp 6B là 32 học sinh (0,25đ)
Câu 5.
Khi M nằm giữa và cách đều hai điểm A và B (0,5đ)
Vẽ được hình có điểm M là trung điểm của AB (0,5đ)
Câu 6.a)

0,25đ
Điểm A nằm giữa O và B (0,25đ)
Vì OA < OB ( 4 < 8 ) (0,25đ)
Ta có: AO + AB = OB
3 + AB = 6 (0,25đ)
AB = 6 -3 = 3 cm (0,25đ)
Vậy OA = AB = 3 cm (0,25đ)
b)
Vì A nằm giữa O, B và cách đều O và B ( OA = AB ) (0,25đ)
Nên A là trung điểm OB (0,25đ)

Cho tam giác ABC đều
D thuộc AB , E thuộc AC sao cho BD = AE
CM : Khi D,E thay đổi ( di chuyển ) trên AB,AC thì đường trung tuyến DE luôn đi qua điểm cố định
Help me !!!

a)A=x+3/x-2
A=x-2+5/x-2
A=1+5/x-2
vì 1 thuộc Z nên để A thuộc Z thì 5 phải chia hết cho x-2
x-2 thuộc ước của 5
x-2 thuộc -5;-1;1;5
x = -3;1;3 hoặc 7
giá trị các biểu thức theo giá trị của x như trên và lần lượt là 0;-4;6;2
b)để B= 1-2x/2+x thuộc Z thì
1-2x phải chia hết cho 2+x
nên 1-2x-4+4 phải chia hết cho x+2
1-(2x+4)+4 phải chia hết cho x+2
1+4-[2(x+2] phải chia hết cho x+2
5 -[2(x+2] phải chia hết cho x+2
vì [2(x+2] chia hết cho x+2 nên 5 phải chia hết cho x+2
suy ra x+2 thuộc ước của 5
x+2 thuộc -5;-1;1;5
x=-7;-3;-1;3
giá trị các biểu thức theo giá trị của x như trên và lần lượt là -3;-7;3;-1

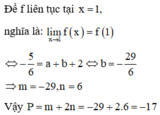


Đáp án B