K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
27 tháng 4 2016
TA CÓ: 
= 1+\(\frac{1}{2^2}\)+\(\frac{1}{3^2}\)+.....+\(\frac{1}{49^2}\)+\(\frac{1}{50^2}\)<1+ \(\frac{1}{1\times2}\)+\(\frac{1}{2\times3}\)+....+\(\frac{1}{49\times50}\)
= 1+ 1- \(\frac{1}{2}\) + \(\frac{1}{2}\) - \(\frac{1}{3}\) + ..... + \(\frac{1}{49}\) - \(\frac{1}{50}\)
= 1+ 1 - \(\frac{1}{50}\)
= 1+ \(\frac{49}{50}\) < 2
Chứng tỏ A < 2
22 tháng 4 2016
A=1+1/2^2+1/3^2+...+1/50^2
A<1+1/1*2+1/2*3+...+1/49*50
A<1+1/1-1/2+1/2-1/3+...+1/49-1/50
A<1+1-1/50
A<2-1/50<2
KL: vậy A<2
24 tháng 4 2016
\(S=3+\frac{3}{2}+\frac{3}{2^2}+...+\frac{3}{2^9}\)
\(\Leftrightarrow2S=9+3+\frac{3}{2}+...+\frac{3}{2^8}\)
\(\Leftrightarrow2S-S=9-\frac{3}{2^9}\)
\(\Leftrightarrow S=9-\frac{3}{2^9}=\frac{4605}{512}\)
Vậy S = \(\frac{4605}{512}\)
HP
24 tháng 4 2016
S=3+3/2+3/22+.....+3/29
S=3.(1+1/2+1/22+....+1/29)
Đặt A=1+1/2+1/22+......+1/29)
Ta có:2A=2+1+1/2+....+1/28
=>2A-A=(2+1+1/2+....+1/28)-(1+1/2+1/22+....+1/29)
=>A=2-1/29
Khi đó S=3.(2-1/29)=6-3/29=3069/512
28 tháng 1 2022
\(\dfrac{1}{2}S=\dfrac{3}{2}+\dfrac{3}{2^2}+...+\dfrac{3}{2^{10}}\)
\(\Leftrightarrow S\cdot\dfrac{1}{2}=\dfrac{3\cdot2^{10}-3}{2^{10}}\)
hay \(S=\dfrac{3\cdot2^{10}-3}{2^9}\)
27 tháng 4 2016
Chào bạn, bạn hãy theo dõi câu trả lời của mình nhé!
Ta có :
\(S=3+\frac{3}{2}+\frac{3}{2^2}+...+\frac{3}{2^9}\)
\(=>2S=6+3+\frac{3}{2}+...+\frac{3}{2^8}\)
\(2S-S=\left(6+3+\frac{3}{2}+...+\frac{3}{2^8}\right)-\left(3+\frac{3}{2}+\frac{3}{2^2}+...+\frac{3}{2^9}\right)\)
\(S=6-\frac{3}{2^9}=6-\frac{3}{512}=\frac{3072}{512}-\frac{3}{512}=\frac{3069}{512}\)
HP
27 tháng 4 2016
\(S=3+\frac{3}{2}+\frac{3}{2^2}+....+\frac{3}{2^9}\)
\(S=3.\left(1+\frac{1}{2}+\frac{1}{2^2}+....+\frac{1}{2^9}\right)\)
Đặt \(P=1+\frac{1}{2}+\frac{1}{2^2}+...+\frac{1}{2^9}\)
\(=>2P-P=\left(2+1+\frac{1}{2}+...+\frac{1}{2^8}\right)-\left(1+\frac{1}{2}+\frac{1}{2^2}+...+\frac{1}{2^9}\right)\)
\(=>P=2-\frac{1}{2^9}=\frac{1023}{512}\)
\(=>S=3.P=3.\frac{1023}{512}=\frac{3069}{512}\)
29 tháng 4 2016
Câu 1.
Muốn nhân hai phân số, ta nhân các tử với nhau và nhân các mẫu với nhau. (1 điểm)
Ví dụ:
0,5 điểm
b) Muốn chia một phân số hay một số nguyên cho một phân số, ta nhân số bị chia với số nghịch đảo của số chia (1 điểm)
Ví dụ:
0,5 điểm
Câu 2. ( 2 điểm)
Tia phân giác của một góc là tia nằm giữa hai cạnh của góc và tạo với hai cạnh ấy hai góc bằng nhau (1 điểm)
Câu 3. ( 2 điểm) mỗi ý đúng 0,5 điểm
Câu 4.
0,5 điểm
Câu 5. ( 1 điểm)
Số học sinh nữ lớp 6A là: 20 . 3/10 = 6 (HS) (0,5 điểm)
Số học sinh nam lớp 6A là: 20 – 6 = 14 (HS) (0,5 điểm)
Câu 6. ( 1,5 điểm)
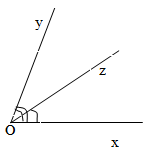
a) Vì ∠ xOz < ∠ xOy ( 350 <700) nên
tia Oz nằm giữa 2 tia Ox và Oy.
b) Vì tia Oz nằm giữa hai tia Ox và Oy nên
∠xOz + ∠zOy= ∠xOy hay 350 + ∠zOy = 700
=> ∠yOz = 350
c) Vì tia Oz nằm giữa hai tia Ox và Oy
và ∠xOz = ∠yOz = 350
nên Oz là tia phân giác của góc xOy
Q
14 tháng 3 2016
Câu hỏi của Sáng Đường - Chuyên mục hỏi đáp - Giúp tôi giải toán. - Học toán với OnlineMath
13 tháng 4 2016
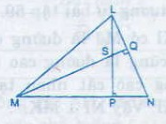
a) Chứng minh NS ⊥ LM
b) Khi =500, hãy tính góc MSP và góc PSQ
Hướng dẫn:
a) Trong ∆NML có :
LP ⊥ MN nên LP là đường cao
MQ ⊥ NL nên MQ là đường cao
mà PL ∩ MQ = {S}
suy ra S là trực tâm của tam giác nên đường thằng SN chứa đường cao từ N hay
SN ⊥ ML
b) ∆NMQ vuông tại Q có =500 nên
=400
∆MPS vuông tại Q có =400 nên
=500
Suy ra =1300(kề bù)
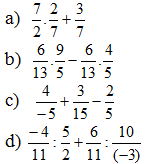
Ta có :
\(\frac{1}{1^2}< \frac{1}{1.2};\frac{1}{2^2}< \frac{1}{2.3};...;\frac{1}{50^2}< \frac{1}{49.50}\)
\(\Leftrightarrow\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+...+\frac{1}{50^2}< \frac{1}{1.2}+\frac{1}{2.3}+...+\frac{1}{49.50}=1-\frac{1}{50}< 1< 2\)
Vậy A < 2
\(\frac{1}{1^2}=1\)
\(\frac{1}{2^2}< \frac{1}{1.2}\)
\(\frac{1}{3^2}< \frac{1}{2.3}\)
\(...\)
\(\frac{1}{50^2}< \frac{1}{49.50}\)
\(\Rightarrow\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+...+\frac{1}{50^2}< 1+\frac{1}{1.2}+\frac{1}{2.3}+...+\frac{1}{49.50}\)
\(\Rightarrow A< 1+1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+...+\frac{1}{49}-\frac{1}{50}\)
\(\Rightarrow A< 1+1-\frac{1}{50}\)
\(\Rightarrow A< 2-\frac{1}{50}< 2\)
Vậy \(A< 2\)