Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

bài 1 : AH = \(\sqrt{119}\)cm
bài 2 : BN = \(\sqrt{49.54}\)cm
* hình tự vẽ
1/
Xét tam giác ABC: tam giác ABC là tam giác cân(gt) mà AH là đường cao(vì AH\(\perp\)BC)=> AH cũng là đường trung tuyến=> BH=HC
Ta có: BC=HB+HC, mà HB=HC(cmt)=> HB=HC=\(\frac{BC}{2}\)=> HB=HC= 5cm
Xét tam giác ACH, theo định lý Py ta go, có:
AH^2+ HC^2=AC^2
=> AH^2+ 5^2= 12^2
=> AH^2= 144-25
=> AH^2= 119=> AH= căn 119cm
2/ Xét tam giác BCA, theo định lý Py ta go, có:
BA^2+ AC^2= BC^2=> 12^2+5^2=BC^2
=> 144+25= BC^2=> BC^2= 169=>BC=13cm
Mà M là trung điểm BC(gt)=> MB=MC nên ta có BC=MB+MC=> MB=MC=\(\frac{BC}{2}\)=> MB=MC=6,5
Xét tam giác BMN, theo định lý Py ta go, có:
BN^2+NM^2= BM^2
=> BN^2+2,7^2=6,5^2=> BN^2 = 42,25-7,29=> BM^2= 34,96=> BM= căn 34,96cm

Xét tam giác BAH
Có B+BAH=900(vì tam giác BAH vuông tại H)
500+BAH=900
=>BAH=900-500
=>BAH=400
Xét tam giác HAC
Có C+HAC=900(Tam giác HAC vuông tại H)
400+HAC= 900
HAC=900-400
HAC=500
B)Xét tam giác ABH
Có AB2 = HB2+AH2(Theo định lý Pi-ta-go)
AB2=32+42
AB2=25=52
AB=5
Xét tam giác CAH
Có AC2=AH2+HC2 (Theo định lý Pi-ta-go)
AC2=42+42=32=

Áp dụng định lí Pytago vào ΔABH vuông tại H, ta được:
\(AB^2=AH^2+BH^2\)
\(\Leftrightarrow AB^2=9^2+12^2=225\)
hay AB=15cm
Áp dụng định lí Pytago vào ΔACH vuông tại H, ta được:
\(AC^2=AH^2+HC^2\)
\(\Leftrightarrow AC^2=12^2+16^2=400\)
hay AC=20cm
Vậy: AB=15cm; AC=20cm
Ta có: BH+CH=BC(H nằm giữa B và C)
hay BC=9+16=25cm
Ta có: \(AB^2+AC^2=15^2+20^2=625\)
\(BC^2=25^2=625\)
Do đó: \(BC^2=AB^2+AC^2\)
Xét ΔABC có \(BC^2=AB^2+AC^2\)(cmt)
nên ΔABC vuông tại A(Định lí Pytago đảo)

Câu c. lên lớp 8 thì em có thể dùng đường trung bình dễ hơn nhiều nhé.


Tam giác AHC vuông tại H nên : AC^2 = AH^2 + CH^2 = 12^2 + 16^2 = 400
=> AC = 20 (cm)
Tam giác AHB vuông tại H nên : AB^2 = AH^2 + BH^2
=> BH^2 = AB^2 - AH^2 = 13^2 - 12^2 = 25
=> BH = 5 (cm)
=> BC = BH + HC = 5 + 16 = 21 (cm)
Tk mk nha
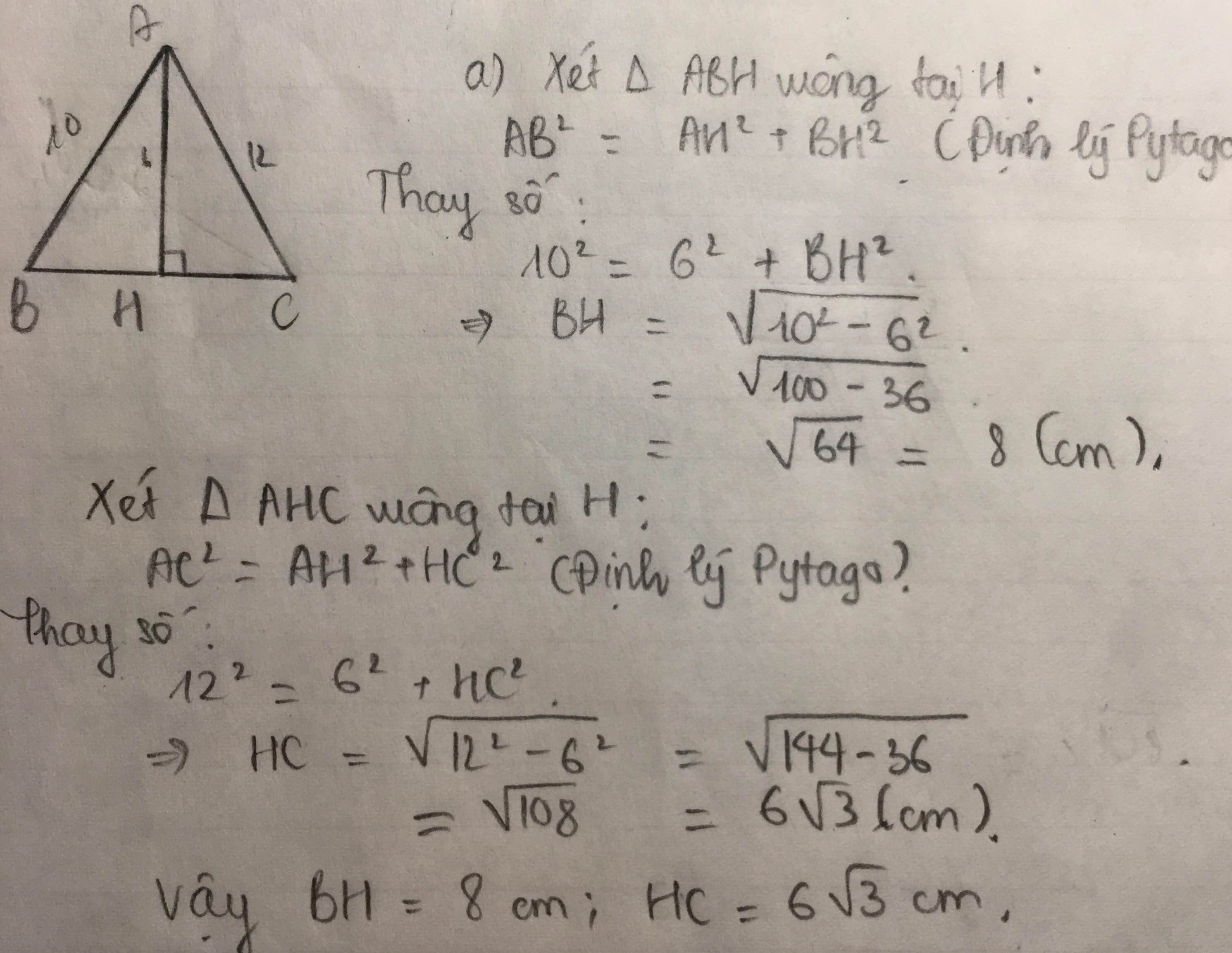
Bài 1 :
A B C H 12 10
Ta có : \(\Delta ABC\) cân tại A (gt)
Mà có : AH là đường cao trong tam giác cân
=> AM đồng thời là đường trung trực trong tam giác cân
=> \(BH=HC\) (tính chất đường trung trực)
Nên có : \(BH=\dfrac{1}{2}BC=\dfrac{1}{2}.10=5\left(cm\right)\)
Xét \(\Delta ABH\) vuông tại H có :
\(AH^2=BH^2+AB^2\) (Định lí PITAGO)
=> \(AH^2=5^2+12^2\)
=> \(AH^2=169\)
=> \(AH=\sqrt{169}=13\left(cm\right)\)
Bài 3 :
A B C 16 13 12
Xét \(\Delta AHC\) vuông tại H có :
\(AC^2=AH^2+HC^2\)
=> \(AC^2=12^2+16^2\)
=> \(AC^2=400\)
=> \(AC=\sqrt{400}=20\)(cm)
Xét \(\Delta AHB\) vuông tại H có :
\(BH^2=AB^2-AH^2\)
=> \(BH^2=13^2-12^2\)
=> \(BH^2=25\)
=> \(BH=\sqrt{25}=5\left(cm\right)\)
Nên ta có : \(BC=BH+HC=5+16=21\left(cm\right)\)