Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Ko hợp lí vì chỉ có 56/100 học sinh lựa chọn
b: Hợp lí

Để khối lượng giấy vụn các lớp khối 8 đã thu gom được, ta chọn biểu đồ cột.
Biểu đồ cột biểu diễn khối lượng giấy vụn các lớp khối 8 đã thu gom được:
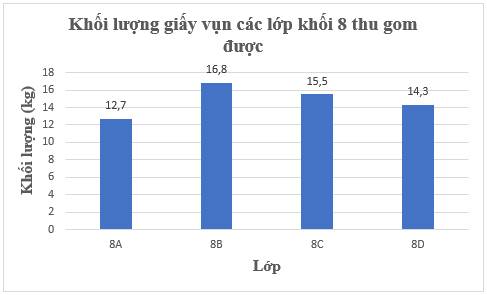

a) Để so sánh số lượng học sinh tham gia hai câu lạc bộ này ở từng lớp, ta chọn biểu đồ cột kép.
Biểu đồ cột kép biểu diễn số lượng của các lớp khối 8 tham gia các câu lạc bộ Thể thao và Nghệ thuật của trường như sau:
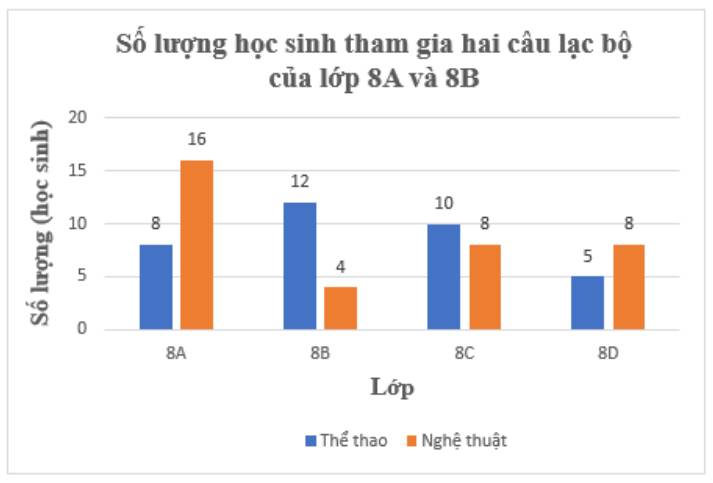
b) Để biểu diễn tỉ lệ học sinh các lớp tham gia hai câu lạc bộ trong số các học sinh khối 8 tham gia hai câu lạc bộ này ta dùng biểu đồ hình quạt tròn.
Tổng số học sinh tham gia hai câu lạc bộ của khối 8 là:
8 + 16 + 12 + 4 + 10 + 8 + 5 + 8 = 71 (học sinh).
• Tổng số học sinh tham gia hai câu lạc bộ của lớp 8A là: 8 + 16 = 24 (học sinh).
Tỉ số phần trăm số học sinh tham gia hai câu lạc bộ của lớp 8A so với số các học sinh khối 8 tham gia hai câu lạc bộ là: \(\frac{{24}}{{71}} \approx 33,8\% \) .
• Tổng số học sinh tham gia hai câu lạc bộ của lớp 8B là: 12 + 4 = 16 (học sinh).
Tỉ số phần trăm số học sinh tham gia hai câu lạc bộ của lớp 8B so với số các học sinh khối 8 tham gia hai câu lạc bộ là: \(\frac{{16}}{{71}} \approx 22,5\% \)
• Tổng số học sinh tham gia hai câu lạc bộ của lớp 8C là: 10 + 8 = 18 (học sinh).
Tỉ số phần trăm số học sinh tham gia hai câu lạc bộ của lớp 8C so với số các học sinh khối 8 tham gia hai câu lạc bộ là: \(\frac{{18}}{{71}} \approx 25,4\% \).
• Tỉ số phần trăm số học sinh tham gia hai câu lạc bộ của lớp 8C so với số các học sinh khối 8 tham gia hai câu lạc bộ là:
100% − 33,8% − 22,5% − 25,4% = 18,3%.
Biểu đồ hình quạt tròn biểu diễn tỉ lệ học sinh các lớp tham gia hai câu lạc bộ trong số các học sinh khối 8 tham gia hai câu lạc bộ này.
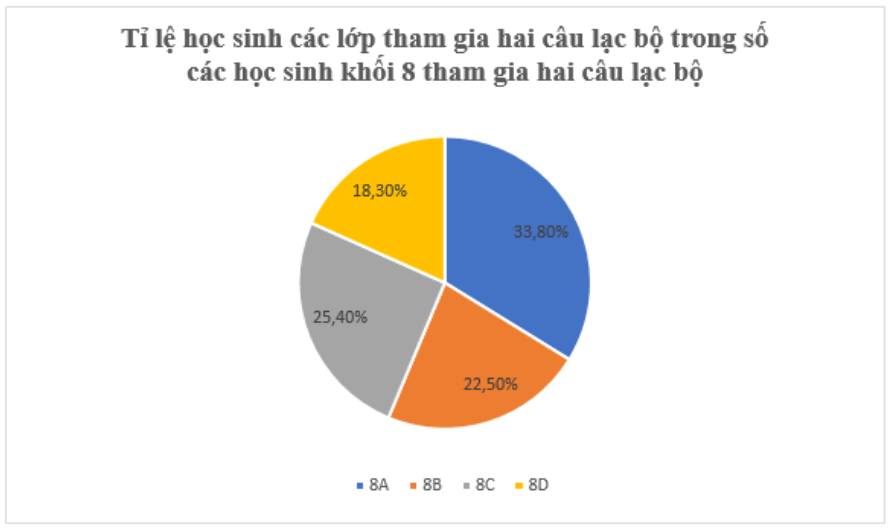

a)
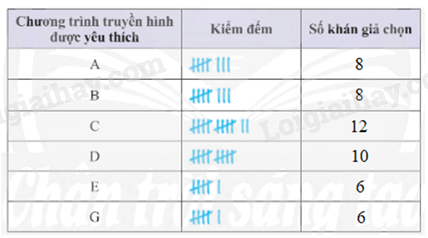
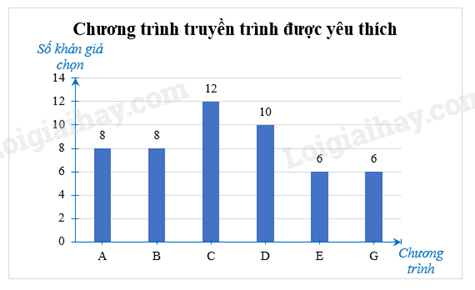
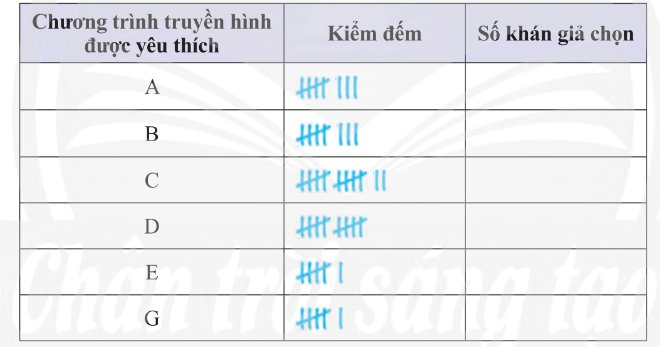
Ta dùng biểu đồ cột để biểu diễn dữ liệu trên.
b) Chương trình truyền hình được yêu thích nhất là chương trình C với số khán giả chọn cao nhất (12 khán giá chọn).
c) Hai cặp chương trình truyền hình được yêu thích ngang nhau là:
• Chương trình A và B (đều có 8 khán giả chọn);
• Chương trình E và G (đều có 6 khán giả chọn).
d) Biểu đồ cột biểu diễn bảng số liệu trên:

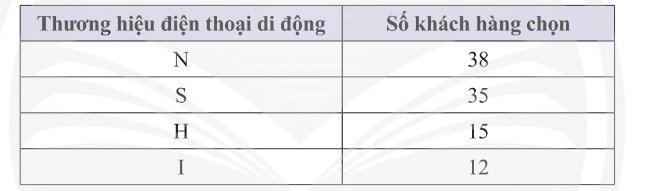
Tổng số điện thoại đã bán ra của cửa hàng:
712 + 1035 + 1085 = 2832 (chiếc)
Xác suất thực nghiệm của biến cố E:
P(E) = 712/2832 = 89/354

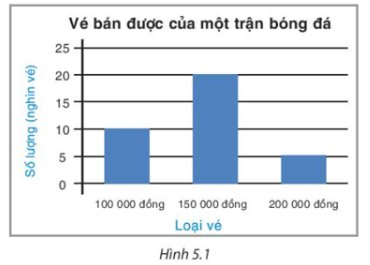
Ta lập bảng thống kê cho dữ liệu được biểu diễn trong biểu đồ trên như sau:
Loại vé | 100 000 đồng | 150 000 đồng | 200 000 đồng |
Số lượng (nghìn vé) | 10 | 20 | 5 |
Để biểu diễn dữ liệu Bảng 5.1, ta nên chọn biểu đồ tranh.
Ta chọn mỗi biểu tượng biểu diễn cho 5 nghìn vé.
Khi đó, số biểu tượng biểu tượng cần biểu diễn số vé 100 000 đồng là:
10 : 5 = 2 (biểu tượng)
Số biểu tượng biểu tượng cần biểu diễn số vé 150 000 đồng là:
20 : 5 = 4 (biểu tượng)
Số biểu tượng biểu tượng cần biểu diễn số vé 200 000 đồng là:
5 : 5 = 1 (biểu tượng)
Ta vẽ biểu đồ tranh như sau:
Loại vé 100 000 đồng | ☺ ☺ |
Loại vé 150 000 đồng | ☺ ☺ ☺ ☺ |
Loại vé 200 000 đồng | ☺ |
(Mỗi ☺ ứng với 5 nghìn vé)

Gọi \(A\) là biến cố người được chọn ngẫu nhiên ủng hộ việc tắt điện trong sự kiện Giờ Trái Đất.
Xác suất thực nghiệm của biến cố \(A\) là \(\frac{{255}}{{300}} = 0,85\).
Do số người chọn lớn nên \(P\left( A \right) \approx 0,85\).
Vậy xác suất của biến cố “Một người được lựa chọn ngẫu nhiên trong khu dân cư ủng hộ việc tắt đèn điện trong sự kiện Giờ Trái Đất” khoảng 0,85.
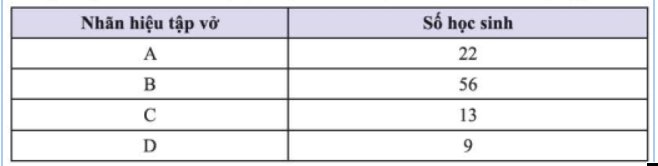


`a, b` đều không hợp lý.