Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1: Thực hiện phép tính:

Bài 2: Tìm x, biết:

Bài 3:
Ba đội máy cày có 18 máy (có cùng năng suất) làm việc trên 3 cánh đồng có cùng diện tích. Đội 1 làm xong trong 3 ngày, đội 2 trong 4 ngày và đội 3 trong 6 ngày. Hỏi mỗi đội có mấy máy?
Bài 4: Cho ABC có AB = AC, M là trung điểm của BC.
a. Chứng minh: ABM = ACM.
b. Trên tia đối của MA lấy D sao cho MD = MA. Chứng minh: AC = BD.
c. Chứng minh: AB // CD.
d. Trên nửa mặt phẳng bờ là AC không chứa B, vẽ tia Ax // BC, lấy IAx sao cho AI = BC. Chứng minh: D, C, I thẳng hàng.

Bài 1 (2đ) a) √25–√494+√0,2525–494+0,25
b) (–2527–3142)–(–727–342)(–2527–3142)–(–727–342)
c) 10310–(9,5–0,25.18):0,5115–11210310–(9,5–0,25.18):0,5115–112
d) 349.192–349.52–(120–14)2.(–12–19314)349.192–349.52–(120–14)2.(–12–19314)
Bài 2 (2đ)
1) Tìm x biết:
a) ∣∣∣12x–16∣∣∣=13|12x–16|=13
b) (4x2–3)3+8=0(4x2–3)3+8=0
2) Vẽ đồ thị hàm sốy=–12xy=–12x. Từ đó chứng minh 3 điểm A(2; -1), B(-12; -6) và C(-2; 1) không thẳng hàng.
Bài 3 (1,5đ) Có ba máy bơm cùng bơm nước vào ba bể có thể tích bằng nhau (lúc đầu các bể đều không có nước). Mỗi giờ máy thứ nhất, máy thứ hai, máy thứ ba bơm được lần lượt là 6m3, 10m3, 9m3. Thời gian bơm đầy bể của máy thứ hai ít hơn máy thứ nhấtlà 2 giờ. Tính thời gian của từng máy để bơm đầy bể.
Bài 4 (3,5đ) Cho tam giác ABC có AB < AC, tia phân giác của góc A cắt cạnh BC tại I. Trên cạnh AC lấy điểm D sao cho AD = AB.
a) Chứng minh rằng BI = ID.
b) Tia DI cắt tia AB tại E. Chứng minh rằng ΔIBE=ΔIDCΔIBE=ΔIDC.
c) Chứng minh BD // EC.
d) Cho ∠ABC=2∠ACB.∠ABC=2∠ACB. Chứng minh rằng AB + BI = AC.
Bài 5 (1đ) a) Cho các số a, b, c, x, y, z thỏa mãn a + b + c = a2 + b2 + c2 = 1 và xa=yb=zcxa=yb=zc (các tỉ số đều có nghĩa). Chứng minh x2 + y2 + z2 = (x + y + z)2.
b) (Dành riêng cho lớp 7A)
Cho tam giác ABC có AB = 2 cm, BC = 4 cm và ˆABCABC^ = 600. Trên tia đối của tia BC lấy điểm D sao cho BD = BC, trên tia đối của tia BA lấy điểm E sao cho BE = BA. Tính diện tích tứ giác ACED.

Bài 1: a)√25–√494+√0,25=√52–√(72)2+√0,52=5–72+0,5=5–3,5+0,5=2.a)25–494+0,25=52–(72)2+0,52=5–72+0,5=5–3,5+0,5=2.
b)(–2527–3142)–(–727–342)=–2527–3142+727+342=(727–2527)+(342–3142)=–1827–2842=–23–23=–43b)(–2527–3142)–(–727–342)=–2527–3142+727+342=(727–2527)+(342–3142)=–1827–2842=–23–23=–43
c)10310–(9,5–0,25.18):0,5115–112=10310–(192–14.18):1265–32=10310–(192–92).26.25.2–3.55.2=10310–102.21210–1510=10310–10–310=10310–10010–310=310–310=–1c)10310–(9,5–0,25.18):0,5115–112=10310–(192–14.18):1265–32=10310–(192–92).26.25.2–3.55.2=10310–102.21210–1510=10310–10–310=10310–10010–310=310–310=–1
d)349.192–349.52–(120–14)2.(–12–19314)=349.(192–52)–(120–1.54.5)2.((–1).72.7–19314)=349.142–(120–520)2.(–714–19314)=37–(–420)2.(–20014)=37–(–15)2.(–1007)=37–125.(–100)7=37+47=77=1d)349.192–349.52–(120–14)2.(–12–19314)=349.(192–52)–(120–1.54.5)2.((–1).72.7–19314)=349.142–(120–520)2.(–714–19314)=37–(–420)2.(–20014)=37–(–15)2.(–1007)=37–125.(–100)7=37+47=77=1
Bài 2:
1) a) – Nếu 12x–16≥012x–16≥0 tứcx≥13x≥13thì∣∣∣12x–16∣∣∣=12x–16|12x–16|=12x–16
Ta có phương trình ⇔12x–16=13⇔12x–16=13
⇔12x=13+16⇔12x=13+16
⇔12x=12⇔12x=12
⇔x=1(tmdkx≥13)⇔x=1(tmdkx≥13)
– Nếu 12x–16<012x–16<0 tức là x <1313thì∣∣∣12x–16∣∣∣=–(12x–16)=16–12x|12x–16|=–(12x–16)=16–12x
Ta có phương trình ⇔16–12x=13⇔16–12x=13
⇔12x=16–13⇔12x=16–13
⇔12x=–16⇔12x=–16
⇔x=–13(tmdkx<13)⇔x=–13(tmdkx<13)
Vậy x = 1 hoặcx=–13.x=–13.
b) (4x2–3)3+8=0⇔(4x2–3)3=–8⇔4x2–3=–2⇔4x2=1⇔x2=14⇔|x|=12⇔⎡⎢ ⎢⎣x=12x=–12.(4x2–3)3+8=0⇔(4x2–3)3=–8⇔4x2–3=–2⇔4x2=1⇔x2=14⇔|x|=12⇔[x=12x=–12.
Vậyx=–12x=–12hoặcx=12x=12.
2) Vẽ đồ thị hàm sốy=–12xy=–12x .
– Khix=–2x=–2thìy=–12.(–2)=1y=–12.(–2)=1.
Vậy điểmC(–2;1)C(–2;1)thuộc đồ thị của hàm số .
Đồ thị của hàm số này là đường thẳng OC trong hình vẽ bên.
– Xét điểm A, B thấy điểm C thuộc đồ thị còn điểm B không thuộc đồ thị , thật vậy:
+ Khi x = –12–12thìy=–12.(–12)=6≠–6y=–12.(–12)=6≠–6nên điểm B(–12;–6–12;–6) không thuộc đồ thị .
+ Khix=2x=2thìy=–12.2=–1y=–12.2=–1nên điểmA(2;–1)A(2;–1)thuộc đồ thị .
Điểm A, C thuộc đồ thị còn điểm B không thuộc đồ thị nên 3 điểm A, B, C không thẳng hàng. (đpcm)
Bài 3: Gọi thời gian của từng máy để bơm đầy bể theo thứ tự làx,y,zx,y,z (giờ)(x,y,z>0).(x,y,z>0).
Vì thể tích 3 bể như nhau, nên thời gian của từng máy để bơm đầy b và thể tích nước bơm được mỗi giờ của mỗi máy là 2 đại lượng tỉ lệ nghịch.
Theo đề bài ta có: 6.x = 10.y = 9.z (1)
và x – y = 2 (2)
Từ (1) ta có: 6x90=10y90=9z906x90=10y90=9z90 (90 làBCNN(6; 10; 9)⇒x15=y9=z10⇒x15=y9=z10 (3)
Theo tính chất của dãy tỉ số bằng nhau, từ (3) và (2) ta có:x15=y9=z10=x–y15–9=26=13x15=y9=z10=x–y15–9=26=13
⇒x=153=5⇒x=153=5giờ, y=93=3y=93=3giờ vàz=103z=103giờ = 3 giờ 20 phút.
Vậy thời gian của từng máy để bơm đầy bể lần lượt là 5 giờ, 3 giờ và 3 giờ 20 phút.
Bài 4:
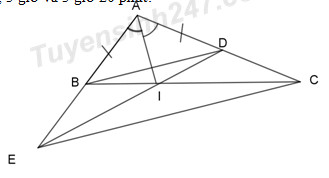
a) Xét tam giác ABI và tam giác ADI ta có:
∠BAI=∠DAI∠BAI=∠DAI (theo giả thiết)
AB=ADAB=AD (theo giả thiết)
AI: chung
⇒ΔABI=ΔADI(c–g–c)⇒ΔABI=ΔADI(c–g–c)
⇒BI=ID⇒BI=ID (2 cạnh tương ứng) (đpcm)
b) VìΔABI=ΔADI(c–g–c)ΔABI=ΔADI(c–g–c)nên:
∠ABI=∠ADI∠ABI=∠ADI (2 góc tương ứng) (1)
Mà: ∠ABE=∠ADC=1800∠ABE=∠ADC=1800 (2 góc bẹt) (2)
Từ (1) và (2) ta có: ∠ABE–∠ABI=∠ADC–∠ADI⇔∠IBE=∠IDC∠ABE–∠ABI=∠ADC–∠ADI⇔∠IBE=∠IDC
XétΔIBEΔIBEvàΔIDCΔIDC ta có:
∠IBE=∠IDC∠IBE=∠IDC (chứng minh trên)
∠BIE=∠DIC∠BIE=∠DIC (2 góc đối đỉnh)
BI=IDBI=ID (chứng minh trên)
⇒ΔIBE=ΔIDC(g–c–g)⇒ΔIBE=ΔIDC(g–c–g) (đpcm)
c) Ta có: BI = ID (chứng minh trên) ⇒ΔBID⇒ΔBIDcân tạiI⇒∠IBD=∠IDBI⇒∠IBD=∠IDB (tính chấtcủa tam giác cân) (1)
Ta lạicó: ΔIBE=ΔIDC(g–c–g)ΔIBE=ΔIDC(g–c–g) (chứng minh trên) ⇒IE=IC⇒IE=IC (2 cạnh tương ứng) ⇒ΔIEC⇒ΔIECcân tại I
⇒∠IEC=∠ICE⇒∠IEC=∠ICE (tính chấtcủa tam giác cân) (2)
Xét 2 tam giácΔIECΔIECvàΔIBDΔIBD ta có:
∠BID=∠EIC∠BID=∠EIC (2 góc đối đỉnh)
∠IBD+∠IDB+∠BID=∠IEC+∠ICE+∠EIC=1800∠IBD+∠IDB+∠BID=∠IEC+∠ICE+∠EIC=1800 (Tổng 3 góc của một tam giác bằng 1800) (3)
Từ (1), (2) và (3) ta có: 2∠IDB+∠BID=2∠IEC+∠EIC2∠IDB+∠BID=2∠IEC+∠EIC
⇒∠IDB=∠IEChay∠EDB=∠DEC⇒∠IDB=∠IEChay∠EDB=∠DEC (cặp góc so le trong bằng nhau)
⇒BD∥EC⇒BD∥EC (đpcm)
d)Ta cóΔIBE=ΔIDC(g–c–g)ΔIBE=ΔIDC(g–c–g)(chứng minh trên)
⇒∠BEI=∠DCI⇒∠BEI=∠DCI (2 góc tương ứng)
Lạicó: ∠BIE=∠DIC∠BIE=∠DIC (2 góc đối đỉnh)
⇒∠BEI+∠BIE=∠DCI+∠DIC⇒∠BEI+∠BIE=∠DCI+∠DIC (*)
Xét tam giác BIE ta có:
∠ABC=∠BIE+∠BEI∠ABC=∠BIE+∠BEI (gócngoàicủa 1 tam giác bằng tổng 2 góc trong không kề với nó) (**)
Từ (*) và (**) ta có: ∠ABC=∠DCI+∠DIC∠ABC=∠DCI+∠DIC hay ∠ABC=∠ACB+∠DIC∠ABC=∠ACB+∠DIC
Theo giảthiết, ta có: ∠ABC=2∠ACB∠ABC=2∠ACB
⇒∠DCI=∠DIC⇒ΔDIC⇒∠DCI=∠DIC⇒ΔDICcântạiD⇒DI=DCD⇒DI=DC.
Vì BI = ID (chứng minh trên) nên BI = DC.
⇒⇒ AC = AD + DC = AB + BI (đpcm)
Bài 5: a) Theo tính chất dãy tỉ số bằng nhau ta có:
xa=yb=zc=x+y+za+b+cxa=yb=zc=x+y+za+b+c=x+y+z1=x+y+z=x+y+z1=x+y+z (Theo giả thiết a + b + c = 1)
⇒(xa)2=(yb)2=(zc)2=(x+y+z)2⇒(xa)2=(yb)2=(zc)2=(x+y+z)2 (1)
Theo tính chất dãy tỉ số bằng nhau, ta lại có:
(xa)2=(yb)2=(zc)2(xa)2=(yb)2=(zc)2=x2+y2+z2a2+b2+c2=x2+y2+z21=x2+y2+z2=x2+y2+z2a2+b2+c2=x2+y2+z21=x2+y2+z2(Theo giả thiếta2+b2+c2=1a2+b2+c2=1) (2)
Từ (1) và (2) ta có: x2+y2+z2=(x+y+z)2(dpcm)x2+y2+z2=(x+y+z)2(dpcm)
b) XétΔABCΔABCvàΔEBDΔEBD ta có:
AB = EB (theo gt)
BD = BC (theo gt)
∠ABC=∠EBD∠ABC=∠EBD (cặp gócđối đỉnh bằng nhau)
⇒ΔABC=ΔEBD(c–g–c)⇒ΔABC=ΔEBD(c–g–c)
Chứng minh tươngtự ta có: ΔABD=ΔEBC(c–g–c)ΔABD=ΔEBC(c–g–c)
⇒SΔABC+SΔABD=SΔEBD+SΔEBC⇒SΔABC+SΔABD=SΔEBD+SΔEBC⇒SΔEDC=SΔACD=12SACED⇒SΔEDC=SΔACD=12SACED
Kẻ đường cao AH của tam giác ACD (H∈DCH∈DC)
Xét tam giác vuông AHB ta có:
∠BAH+∠ABH=900⇔∠BAH+600=900⇔∠BAH=300∠BAH+∠ABH=900⇔∠BAH+600=900⇔∠BAH=300
⇒BH=12AB=12.2=1cm⇒BH=12AB=12.2=1cm(Tam giác vuông có một góc bằng 30000000 thì cạnh đối diện góc đó bằng nửa cạnh huyền)
Áp dụng định lý Pitago vào tam giác vuông AHB, ta có:
AH2+BH2=AB2⇔AH2+12=22AH2+BH2=AB2⇔AH2+12=22
⇔AH2=4–1=3⇔AH=√3cm⇔AH2=4–1=3⇔AH=3cm
Vậy diện tích tứ giác ACED là: SACED=2.SΔACDSACED=2.SΔACD=2.12.AH.DC=AH.2BC=√3.2.4=8√3cm
đề Anh
I am a student. So I spend the day in a (1) _________ way. I get up from bed (2) _________ in the morning. First, I do my morning (3) _________ I wash my face and (4) _________ my teeth. I take great care of my teeth, because bad teeth are a sign of bad (5) _________. Then I take a little (6) _________ exercise. After taking exercise, I go out for a walk in the open (7) _________. There I breathe (8) _________ morning air. My mind and body are both (9) _________ . Then I return home. I say my short (10) _________.
II. Choose the word whose underlined part is pronounced differently.
Question 11.
A. come B. money
C. notebook D. Monday
Question 12.
A. couple B. though
C. soul D. elbow
Question 13.
A. seven B. vowel
C. very D. foot
III. Choose the odd one out.
Question 14.
A. friend B. parent
C. uncle D. aunt
Question 15.
A. small B. big
C. old D. meet
Question 16.
A. school B. classmate
C. theater D. market
IV. Choose A, B, C or D that best completes the sentences or substitutes for the underlined word or phrase.
Question 17. Do volunteers often spend time helping other people in ___________, orphanages or homes for the aged.
A. capitals B. markets
C. schools D. hospitals
Question 18. we are helping the poor people in the remote areas.
A. faraway B. nearby
C. small D. difficult
Question 19. During summer vacations, we teach children in ___________ areas how to read and write.
A. mountain B. urban
C. mountainous D. suburb
Question 20. What kind of ___________ work are you paripating in?
A. voluntarily B. volunteer
C. voluntary D. volunteerism
Question 21. People who are not in good health are ___________ people.
A. elderly B. homeless
C. rich D. sick
Question 22. I was absent ___________ class yesterday.
A. in B. of
C. from D. at
Question 23. He was delighted ___________ the present you gave him.
A. in B. to
C. for D. with
Question 24. It is very kind ___________ you to help them.
A. of B. in
C. about D. to
Question 25. It is difficult ___________ handicapped children to study with other children.
A. to B. for
C. on D. from
Question 26. I’m very grateful ___________ her for her help.
A. on B. of
C. about D. to
V. Read the text and choose the correct answer A, B, C, or D for each of the gaps.
EARTHWATCH
Have you ever wanted to do something different? Five years ago, Will Slade read about (27) ______ organization called Earthwatch. Earthwatch finds volunteers (28) ______ expeditons (29) ______ and explore different parts of the world.
Will decided (30) ______ an expedition to study elephants in Africa. “I wasn’t sure about it before I went.” say Will. “But in fact, I really enjoyed every minute of the expedition. We slept (31) ______ tents and we cooked our own food, but it was the great (32) ______ elephants and all the other animals there”. “I’ve (33) ______ all the expeditions, and I have seen some fantas places. How (34) ______ people have slept (35) ______ a beach, climbed a mountain, or see a whale? This world is such a beautiful place, but it’s disappearing fast. We have to learn more (36) ______ it if we are going to save it.”
Question 27.
A. a B. the
C. an D. some
Question 28.
A. to B. for
C. at D. on
Question 29.
A. studying B. studied
C. study D. to study
Question 30.
A. to join B. join
C. joining D. joined
Question 31.
A. on B. in
C. at D. under
Question 32.
A. see B. saw
C. seeing D. to see
Question 33.
A. enjoyed B. enjoy
C. enjoying D. to enjoy
Question 34.
A. much B. far
C. many D. long
Question 35.
A. in B. on
C. to D. above
Question 36.
A. at B. in
C. of D. about
VI. Choose the best sentence that can be made from the cues given.
Question 37. I / not / visited / museum / three months.
A. I haven’t visited the museum three months ago.
B. I havn’t visited the museum for three months.
C. I didn’t visited the museum for three months.
D. I haven’t visited the museum three months ago.
Question 38. Ms Linda / beautiful photos / few days ago.
A. Ms Linda took many beautiful photos a few days ago.
B. Ms Linda took much beautiful photos a few days ago.
C. Ms Linda took many beautiful photos few days ago.
D. Ms Linda took much beautiful photos few days ago.
Question 39. The students / arrived / because / traffic jam.
A. The students arrived late because the traffic jam.
B. The students arrived late because of the traffic jam.
C. The students arrived lately because the traffic jam.
D. The students arrived lately because of the traffic jam.
Question 40. I / eat / fruits / because / they / green.
A. I can’t eat these fruits because of they are green.
B. I can’t eat this fruits because of they are green.
C. I can’t eat these fruits because they are green.
D. I can’t eat this fruits because they are green.

Question 1. simple
Question 2. early
Question 3. duties
Question 4. brush
Question 5. health
Question 6. physical
Question 7. field
Question 8. pure
Question 9. refreshed
Question 10. prayer
| Question 11. C | Question 26. D |
| Question 12. A | Question 27. C |
| Question 13. D | Question 28. B |
| Question 14. A | Question 29. D |
| Question 15. D | Question 30. A |
| Question 16. B | Question 31. B |
| Question 17. D | Question 32. D |
| Question 18. A | Question 33. A |
| Question 19. C | Question 34. C |
| Question 20. C | Question 35. B |
| Question 21. D | Question 36. D |
| Question 22. C | Question 37. B |
| Question 23. D | Question 38. A |
| Question 24. A | Question 39. B |
| Question 25. B | Question 40. C |

https://dethi.violet.vn/category/toan-7-1179.html
#Châu's ngốc

HỌC KÌ 1
Bài 1. Cho tam giác ABC, có góc A = 90º, d là đường thẳng qua C và vuông góc với BC; tia phân giác của góc B cắt AC ở D và cắt d ở E. Kẻ CH vuông góc với DE, H thuộc DE. Chứng minh CH là tia phân giác của góc DCE?
Bài 2: Cho tam giác ABC, góc B > góc C, AD là tia phân giác
a) Chứng minh góc ADC - ADB = góc B - C
b) Phân giác góc ngoài tại A của tam giác ABC cắt BC ở E. Chứng minh góc AEB = 1/2 (B -C)
Bài 3: Cho tam giác ABC, gọi D, E lần lượt là trung điểm của AC, AB. Trên tia đối của tia DB lấy M sao cho DM = DB; trên tia đối của tia EC lấy N sao cho EN = EC. Chứng minh A là trung điểm của MN?
Bài 4: Cho tam giác ABC có góc A = 50°. Vẽ đoạn thẳng AI vuông góc và bằng AB (I và C khác phía với AB). Vẽ đoạn thẳng AK vuong góc và bằng AC (K và B khác phía với AC). Chứng minh:
a) IC = BK
b) IC vuông góc BK
Bài 5: Cho tam giác ABC có góc A = 100°, M là trung điểm của BC, trên tia đối của MA lấy K sao cho MK = MA
a) Tính số đo góc ABK?
b) Ở phía ngoài tam giác ABC, vẽ AD vuông góc và bằng AB, AE vuông góc và bằng AC. Chứng minh hai tam giác ABK và DAE bằng nhau
c) Chứng minh MA vuông góc DE
Bài 6: Cho tam giác ABC có tia phân giác của góc ABC cắt cạnh AC ở D, tia phân giác của góc ACB cắt cạnh AB ở E. Biết BE + CD = BC. Tính số đo góc BAC?
Bài 7: Cho tam giác ABC có góc B = 2C. Tia phân giác của góc B cắt AC ở D. Trên tia đối của BD lấy E sao cho BE = AC. Trên tia đối của CB lấy K sao cho CK = AB. Chứng minh AE = AK.
Bài 8: Cho tam giác ABC, D là trung điểm của AB, E là trung điểm của AC. Vẽ F sao cho E là trung điểm của DF. Chứng minh:
a) DB = CF
b) Hai tam giác BDC và FCD bằng nhau
c) DE // BC và DE = 1/2BC
Bài 9: Cho tam giác ABC. Trên AB lấy D à E sao cho AD = BE. Qua D, E vẽ các đường thẳng song song với BC, chúng cắt AC theo thứ tự ở M và N. Chứng minh BC = DM + EN.
Bài 10: Cho tam giác ABC có góc A = 600. Các tia phân giác của các góc B và C cắt nhau ở I và cắt AC, AB theo thứ tự ở D và E. Chứng minh ID = IE.
Bài 11: Cho tam giác ABC vuông tại A có AB = AC. Lấy D thuộc AB, E thuộc AC sao cho AD = AE. Đường thẳng đi qua D vuông góc với BE cắt CA ở K. Chứng minh AK = AC?
Bài 12: Cho tam giác ABC có góc A nhọn, AB = AC. Qua A kẻ đường thẳng xy sao cho B và C nằm cùng phía với xy. Vẽ BD vuông góc xy ở D, CE vuông góc xy ở E.
a) Chứng minh hai tam giác BAD và ACE bằng nhau.
b) Chứng minh DE = BD + CE
Bài 13: Cho tam giác ABC có góc A nhọn. Trên nửa mặt phẳng bờ AB chứ C, vẽ AD vuông góc với AB, AD = AB. Trên nửa mặt phẳng bờ AC chứa B, vẽ AE vuông góc AC, AE = AC. Kẻ AH vuông góc ED tại H. Chứng minh AH đi qua trung điểm của BC?
Bài 14: Gọi D là trung điểm cạnh BC của tam giác ABC. Qua D kẻ đường thẳng vuông góc với đường phân giác trong của góc BAC cắt AB, AC lần lượt ở M và N.
a) Chứng minh BM = CN
b) Cho biết AB = c, AC = b. Tính độ dài các đoạn thẳng AM, BM.
Bài 15: Cho tam giác ABC có AB = AC, M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao cho AM = MD
a. Chứng minh rằng tam giác ABM bằng tam giác DCM.
b. Chứng minh AB song song với DC.
c. Chứng minh AM vuông góc với BC.
Bài 16: Cho tam giác ABC vuông tại A, AB = AC. Qua A vẽ đường thẳng d sao cho B nằm cùng phía đối với đường thẳng d. Kẻ BH và CK vuông góc với d. Chứng minh:
a. AH = CK
b. HK = BH + CK
Bài 17: Cho góc nhon xOy. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OB = OA. Trên tia Ax lấy điểm C, trên tia By lấy điểm D sao cho AC = BD
a. Chứng minh AD = BC
b. Gọi E là giao điểm của AD và BC. Chứng minh tam giác EAC bằng tam giác EBD
c. Chứng minh OE là phân giác góc xOy
Bài 18: Cho tam giác ABC có 3 góc đều nhọn, đường cao AH vuông góc với BC tại H. Trên tia đối của tia HA lấy điểm D sao cho HA = HD
a. Chứng minh BC và CB lần lượt là tia phân giác của các góc ABD và ACD.
b. Chứng minh CA = CD và DB = BA
c. Cho góc ACB bằng 45o tính góc ADC.
HỌC KÌ 2
Bài 1 :
Cho tam giác ABC vuông tại A. đường phân giác BE. Kẻ EH vuông góc với BC. gọi K là giao điểm của AB và HE. Chứng minh rằng:
a) ΔABE = ΔHBE
b) BE là đường trung trực của AH.
c) EK = EC.
d) AE < EC
Bài 2 : Cho tam giác ABC vuông tại A (AB < AC).Trên tia đối của tia AC lấy điểm D sao cho AD = AB. Trên tia đối của tia AB lấy điểm E sao cho AE = AC.
a) Chứng minh: BC = DE.
b) Chứng minh: tam giác ABD vuông cân và BD // CE.
c) Kẻ đường cao AH của tam giác ABC tia AH cắt cạnh DE tại M. từ A kẻ đường vuông góc CM tại K, đường thẳng này cắt BC tại N . Chứng minh: NM // AB.
d) Chứng minh: AM = DE/2.
Bài 3: Cho tam giác ABC vuông tại A có. Vẽ AK vuông góc BC (K thuộc BC). Trên tia đối của tia KA lấy điểm M sao cho KA = KM
a) Chứng minh: DKAB = DKMB. Tính số đo góc MAB
b) Trên tia KB lấy điểm D sao cho KD = KC. Tia MD cắt AB tại N. Chứng minh: MN vuông góc AB
c) So sánh MD + DB với AB
Bài 4: Cho ΔABC vuông taï A và góc C = 30°.Trên cạnh BC lấy điểm D sao cho BD = BA .
a/ Chứng minh: ΔABD đều, tính góc DAC.
b/ Vẽ DE vuông góc AC (E thuộc AC). Chứng minh: ΔADE = ΔCDE .
c/ Cho AB = 5cm. Tính BC và AC.
d/ Vẽ AH vuông góc BC (H thuộc BC). Chứng minh: AH + BC > AB +AC
Bài 5: Cho ABC cân tại A (A < 90°). Vẽ tia phân giác AH của góc BAC (H thuộc BC); biết AB = 15cm, BH = 9cm.
a) CMR: Δ ABH = Δ ACH
b) Vẽ trung tuyến BD, BD cắt AH tại G. Chứng minh: G là trọng tâm của ABC. Tính AG.
c) Qua H vẽ đường thẳng song song với AC cắt AB tại E. Chứng minh: 3 điểm A; G; E thẳng hàng.
Bài 6: Cho tam giác ABC cân tại A. Trên tia đối của BC lấy điểm M , trên tia đối của CB lấy N sao cho BM = CN , Vẽ BD vuông góc AM tại D, CE vuông góc AN tại E. Cho biết AB = 10 cm, BH = 6 cm. Tính độ dài đoạn AH
a) Chứng minh: Tam giác AMN cân.
b) Chứng minh: DB = CE
c) Gọi K là giao điểm của DB và EC. Chứng minh ΔADK = ΔAEK.
d) Chứng minh KD + KE < 2KA .
Bài 7: Cho ΔABC đều có cạnh 10cm. Từ A dựng tia Ay vuông góc với AB cắt BC tại M.
a/ Chứng minh: ΔACM cân.
b/ Kẻ AH vuông góc BC ( H thuộc BC), lấy điểm I thuộc AH. Biết AB < AM, chứng minh: IB < IM
c/ Kẻ CN vuông góc AM (N thuộc AM), nối HN. Chứng minh: ΔAHN đều
d/ Tính độ dài đoạn thẳng HN.
Bài 8: Cho ΔABC vuông tại A. Trên nửa mặt phẳng có bờ BE không chứa điểm A. Vẽ Bx sao cho góc ABC = góc CBx. Gọi K là giao điểm Bx và AC. Kẻ CH vuông góc Bx. Gọi N là giao điểm CH và AB
a) Chứng minh: Δ HBC = Δ ABC
b) Chứng minh BC là đường trung trực AH
c) Chứng minh CN = CK
d) Chứng minh CK > CA
Bài 9: Cho ΔABC vuông tại A có AB = 6cm; AC = 8cm. Vẽ trung tuyến AM.
a) Tính độ dài AM.
b) Trên tia đối của tia MA lấy điểm D sao cho MD = MA. Chứng minh: ΔAMB = ΔDMC
c) Chứng minh: AC vuông góc DC
d) Chứng minh: AM < (AB + AC ) : 2
Bài 10: Tam giác ABC vuông tại A; phân giác BD. Kẻ DE vuông góc BC (E thuộc BC). Gọi F là giao điểm của BA và ED. Chứng minh:
a) BD là đường trung trực của AE
b) DF = DC
c) AD < DC
Bài 11 : Cho tam giác vuông tại A, đường trung tuyến AM. Trên tia đối của tia MA lấy điểm D sao cho MD = MA.
a) Tính số đo góc ABD.
b) Chứng minh rằng tam giác ABC bằng tam giác BAD.
c) So sánh độ dài AM và BC.

MAI VŨ XUÂN MY:
a) Xét tam giác ABD và tam giác EBD có:
góc A = góc E ( =90độ)
BD = BD (Cạnh chung)
góc B1=-góc B2 (phân giác)
Vậy tam giác ABD = tam giác EBD (chgn)
b) Ta có: tam giác ABD = tam giác EBD (cm a)
=> AB = AE (cạnh tương ứng)
=> tam giác ABE cân tại B
Mà góc B = 60 độ
=> góc A = góc E = \(\frac{180^0-60^0}{2}\)=60 độ
Vậy tam giác ABE là tam giác đều
c) BC=7cm
