Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

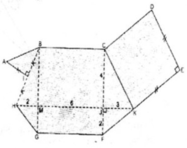
Chia đa giác đó thành hình vuông CDEK, hình thang KFGH, hình thang BCKH và tam giác vuông AIB
Ta có: MJ = KH – KJ – MH = 11 – 2 – 3 = 6(cm)
⇒ BC = GF = MJ = 6 (cm)
CJ = CF – FG = 6 – 2 = 4 (cm)
S K F G H = (HK + GF)/2. FJ = (11 + 6)/2.2 = 17 ( c m 2 )
S B C K H = (BC + KH)/2. FJ = (11 + 6)/2.4 = 34 ( c m 2 )
Trong tam giác vuông BMH có ∠ J = 90 0 .Theo định lý Pi-ta-go ta có:
C K 2 = C J 2 + J K 2 = 16 + 9 = 25 ⇒ CK = 5 (cm)
S C D E K = C K 2 = 5 2 = 25 ( c m 2 )
Trong tam giác vuông BMH có ∠ M = 90 0 .Theo định lý Pi-ta-go ta có:
B H 2 = B M 2 + H M 2
mà BM = CJ = 4(cm) (đường cao hình thang BCKH)
⇒ B H 2 = 4 2 + 2 2 = 20
IB = BH/2 ⇒ I B 2 = B H 2 / 2 = 20/4 = 5
IB = 5 (cm)
∆ AIB vuông cân tại I (vì AI = IH = IB)
S A I B = 1/2 AI. IB = 1/2 I B 2 = 5/2 ( c m 2 )
S = S C D E K + S K F G H + S B C K H + S A I B = 25 + 17 + 34 + 5/2 = 157/2 ( c m 2 )

Bài giải:
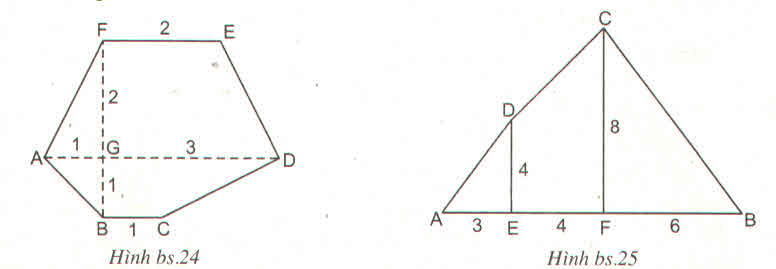
SADEF=\(\dfrac{\left(AD+EF\right).FG}{2}=\dfrac{\left(4+2\right).2}{2}=6\left(cm^2\right)\)
SABCD=\(\dfrac{\left(AD+BC\right).BG}{2}=\dfrac{\left(4+1\right).1}{2}=2,5\left(cm^2\right)\)
=> SABCDEF= SADEF+SABCD= 6+2,5=8,5(cm2)
b) SDEA=\(\dfrac{DE.AE}{2}=\dfrac{4.3}{2}=6\left(cm^2\right)\)
SDCFE=\(\dfrac{\left(DE+CF\right).EF}{2}=\dfrac{\left(4+8\right).4}{2}=24\left(cm^2\right)\)
SCFB=\(\dfrac{CF.FB}{2}=\dfrac{8.6}{2}=24\left(cm^2\right)\)
=> SABCD=SDEA+SDCFE+SCFB=6+24+24=54(cm2)
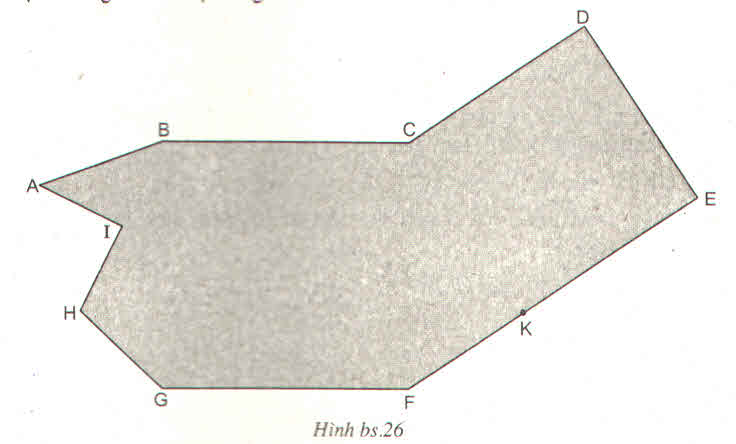


Chia đa giác đó thành hình vuông CDEK, hình thang KFGH, hình thang BCKH và tam giác vuông AIB
Ta có: MJ = KH – KJ – MH = 11 – 2 – 3 = 6(cm)
⇒ BC = GF = MJ = 6 (cm)
CJ = CF – FG = 6 – 2 = 4 (cm)
SKFGH=HK+GF2.FJ=11+62.2=17(cm2)SBCKH=BC+KH2.CJ=11+62.4=34(cm2)SKFGH=HK+GF2.FJ=11+62.2=17(cm2)SBCKH=BC+KH2.CJ=11+62.4=34(cm2)
Trong tam giác vuông CJK có ˆJ=90∘J^=90∘. Theo định lý Pi-ta-go ta có:
CK2=CJ2+JK2=16+9=25⇒CK=5CK2=CJ2+JK2=16+9=25⇒CK=5 (cm)
SCDEK=CK2=52=25SCDEK=CK2=52=25 (cm2 )
Trong tam giác vuông BMH có ˆM=90∘M^=90∘.Theo định lý Pi-ta-go ta có:
BH2=BM2+HM2BH2=BM2+HM2
mà BM = CJ = 4(cm) (đường cao hình thang BCKH)
⇒BH2=42+22=20IB=BH2⇒IB2=BH24=204=5IB=√5(cm)⇒BH2=42+22=20IB=BH2⇒IB2=BH24=204=5IB=5(cm)
∆ AIB vuông cân tại I (vì AI = IH = IB)
SAIB=12AI.IB=12IB2=52SAIB=12AI.IB=12IB2=52 ( cm2 )
S=SCDEK+SKFGH+SBCKH+SAIB=25+17+34+52=1572S=SCDEK+SKFGH+SBCKH+SAIB=25+17+34+52=1572 (cm2 )