Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1. Tính số lần lặp của vòng lặp bên trong của thuật toán sắp xếp chèn tuyến tính.

2. Tính số lần lặp của vòng lặp ngoài của thuật toán sắp xếp chèn tuyến tính.
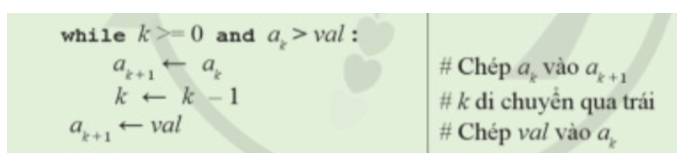
3. Ước lượng độ phức tạp thời gian của thuật toán sắp xếp chèn tuyến tính:
Vòng lặp for bên ngoài kiểm soát việc thực hiện đúng n-1 bước.
Vòng lặp while lồng bên trong thực hiện đồng thời cùng lúc hai việc a) và b) theo cách dịch chuyển dần từng bước sang trái, từ vị trí i tới vị trí k+1

THAM KHẢO!
Một ý tưởng khác để kiểm tra xem dãy n số có phải là một hoán vị của dãy số 1, 2, ..., n hay không là sử dụng tính chất đặc biệt của hoán vị. Ta biết rằng một hoán vị của dãy số từ 1 đến n sẽ có các giá trị từ 1 đến n đúng một lần, tức là không có giá trị lặp lại và không có giá trị bỏ sót. Với ý tưởng này, ta có thể thiết kế thuật toán như sau:
-Đọc dãy số vào mảng a gồm n phần tử.
-Kiểm tra độ dài của dãy a có bằng n không. Nếu không bằng n, in ra "KHÔNG" và kết thúc thuật toán.
-Khởi tạo một mảng visited gồm n phần tử, với giá trị ban đầu là False. Mảng visited này sẽ được sử dụng để đánh dấu các số đã xuất hiện trong dãy a.
-Duyệt qua từng phần tử trong dãy a, đồng thời đánh dấu số đó đã xuất hiện trong dãy a bằng cách đặt giá trị True tại vị trí tương ứng trong mảng visited.
-Kiểm tra mảng visited. Nếu một trong các phần tử của visited là False, tức là có giá trị bị bỏ sót trong dãy a, in ra "KHÔNG" và kết thúc thuật toán.
-Sau khi kiểm tra xong mảng visited, in ra "CÓ" nếu không có giá trị nào bị bỏ sót, ngược lại in ra "KHÔNG".
-Thuật toán:
function kiemTraHoanVi(a):
n = len(a)
visited = [False] * n
# Kiểm tra độ dài của dãy a
if n != len(set(a)):
return "KHÔNG"
# Duyệt qua từng phần tử trong dãy a
for i in a:
# Nếu số i đã xuất hiện trong dãy a
if i < 1 or i > n or visited[i-1]:
return "KHÔNG"
visited[i-1] = True
# Kiểm tra mảng visited
if all(visited):
return "CÓ"
else:
return "KHÔNG"

Thuật toán tìm kiếm nhị phân thực hiện tìm kiếm một mảng đã sắp xếp bằng cách liên tục chia các khoảng tìm kiếm thành 1 nửa. Bắt đầu với một khoảng từ phần tử đầu mảng, tới cuối mảng. Nếu giá trị của phần tử cần tìm nhỏ hơn giá trị của phần từ nằm ở giữa khoảng thì thu hẹp phạm vi tìm kiếm từ đầu mảng tới giửa mảng và nguợc lại. Cứ thế tiếp tục chia phạm vi thành các nửa cho dến khi tìm thấy hoặc đã duyệt hết.
Thuật toán tìm kiếm nhị phân tỏ ra tối ưu hơn so với tìm kiếm tuyết tính ở các mảng có độ dài lớn và đã được sắp xếp. Ngược lại, tìm kiếm tuyến tính sẽ tỏ ra hiệu quả hơn khi triển khai trên các mảng nhỏ và chưa được sắp xếp.

1.Thuật toán tìm kiếm tuần tự:
- Độ phức tạp thời gian của thuật toán tìm kiếm tuần tự là O(n)
- Giá trị lớn nhất của n với thời gian thực thi là 1 giây: n = 1 giây * (106 us / phép tính) = 106
- Giá trị lớn nhất của n với thời gian thực thi là 1 phút: n = 1 phút * (60 giây / phút) * (106us / phép tính) = 6 * 107
- Giá trị lớn nhất của n với thời gian thực thi là 1 giờ: n = 1 giờ * (60 phút / giờ) * (60 giây / phút) * (106us / phép tính) = 3.6 * 109
2.Thuật toán sắp xếp chèn:
- Độ phức tạp thời gian của thuật toán sắp xếp chèn là O(102
- Giá trị lớn nhất của n với thời gian thực thi là 1 giây: n = sqrt(1 giây * (106us / phép tính)) =103
- Giá trị lớn nhất của n với thời gian thực thi là 1 phút: n = sqrt(1 phút * (60 giây / phút) * (106us / phép tính)) = 6 * 104
- Giá trị lớn nhất của n với thời gian thực thi là 1 giờ: n = sqrt(1 giờ * (60 phút / giờ) * (60 giây / phút) * (106us / phép tính)) = 3.6 * 106
3. Thuật toán sắp xếp chọn:
- Độ phức tạp thời gian của thuật toán sắp xếp chọn là O(n2)
- Giá trị lớn nhất của n là: n = sqrt(1 giây * (106us / phép tính)) = 1000.
Thời gian thực thi là 1 phút:
Giá trị lớn nhất của n là: n = sqrt(1 phút * (60 giây / phút) * (106us / phép tính)) = 60000.
Thời gian thực thi là 1 giờ:
Giá trị lớn nhất của n là: n = sqrt(1 giờ * (60 phút / giờ) * (60 giây / phút) * (106us / phép tính)) = 3.6 * 106
gốc: https://codeforces.com/problemset/problem/1558/F