Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a,2x\left(x-3\right)+5\left(x-3\right)=0\)
\(\Leftrightarrow\left(2x+5\right)\left(x-3\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}2x+5=0\\x-3=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}2x=-5\\x=3\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=-\frac{5}{2}\\x=3\end{cases}}\)
Vậy .........
\(b,\left(x^2-4\right)+\left(x-2\right)\left(3-2x=0\right)\)
\(\Leftrightarrow x^2-4-2x^2+7x-6=0\)
\(\Leftrightarrow-x^2+7x-10=0\)
\(\Leftrightarrow-\left(x-5\right)\left(x-2\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=5\\x=2\end{cases}}\)
Vậy ..................
\(c,x^3-3x^2+3x-1=0\)
\(\Leftrightarrow\left(x-1\right)^3=0\)
\(\Leftrightarrow x=1\)
\(d,x\left(2x-7\right)-4x+14=0\)
\(\Leftrightarrow2x^2-7x-4x+14=0\)
\(\Leftrightarrow2x^2-11x+14=0\)
\(\Leftrightarrow\left(2x-7\right)\left(x-2\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=\frac{7}{2}\\x=2\end{cases}}\)
Vậy ............
\(e,\left(2x-5\right)^2-\left(x+2\right)^2=0\)
\(\Leftrightarrow4x^2-20x+25-x^2-4x-4=0\)
\(\Leftrightarrow3x^2-24x+21=0\)
\(\Leftrightarrow3\left(x-7\right)\left(x-1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-7=0\\x-1=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=7\\x=1\end{cases}}\)
Vậy .....................
\(f,x^2-x-\left(3x-3\right)=0\)
\(\Leftrightarrow x^2-x-3x+3=0\)
\(\Leftrightarrow x^2-4x+3=0\)
\(\Leftrightarrow\left(x-3\right)\left(x-1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-3=0\\x-1=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=3\\x=1\end{cases}}\)
Vậy ..............

a)\(\left(x^2+1\right)\left(x^2-4x+4\right)=0\Leftrightarrow\orbr{\begin{cases}x^2+1=0\\x^2-4x+4=0\end{cases}\Rightarrow\orbr{\begin{cases}x^2=-1\left(vn\right)\\\left(x-2\right)^2=0\end{cases}\Rightarrow}x=2}\)
b)\(\left(3x-2\right)\left(\frac{2x+6}{7}-\frac{4x-3}{5}\right)=0\\ \Rightarrow\left(3x-2\right)\left(\frac{10x+30-28x+21}{35}\right)=0\)
\(\Rightarrow\left(3x-2\right)\left(\frac{-18x+51}{35}\right)=0\Rightarrow\orbr{\begin{cases}x=\frac{2}{3}\\x=\frac{17}{6}\end{cases}}\)
c)\(\left(3,3-11x\right)\left(\frac{21x+6+10-30x}{15}\right)=0\Leftrightarrow\orbr{\begin{cases}x=\frac{3}{10}\\x=\frac{16}{9}\end{cases}}\)

a) \(x^4+2x^3-3x^2-8x-4=0\)
\(\Leftrightarrow x^4-2x^3+4x^3-8x^2+5x^2-10x+2x-4=0\)
\(\Leftrightarrow x^3\left(x-2\right)+4x^2\left(x-2\right)+5x\left(x-2\right)+2\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x^3+4x^2+5x+2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x^3+x^2+3x^2+3x+2x+2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left[x^2\left(x+1\right)+3x\left(x+1\right)+2\left(x+1\right)\right]=0\)
\(\Leftrightarrow\left(x-2\right)\left(x+1\right)\left(x^2+3x+2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x+1\right)\left(x^2+2x+x+2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x+1\right)\left[x\left(x+2\right)+\left(x+2\right)\right]=0\)
\(\Leftrightarrow\left(x-2\right)\left(x+1\right)\left(x+2\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x+1\right)^2\left(x+2\right)=0\)
\(\Rightarrow x\in\left\{2;-1;-2\right\}\)
Vậy....
c, \(2x^3+7x^2+7x+2=0\)
\(\Leftrightarrow2\left(x^3+1\right)+7x\left(x+1\right)=0\Leftrightarrow2\left(x+1\right)\left(x^2-x+1\right)+7x\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left[2\left(x^2-x+1\right)+7x\right]=0\)
\(\Leftrightarrow\left(x+1\right)\left(2x^2+5x+2\right)=0\Leftrightarrow\left(x+1\right)\left(x+2\right)\left(2x+1\right)=0\)
Tập nghiệm của pt: \(S=\left\{-1;-2;-\frac{1}{2}\right\}\)
b, \(\left(x-2\right)\left(x+2\right)\left(x^2-10\right)=72\Leftrightarrow\left(x^2-4\right)\left(x^2-10\right)=72\) (1)
Đặt: \(x^2-7=t\left(t\ge-7\right)\)
Khi đó (1) trở thành: \(\left(t+3\right)\left(t-3\right)=72\Leftrightarrow t^2-9=72\Leftrightarrow\orbr{\begin{cases}t=9\\t=-9\left(loai\right)\end{cases}}\)
\(t=9\Rightarrow x^2-7=9\Leftrightarrow x=\pm4\)
Tập nghiệm của pt là \(S=\left\{\pm4\right\}\)
a, \(x^4+2x^3-3x^2-8x-4=0\)
\(\Leftrightarrow x^3\left(x+1\right)+x^2\left(x+1\right)-4x\left(x+1\right)-4\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^3+x^2-4x-4\right)=0\)
\(\Leftrightarrow\left(x+1\right)^2\left(x^2-4\right)=0\Leftrightarrow\orbr{\begin{cases}x=-1\\x=\pm2\end{cases}}\)

chẳng ai giải, thôi mình giải vậy!
a) Đặt \(y=x^2+4x+8\),phương trình có dạng:
\(t^2+3x\cdot t+2x^2=0\)
\(\Leftrightarrow t^2+xt+2xt+2x^2=0\)
\(\Leftrightarrow t\left(t+x\right)+2x\left(t+x\right)=0\)
\(\Leftrightarrow\left(2x+t\right)\left(t+x\right)=0\)
\(\Leftrightarrow\left(2x+x^2+4x+8\right)\left(x^2+4x+8+x\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=-2\\x=-4\end{cases}}\)vậy tập nghiệm của phương trình là:S={-2;-4}
b) nhân 2 vế của phương trình với 12 ta được:
\(\left(6x+7\right)^2\left(6x+8\right)\left(6x+6\right)=72\)
Đặt y=6x+7, ta được:\(y^2\left(y+1\right)\left(y-1\right)=72\)
giải tiếp ra ta sẽ được S={-2/3;-5/3}
c) \(\left(x-2\right)^4+\left(x-6\right)^4=82\)
S={3;5}
d)s={1}
e) S={1;-2;-1/2}
f) phương trình vô nghiệm

a) \(5x\left(3x-7\right)-15x\left(x-1\right)=3\)
\(\Rightarrow15x^2-35x-15x^2+15x=3\)
\(\Rightarrow-20x=3\)
\(\Rightarrow x=-\dfrac{3}{20}\)
b) \(\left(4x+2\right)\left(6x-3\right)-\left(8x+5\right)\left(3x-4\right)=2\)
\(\Rightarrow24x^2+12x-12x-6-24x^2-15x+24x+20=2\)
\(\Rightarrow9x+14=2\)
\(\Rightarrow9x=-12\)
\(\Rightarrow x=-\dfrac{4}{3}\)
c) \(7x^2-21x=0\)
\(\Rightarrow7x\left(x-3\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}7x=0\\x-3=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=0\\x=3\end{matrix}\right.\)
d) \(9x^2-6x+1=0\)
\(\Rightarrow\left(3x\right)^2-2.3x+1=0\)
\(\Rightarrow\left(3x-1\right)^2=0\)
\(\Rightarrow3x-1=0\)
\(\Rightarrow3x=1\)
\(\Rightarrow x=\dfrac{1}{3}\)
e) \(16x^2-49=0\)
\(\Rightarrow\left(4x\right)^2-7^2=0\)
\(\Rightarrow\left(4x-7\right)\left(4x+7\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}4x-7=0\\4x+7=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}4x=7\\4x=-7\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=\dfrac{7}{4}\\x=-\dfrac{7}{4}\end{matrix}\right.\)
f) \(5x^3-20x=0\)
\(\Rightarrow5x\left(x^2-4\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}5x=0\\x^2-4=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=5\\x^2=4\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=5\\x=2\\x=-2\end{matrix}\right.\)
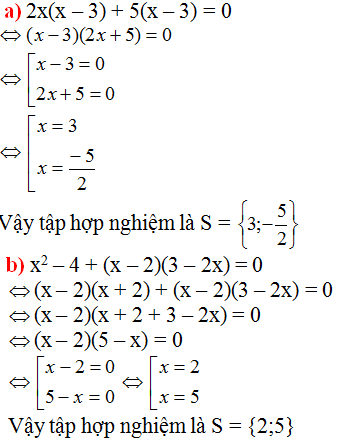
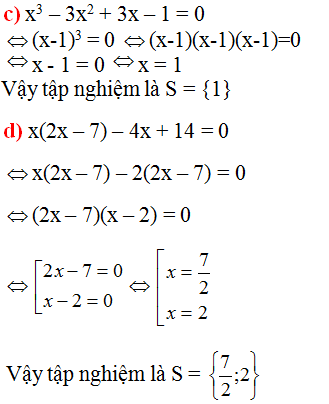
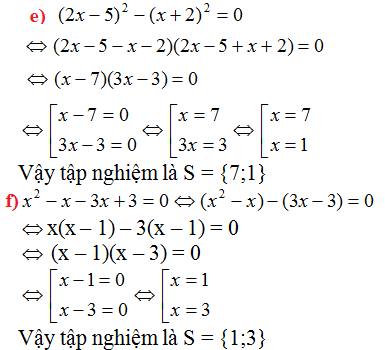
a, (3x-1)2 - (x+3)2 = 0
<=> [(3x-1)-(x+3)][(3x-1)+(x+3)] = 0
<=> (3x-1-x-3)(3x-1+x+3) = 0
<=> (2x-4)(4x+2) = 0
=> 2x-4=0 hoặc 4x+2=0
=> 2x =4 hoặc 4x = -2
=> x = 2 hoặc x = \(\frac{-1}{2}\)
\(\begin{array}{l} a){\left( {3x - 1} \right)^2} - {\left( {x + 3} \right)^2} = 0\\ \Leftrightarrow \left( {3x - 1 + x + 3} \right)\left[ {3x - 1 - x - 3} \right] = 0\\ \Leftrightarrow \left( {4x + 2} \right)\left( {2x - 4} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l} 4x + 2 = 0\\ 2x - 4 = 0 \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} x = - \dfrac{1}{2}\\ x = 2 \end{array} \right.\\ b){x^3} - \dfrac{x}{{49}} = 0\\ \Leftrightarrow 49{x^3} - x = 0\\ \Leftrightarrow x\left( {49{x^2} - 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l} x = 0\\ 49{x^2} - 1 = 0 \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} x = 0\\ x = \pm \dfrac{1}{7} \end{array} \right.\\ c){x^2} - 7x + 12 = 0\\ \Leftrightarrow {x^2} - 3x - 4x + 12 = 0\\ \Leftrightarrow x\left( {x - 3} \right) - 4\left( {x - 3} \right) = 0\\ \Leftrightarrow \left( {x - 3} \right)\left( {x - 4} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l} x - 3 = 0\\ x - 4 = 0 \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} x = 3\\ x = 4 \end{array} \right.\\ d)4{x^2} - 3x - 1 = 0\\ \Leftrightarrow 4{x^2} + x - 4x - 1 = 0\\ \Leftrightarrow x\left( {4x + 1} \right) - \left( {4x + 1} \right) = 0\\ \Leftrightarrow \left( {4x + 1} \right)\left( {x - 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l} 4x + 1 = 0\\ x - 1 = 0 \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} x = - \dfrac{1}{4}\\ x = 1 \end{array} \right.\\ e){x^3} - 2x - 4 = 0\\ \Leftrightarrow {x^3} - 4x + 2x - 4 = 0\\ \Leftrightarrow x\left( {{x^2} - 4} \right) + 2\left( {x - 2} \right) = 0\\ \Leftrightarrow x\left( {x - 2} \right)\left( {x + 2} \right) + 2\left( {x - 2} \right) = 0\\ \Leftrightarrow \left( {x - 2} \right)\left[ {x\left( {x + 2} \right) + 2} \right] = 0\\ \Leftrightarrow \left( {x - 2} \right)\left( {{x^2} + 2x + 2} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l} x - 2 = 0\\ {x^2} + 2x + 2 = 0 \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} x = 2\\ {x^2} + 2x + 2x = 0\left( {VN} \right) \end{array} \right.\\ f){x^3} + 8{x^2} + 17x + 10 = 0\\ \Leftrightarrow \left( {x + 1} \right)\left( {{x^2} + 7x + 10} \right) = 0\\ \Leftrightarrow \left( {x + 1} \right)\left( {{x^2} + 5x + 2x + 10} \right) = 0\\ \Leftrightarrow \left( {x + 1} \right)\left[ {x\left( {x + 5} \right) + 2\left( {x + 5} \right)} \right] = 0\\ \Leftrightarrow \left( {x + 1} \right)\left( {x + 5} \right)\left( {x + 2} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l} x + 1 = 0\\ x + 5 = 0\\ x + 2 = 0 \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} x = - 1\\ x = - 5\\ x = - 2 \end{array} \right. \end{array}\)