Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
a.
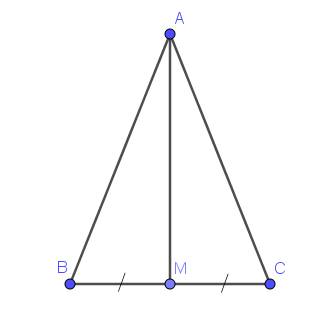
Do tam giác $ABC$ cân tại $A$ nên $AB=AC$
Xét tam giác $ABM$ và $ACM$ có:
$AB=AC$
$AM$ chung
$BM=CM$ (do $M$ là trung điểm $BC$)
$\Rightarrow \triangle ABM=\triangle ACM$ (c.c.c)
b.
Từ tam giác bằng nhau phần a suy ra $\widehat{BAM}=\widehat{CAM}$. Mà $AM$ nằm giữa $AB, AC$ nên $AM$ là tia phân giác $\widehat{BAC}$
Cũng từ tam giác bằng nhau phần a suy ra:
$\widehat{AMB}=\widehat{AMC}$
Mà $\widehat{AMB}+\widehat{AMC}=\widehat{BMC}=180^0$
$\Rightarrow \widehat{AMB}=180^0:2=90^0$
$\Rightarrow AM\perp BC$
c.
$AM\perp BC, M$ là trung điểm $BC$ nên $AM$ là đường trung trực của $BC$
$\Rightarrow$ mọi điểm $E\in AM$ đều cách đều 2 đầu mút B,C (theo tính chất đường trung trực)
$\Rightarrow EB=EC$
$\Rightarrow \triangle EBC$ cân tại $E$.

bạn tự vẽ hình
a, xét tam giác ABM và tam giác ACM có :
AB=AC (gt)
MB=MC (gt)
AM là cạch chung
suy ra tam giác ABM =tam giác ACN (c.c.c)
b, Vì tam giác ABM = tam giác ACN (câu a)
suy ra góc M1= góc M2 (2 góc tương ứng)
mà M1+M2=180 ( 2 góc kề bù)
suy ra : M1=M2= 90
suy ra AM vuông góc BC
c, Vì tam giác ABM = tam giác ACM (câu a)
suy ra : A1=A2 ( 2 góc tương ứng)
suy ra: AM là phân giác góc BAC
bn vẽ hình giùm mik nha
a) xét tam giác ABM và tam giác ACM có:
AM cạnh chung
BM=MC(M trđ BC)
AB=AC(gt)
Nên tam giác ABM = tam giác ACM(ccc)
b) Từ c/m a có: tam giác ABM=tam giác ACM => góc AMB = góc AMC mà AMB+AMC=180 độ(kề bù)
hay 2.AMB=180 độ => AMB=90 độ => AM vuông BC
c) Có tam giác ABM = tam giác ACM => BAM=CAM kết hợp AM nằm giữa AB và AC => AM p/g BAC

A B C M 1 2 Q G
A) XÉT \(\Delta ABM\)VÀ\(\Delta ACM\)CÓ
\(AB=AC\left(GT\right)\)
\(\widehat{A_1}=\widehat{A_2}\left(GT\right)\)
AM LÀ CẠNH CHUNG
=>\(\Delta ABM\)=\(\Delta ACM\)( C-G-C)
TRONG TAM GIÁC CÂN TIA PHÂN GIÁC CŨNG LÀ ĐƯỜNG CAO
=> AM LÀ ĐƯỜNG CAO CỦA \(\Delta ABC\)
\(\Rightarrow AM\perp BC\)
B) TRONG TAM GIÁC CÂN TIA PHÂN GIÁC CŨNG LÀ TRUNG TUYẾN
=> AM LÀ TRUNG TUYẾN THỨ NHẤT CỦA \(\Delta ABC\)
MÀ BG LÀ ĐƯỜNG TRUNG TUYẾN THỨ HAI CỦA \(\Delta ABC\)
HAI ĐƯỜNG TRUNG TUYẾN NÀY CẮT NHAU TẠI G
\(\Rightarrow G\)LÀ TRỌNG TÂM CỦA \(\Delta ABC\)
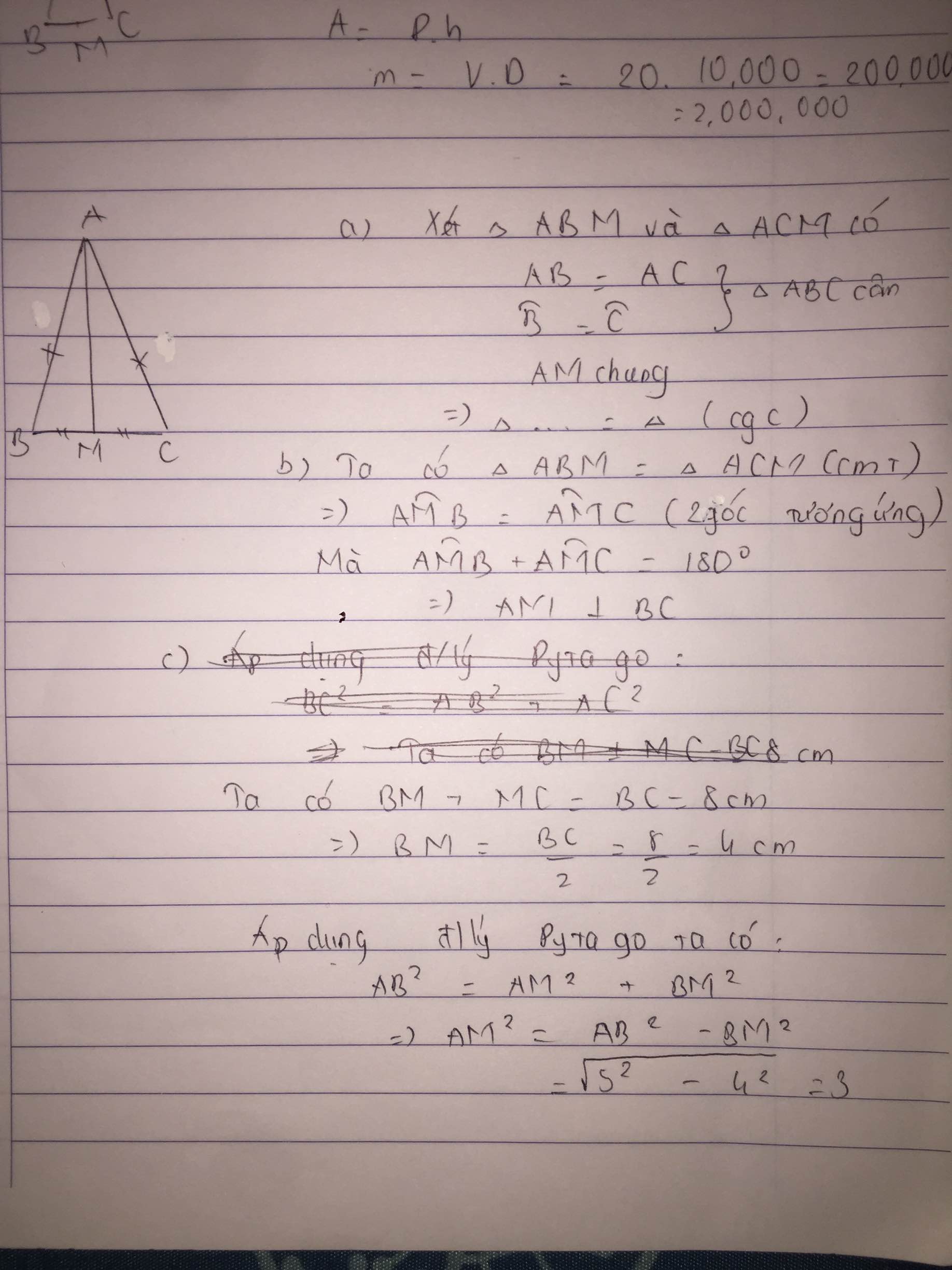



xin gửi cho ng ae https://books.google.com.vn/books?id=owlmDwAAQBAJ&pg=PA58&lpg=PA58&dq=B%C3%A0i+to%C3%A1n+2:+tam+gi%C3%A1c+ABC+c%C3%A2n+t%E1%BA%A1i+A,+g%E1%BB%8Di+M+l%C3%A0+trung+%C4%91i%E1%BB%83m+c%E1%BB%A7a+BC+1,+Ch%E1%BB%A9ng+minh+AM+vu%C3%B4ng+g%C3%B3c+v+%E1%BB%9Bi+BC+AM+l%C3%A0+ph%C3%A2n+gi%C3%A1c+G%C3%B3c+BAC+2,+cho+BC+%3D6+cm,+AB+%3D10cm.+T%C3%ADnh+chu+vi+tam+gi%C3%A1c+ABM&source=bl&ots=PtijT9btGV&sig=ACfU3U1yMN80kRhao_IWaDOriwmgMEhUjQ&hl=vi&sa=X&ved=2ahUKEwi_lcqqqOrnAhXhwzgGHeABBkgQ6AEwAHoECAgQAQ#v=onepage&q=B%C3%A0i%20to%C3%A1n%202%3A%20tam%20gi%C3%A1c%20ABC%20c%C3%A2n%20t%E1%BA%A1i%20A%2C%20g%E1%BB%8Di%20M%20l%C3%A0%20trung%20%C4%91i%E1%BB%83m%20c%E1%BB%A7a%20BC%201%2C%20Ch%E1%BB%A9ng%20minh%20AM%20vu%C3%B4ng%20g%C3%B3c%20v%20%E1%BB%9Bi%20BC%20AM%20l%C3%A0%20ph%C3%A2n%20gi%C3%A1c%20G%C3%B3c%20BAC%202%2C%20cho%20BC%20%3D6%20cm%2C%20AB%20%3D10cm.%20T%C3%ADnh%20chu%20vi%20tam%20gi%C3%A1c%20ABM&f=false tại vì ngu toán hình nên dùng mạng giải cho ! xl ng ae !
Damn it