Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Để (d1)//(d2) thì \(\left\{{}\begin{matrix}3m^2+1=4m\\m^2-9< >-m-5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3m^2-4m+1=0\\m^2+m-4< >0\end{matrix}\right.\)
=>m=1/3 hoặc m=1
b: Để hai đường cắt nhau thì 3m^2+1<>4m
=>m<>1/3 và m<>1
Khi m=2 thì (d1): \(y=8x-7\) và (d2): \(y=13x-5\)
Tọa độ giao là:
13x-5=8x-7 và y=8x-7
=>5x=-2 và y=8x-7
=>x=-2/5 và y=8x-7
=>x=-2/5 và y=-16/5-7=-51/5

a: Để d1//d2 thì \(\left\{{}\begin{matrix}3m^2+1-4m=0\\-m-5< >m^2-9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(3m-1\right)\left(m-1\right)=0\\m^2-9+m+5< >0\end{matrix}\right.\)
=>m=1/3 hoặc m=1
b: Để hai đường cắt nhau thì (3m-1)(m-1)<>0
hay \(m\notin\left\{\dfrac{1}{3};1\right\}\)

Bài 1)
a) Xét phương trình hoành độ giao điểm: \(2x+3+m=3x+5-m\)
\(\Leftrightarrow x=3+m+m-5\Leftrightarrow x=2m-2\)
Để giao điểm của hai đường thẳng trên nằm trên trục tung thì \(2m-2=0\Leftrightarrow m=1\)
b) Do (d) // (d') nên (d) có phương trình \(y=-\frac{1}{2}x+b\)
Do (d) cắt trục hoành tại điểm có hoành độ x = 10 nên điểm (10;0) thuộc đường thẳng (d0.
Vậy thì \(0=-\frac{1}{2}.10+b\Leftrightarrow b=5\)
Vậy phương trình đường thẳng (d) là \(y=-\frac{1}{2}x+5\)
Bài 2)
a) Để (d1)//(d2) thì \(4m=3m+1\Leftrightarrow m=1\)
b) Để (d1)//(d2) thì \(4m\ne3m+1\Leftrightarrow m\ne1\)
Khi m = 2, ta có phương trình hoành độ giao điểm là:
\(8x-7=7x-7\Leftrightarrow x=0\)
Với \(x=0,y=-7\)
Vậy tọa độ giao điểm của (d1) và (d2) là (0; -7)

a) Để d1 trùng d2 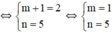
Vậy m = 1, n = 5
b) Để d1 cắt d2 thì: m + 1 ≠ 2 ⇒ m ≠ 1
c) Để d1 song song d2 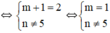
Vậy m = 1, n ≠ 5.

a) Để d1 trùng d2 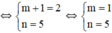
Vậy m = 1, n = 5
b) Để d1 cắt d2 thì: m + 1 ≠ 2 ⇒ m ≠ 1
c) Để d1 song song d2 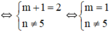
Vậy m = 1, n ≠ 5.
sos
cứu với mn