Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

I . Trắc Nghiệm
1B . 2D . 3C . 5A
II . Tự luận
2,a,Ta có: A+(x\(^2\)y-2xy\(^2\)+5xy+1)=-2x\(^2\)y+xy\(^2\)-xy-1
\(\Leftrightarrow\) A=(-2x\(^2\)y+xy\(^2\)-xy-1) - (x\(^2\)y-2xy\(^2\)+5xy+1)
=-2x\(^2\)y+xy\(^2\)-xy-1 - x\(^2\)y+2xy\(^2\)-5xy-1
=(-2x\(^2\)y - x\(^2\)y) + (xy\(^2\)+ 2xy\(^2\)) + (-xy - 5xy ) + (-1 - 1)
= -3x\(^2\)y + 3xy\(^2\) - 6xy - 2
b, thay x=1,y=2 vào đa thức A
Ta có A= -3x\(^2\)y + 3xy\(^2\) - 6xy - 2
= -3 . 1\(^2\) . 2 + 3 .1 . 2\(^2\) - 6 . 1 . 2 -2
= -6 + 12 - 12 - 2
= -8
3,Sắp xếp
f(x) =9-x\(^5\)+4x-2x\(^3\)+x\(^2\)-7x\(^4\)
=9-x\(^5\)-7x\(^4\)-2x\(^3\)+x\(^2\)+4x
g(x) = x\(^5\)-9+2x\(^2\)+7x\(^4\)+2x\(^3\)-3x
=-9+x\(^5\)+7x\(^4\)+2x\(^3\)+2x\(^2\)-3x
b,f(x) + g(x)=(9-x\(^5\)-7x\(^4\)-2x\(^3\)+x\(^2\)+4x) + (-9+x\(^5\)+7x\(^4\)+2x\(^3\)+2x\(^2\)-3x)
=9-x\(^5\)-7x\(^4\)-2x\(^3\)+x\(^2\)+4x-9+x\(^5\)+7x\(^4\)+2x\(^3\)+2x\(^2\)-3x
=(9-9)+(-x\(^5\)+x\(^5\))+(-7x\(^4\)+7x\(^4\))+(-2x\(^3\)+2x\(^3\))+(x\(^2\)+2x\(^2\))+(4x-3x)
= 3x\(^2\) + x
g(x)-f(x)=(-9+x\(^5\)+7x\(^4\)+2x\(^3\)+2x\(^2\)-3x) - (9-x\(^5\)-7x\(^4\)-2x\(^3\)+x\(^2\)+4x)
=-9+x\(^5\)+7x\(^4\)+2x\(^3\)+2x\(^2\)-3x-9+x\(^5\)+7x\(^4\)+2x \(^3\)-x\(^2\)-4x
=(-9-9)+(x\(^5\)+x\(^5\))+(7x\(^4\)+7x\(^4\))+(2x\(^3\)+2x\(^3\))+(2x\(^2\)-x\(^2\))+(3x-4x)
= -18 + 2x\(^5\) + 14x\(^4\) + 4x\(^3\) + x\(^2\) - x

a.
\(3x^2\left(2x^3-x+5\right)=6x^5-3x^3+15x^2\)
\(\Rightarrow6x^5-3x^3+15x^2=6x^5-3x^3+15x^2\)
\(=6x^5-3x^2+15x^2-6x^5-3x^3+15x^2\)
= 0
b.
\(\left(4xy+3y-5x\right)x^2y=4x^3y^2+3x^2y^2-5x^3y\)
\(\Rightarrow4x^3y^2+3x^2y^2-5x^3y=4x^3y^2+3x^2y^2-5x^3y\)
= 0

Lời giải:
Nếu $a\neq 0$ thì đa thức $M$ có bậc là $12+3=15\neq 5$ (trái với đề bài)
Nếu $a=0$ thì $M=-2xy+6x^3y^2$ có bậc $3+2=5$ (thỏa mãn)
Vậy $a=0$
---------------------
$N=-3xy^4+6x^3y^7+(a+1)x^3y^7-7xy$
$=-3xy^4+(a+7)x^3y^7-7xy$
Nếu $a+7\neq 0$ thì bậc của $N$ là $3+7=10\neq 5$ (trái đề)
Nếu $a+7=0$ thì $N=-3xy^4-7xy$ có bậc $1+4=5$ (thỏa đề)
Vậy $a+7=0\Leftrightarrow a=-7$

a)= \(4x^2y+2x^2y-5x^2y-3y^3-5y^3-6xy^2\)
=\(2x^2y-8y^3-6xy\)
b) =\(2xyz-8xyz-11xy^3+2xy^3+4xy-2xy-11\)
=\(-6xyz-9xy^3+2xy-11\)
mình ko viết đề bài đâu ![]() 2 câu còn lại làm tương tự nhé
2 câu còn lại làm tương tự nhé![]()
a. \(4x^2y-3y^3-6xy^2-5y^3+2x^2y-5x^2y\)
\(=-8y^3+x^2y-6xy^2\)
b. \(2xyz-11xy^3-8xyz+2xy^3+4xy-11-2xy\)
\(=-6xyz-9xy^3+2xy-11\)
c. \(x\left(x-5\right)-3x\left(x-1\right)+6\left(x-2\right)\)
\(=x^2-5x-3x^2-3x+6x-12\)
\(=-2x^2-2x-12\)
d. \(x^3\left(x-2\right)-2x^2\left(x^2-x\right)+5\left(2x^4-1\right)\)
\(=x^4-2x^3-2x^4-2x^3+10x^4-5\)
\(=9x^4-4x^3-5\)

Bài 5:
a)
\(F=3x^3y+6x^2y^2+3xy^3=3xy(x^2+2xy+y^2)=3xy(x+y)^2\)
\(=3.\frac{1}{2}.\frac{-1}{3}(\frac{1}{2}+\frac{-1}{3})^2=\frac{-1}{72}\)
b)
\(G=x^2y^2+xy+x^3+y^3=(-1)^2(-3)^2+(-1)(-3)+(-1)^3+(-3)^3\)
\(=9+3-1-27=-18\)
Bài 7:
a)
\(x^2+2x=0\Leftrightarrow x(x+2)=0\Rightarrow \left[\begin{matrix} x=0\\ x+2=0\end{matrix}\right. \Rightarrow \left[\begin{matrix} x=0\\ x=-2\end{matrix}\right.\)
Vậy đa thức có nghiệm $x=0; x=-2$
b)
\(-5x^4=0\Leftrightarrow x^4=0\Leftrightarrow x=0\)
Vậy đa thức có nghiệm $x=0$
c)
\(x^2+\sqrt{5}=0\Leftrightarrow x^2=-\sqrt{5}< 0\) (vô lý do bình phương một số thực luôn không âm)
Do đó đa thức vô nghiệm.
d)
\((x^2+3)(-6-4x^4)=0\Rightarrow \left[\begin{matrix} x^2+3=0\\ -6-4x^4=0\end{matrix}\right.\Rightarrow \left[\begin{matrix} x^2=-3< 0\\ x^4=\frac{-3}{2}< 0\end{matrix}\right.\) (vô lý)
Do đó đa thức vô nghiệm.
e)
\(3x^8+6=0\Leftrightarrow 3(x^4)^2=-6< 0\) (vô lý)
Do đó đa thức vô nghiệm.
f)
\(x^2+2x-3=0\Leftrightarrow x^2-x+3x-3=0\Leftrightarrow x(x-1)+3(x-1)=0\)
\(\Leftrightarrow (x-1)(x+3)=0\Rightarrow \left[\begin{matrix} x=1\\ x=-3\end{matrix}\right.\)
Đa thức có nghiệm $x=1, x=-3$
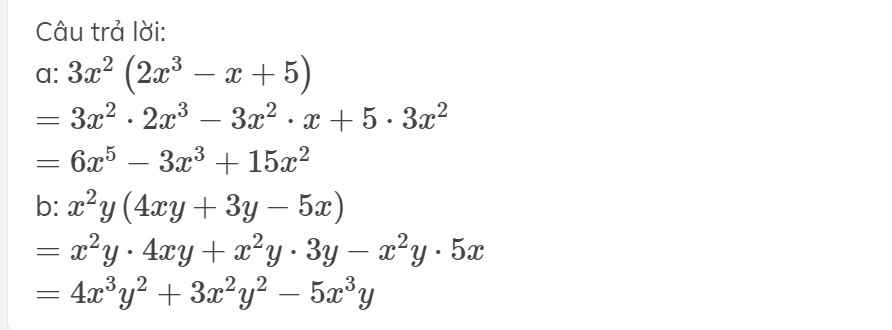
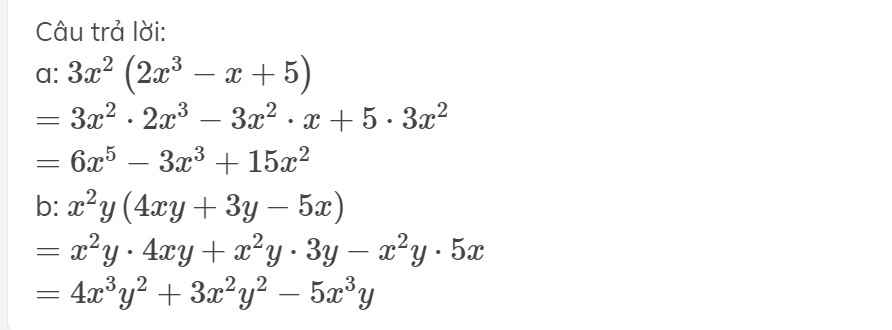
hangbich ơi chị nhớ em không????
luonghong567 ở trong hoidap247.com ý