
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


.
Tứ giác EFGH là hình bình hành.
Cách 1: EB = EA, FB = FC (gt)
nên EF là đường trung bình của ∆ABC.
Do đó EF // AC
Tương tự HG là đường trung bình của ∆ACD.
Do đó HG // AC
Suy ra EF // HG (1)
Tương tự EH // FG (2)
Từ (1) và (2) suy ra EFGH là hình bình hành (dấu hiêu nhận biết 1).
Cách 2: EF là đường trung bình của ∆ABC nên EF = AC.
HG là đường trung bình của ∆ACD nên HG = AC.
Suy ra EF = HG
Lại có EF // HG ( chứng minh trên)
Vậy EFGH là hình bình hành (dấu hiệu nhận biết 3)

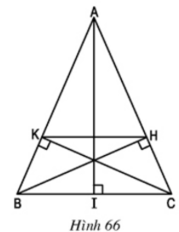
A B C K H I
a) Xét hai Δvuông HBC và ΔKCB
∠BCH = ∠CBK (Δ ABC cân tại A) BC cạnh chung
⇒ ΔHBC = ΔKCB (cạnh huyền, góc nhọn)
⇒ CH = BK
b) Ta có: AB = AC (ΔABC cân tại A) và CH = BK
- Quảng cáo -
AK = AB – BK và AH = AC – CH ⇒ AK = AH
⇒ AK/AB = AH/AC ⇒ KH//BC
c) Kẻ đường cao AI của Δ ABC và xét Δ IAC
ΔHBC có ∠ACI = ∠BCH
⇒ ΔIAC ∽ ΔHBC(g.g) ⇒ AC/BC = IC/HC ⇒ HC = IC.BC / AC = a2/2b
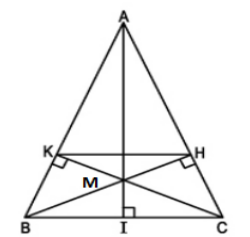
Ta có : \(KH//BC\Rightarrow\frac{KH}{BC}=\frac{AH}{AC}\)
\(\Rightarrow KH=\frac{AH.BC}{AC}=\frac{\left(AC-HC\right).BC}{AC}\)
\(\Rightarrow KH=\left(b-\frac{a^2}{2b}\right)\frac{a}{b}=a-\frac{a^3}{2b^2}\)

a)\(\frac{3xy}{9y}=\frac{\left(3y\right)x}{3.\left(3y\right)}=\frac{x}{3}\)(đúng)
b)\(\frac{3xy+3}{9y+3}=\frac{3\left(xy+1\right)}{3\left(3y+1\right)}=\frac{xy+1}{3y+1}\ne\frac{x}{3}\)(sai)
c)\(\frac{3xy+3}{9y+9}=\frac{3\left(xy+1\right)}{9\left(y+1\right)}=\frac{xy+1}{3\left(y+1\right)}\ne\frac{x+1}{3+3}=\frac{x+1}{6}\)(sai)
d)\(\frac{3xy+3x}{9y+9}=\frac{3y\left(y+1\right)}{9\left(y+1\right)}=\frac{x}{3}\)(đúng)

Để xét xem tứ giác nào là hình thang cân ta dùng tính chất
"Trong hình thang cân hai cạnh bên bằng nhau"
Tứ giác ABCD là hình thang cân vì có AD = BC.
Tứ giác EFGH không là hình thang cân vì EF > GH.
Bạn nào giúp mình giải bài toán hình 8 này với: bài 26 sgk đổi 16 là y còn y là 16. MÌNH TẶNG 5 LIKE





==" có ai ranh ko mở sách giúp bn này ik
sao thánh ko giải luôn đi