Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Với giả thiết ở đề bài, ta có thể tính được r từ đó tính được diện tích mặt cầu gần bằng \(26cm^2\)
b) Tương tự câu a, ta tính được thể tích hình nón là \(7,9cm^3\)
Thể tích của hình trụ là: π m 2 k
Thể tích của hình nón là: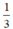 
π
m
2
k
Vậy thể tích của hình nón bằng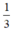 
thể tích hình trụ. Do đó, khi chứa đầy cát vào hình nón rồi đổ hết sang hình trụ thì độ cao của cát trong hình trụ sẽ là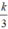 
Giải:
a) Ta có: C = 13m, h = 3cm
Diện tích xung quanh của hình trụ là: Sxp = 2 πr.h = C.h = 13.3 = 39 cm2
b) Ta có r = 5 mm , h = 8mm
Thể tích của hình trụ là:
V = πr2h = π.52.8 = 200π ≈ 628 mm3
a) Giá trị gần đúng của h là : 10,5 cm
b) Giá trị của r là : 24 cm
a) Diện tích xung quanh của hình trụ là :
Sxq = 2πr.h = 2.3,142.6,9 ≈ 339 (cm2)
b) Thể tích hình trụ là :
V = πR2.h = 3,142.62.9 ≈ 1018 (cm3)
a) Diện tích xung quanh của hình trụ là :
Sxq = 2πr.h = 2.3,142.6,9 ≈ 339 (cm2)
b) Thể tích hình trụ là : V = πR2.h = 3,142.62.9 ≈ 1018 (cm
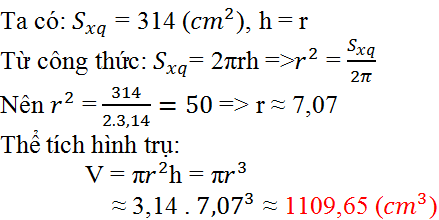
V trụ=15*3^2*pi=135pi
V nón=1/3*pi*3^2*8=24pi
=>V=159pi
V trụ=15*3^2*pi=135pi
V nón=1/3*pi*3^2*8=24pi
=>V=159pi