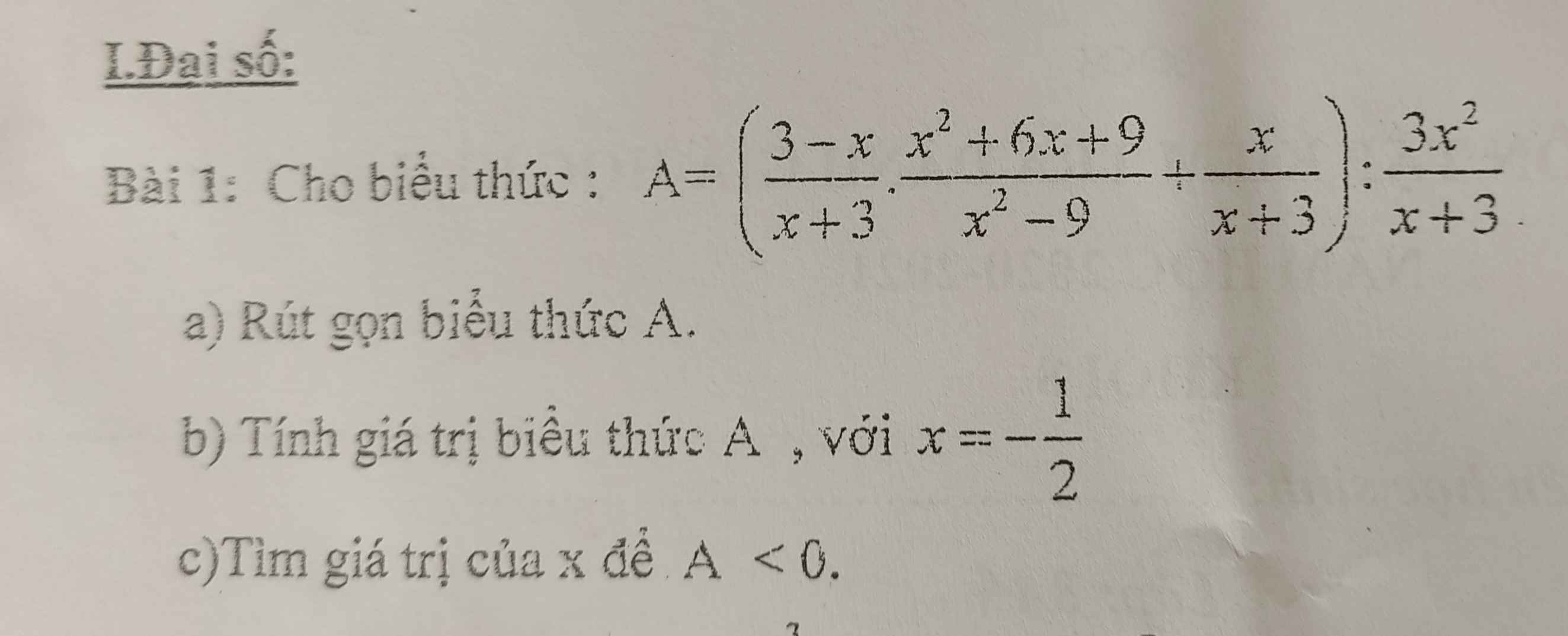K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
28 tháng 12 2021
Bài 4:
a: Xét tứ giác ANBH có
M là trung điểm của AB
M là trung điểm của NH
Do đó: ANBH là hình bình hành
mà \(\widehat{AHB}=90^0\)
nên ANBH là hình chữ nhật
17 tháng 4 2022
Bài V:
-ĐKXĐ: \(x\ne\pm1\).
\(\dfrac{m}{x-1}+\dfrac{x}{x+1}=\dfrac{x^2}{x^2-1}\)
\(\Leftrightarrow\dfrac{m\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}+\dfrac{x\left(x-1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{x^2}{\left(x-1\right)\left(x+1\right)}\)
\(\Rightarrow mx+m+x^2-x=x^2\)
\(\Leftrightarrow m\left(x+1\right)=x\)
\(\Leftrightarrow m=\dfrac{x}{x+1}\)
-Vì m,x nguyên:
\(\Rightarrow x⋮\left(x+1\right)\)
\(\Rightarrow\left(x+1-1\right)⋮\left(x+1\right)\)
\(\Rightarrow-1⋮\left(x+1\right)\)
\(\Rightarrow\left(x+1\right)\in\left\{1;-1\right\}\)
\(\Rightarrow x\in\left\{0;-2\right\}\) (nhận)
*\(x=0\Rightarrow m=\dfrac{x}{x+1}=\dfrac{0}{0+1}=0\)
\(x=-2\Rightarrow m=\dfrac{x}{x+1}=\dfrac{-2}{-2+1}=1\)
-Vậy với \(m=0\) thì \(S=\left\{0\right\}\)
với \(m=1\) thì \(S=\left\{-2\right\}\)
17 tháng 4 2022
\(\left|2x-3\right|=3-2x\)
\(ĐK:x\le\dfrac{3}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=3-2x\\3-2x=3-2x\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\0=0\left(đúng\right)\end{matrix}\right.\)
Vậy \(S=\left\{x\in R;x=\dfrac{3}{2}\right\}\)
LM
ai giải giúp em mấy bài toán này vs ạ giải chi tiết giúp em ạ
2
10 tháng 11 2021
\(1,\\ a,=6x^4y^4-x^3y^3+\dfrac{1}{2}x^4y^2\\ b,=4x^3+5x^2-8x^2-10x+12x+15\\ =4x^3-3x^2+2x+15\\ 2,\\ a,=7\left(x^2-6x+9\right)=7\left(x-3\right)^2\\ b,=\left(x-y\right)^2-36=\left(x-y-6\right)\left(x-y+6\right)\\ 3,\\ \Leftrightarrow x\left(x^2-0,36\right)=0\\ \Leftrightarrow x\left(x-0,6\right)\left(x+0,6\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=0,6\\x=-0,6\end{matrix}\right.\)
AH
Akai Haruma
Giáo viên
12 tháng 7 2021
Lời giải:
ĐKXĐ: $x\neq \pm 3; x\neq 0$
a. \(A=\left[\frac{-(x-3)}{x+3}.\frac{(x+3)^2}{(x-3)(x+3)}+\frac{x}{x+3}\right].\frac{x+3}{3x^2}\)
\(=\left(-1+\frac{x}{x+3}\right).\frac{x+3}{3x^2}=\frac{-3}{x+3}.\frac{x+3}{3x^2}=\frac{-1}{x^2}\)
b. Với $x=\frac{-1}{2}$ thì $x^2=\frac{1}{4}$
$\Rightarrow A=\frac{-1}{\frac{1}{4}}=-4$
c.
Với $x\neq 0, \pm 3$ thì $\frac{1}{x^2}>0\Leftrightarrow A=\frac{-1}{x^2}< 0$ với mọi $x\neq 0; x\neq \pm 3$
12 tháng 7 2021
a) Ta có: \(A=\left(\dfrac{3-x}{x+3}\cdot\dfrac{x^2+6x+9}{x^2-9}+\dfrac{x}{x+3}\right):\dfrac{3x^2}{x+3}\)
\(=\left(\dfrac{-\left(x-3\right)}{x+3}\cdot\dfrac{\left(x+3\right)^2}{\left(x+3\right)\left(x-3\right)}+\dfrac{x}{x+3}\right):\dfrac{3x^2}{x+3}\)
\(=\left(\dfrac{-x-3+x}{x+3}\right)\cdot\dfrac{x+3}{3x^2}\)
\(=-\dfrac{1}{x^2}\)
25 tháng 10 2021
Bài 4:
a: Ta có: \(\widehat{OAB}=\widehat{ODC}\)
\(\widehat{OBA}=\widehat{OCD}\)
mà \(\widehat{ODC}=\widehat{OCD}\)
nên \(\widehat{OAB}=\widehat{OBA}\)
hay ΔOAB cân tại O
DM
2
MH
17 tháng 9 2021
b)\(3x\left(x+3y\right)-6xy\left(x+3y\right)\)
\(=\left(3x-6xy\right)\left(x+3y\right)\)
c)\(x\left(x+y\right)-5x-5y\)
\(=x\left(x+y\right)-5\left(x+y\right)\)
\(=\left(x-5\right)\left(x+y\right)\)
HP
17 tháng 9 2021
Bài 1:
b. \(3x\left(x+3y\right)-6xy\left(x+3y\right)\)
= (3x - 6xy)(x + 3y)
= 3x(1 - 2y)(x + 3y)
c. \(x\left(x+y\right)-5x-5y\)
= x(x + y) - 5(x + y)
= (x - 5)(x + y)
d. \(3\left(x-y\right)-5x\left(y-x\right)\)
= 3(x - y) + 5x(x - y)
= (3 + 5x)(x - y)
Bài 3:
a. x + 6x2 = 0
<=> x(1 + 6x) = 0
<=> \(\left[{}\begin{matrix}x=0\\1+6x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{-1}{6}\end{matrix}\right.\)
b. 2(x + 3) - x(x + 3) = 0
<=> (2 - x)(x + 3) = 0
<=> \(\left[{}\begin{matrix}2-x=0\\x+3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-3\end{matrix}\right.\)
c. 5x(x - 2) - (2 - x) = 0
<=> 5x(x - 2) + (x - 2) = 0
<=> (5x + 1)(x - 2) = 0
<=> \(\left[{}\begin{matrix}5x+1=0\\x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-1}{5}\\x=2\end{matrix}\right.\)
d. (x + 1) = (x + 1)2
<=> (x + 1) - (x + 1)2 = 0
<=> (1 - x - 1)(x + 1) = 0
<=> -x(x + 1) = 0
<=> \(\left[{}\begin{matrix}-x=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-1\end{matrix}\right.\)
9 tháng 1 2022
Bài 2:
a: Xét ΔABC có
X là trung điểm của BC
Y là trung điểm của AB
Do đó: XY là đường trung bình
=>XY//AC và XY=AC/2=3,5(cm)
hay XZ//AC và XZ=AC
b: Xét tứ giác AZBX có
Y là trung điểm của AB
Y là trung điểm của ZX
Do đó: AZBX là hình bình hành
mà \(\widehat{AXB}=90^0\)
nên AZBX là hình chữ nhật
d: Xét tứ giác AZXC có
XZ//AC
XZ=AC
Do đó: AZXC là hình bình hành