Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
3.
a) thay vào hàm số y=f(x)=-2x+3, ta đc:
f(-2)=-2.(-2)+3=7
f(-1)=-2.(-1)+3=5
f(0)=-2.0+3=3
\(f\left(-\frac{1}{2}\right)=-2.\left(-\frac{1}{2}\right)+3=4\)
\(f\left(\frac{1}{2}\right)=-2.\frac{1}{2}+3=2\)
+)Thay xA=\(\dfrac{-1}{3}\) vào hàm số y=3x-1:
y=\(3.\dfrac{-1}{3}-1=-1-1=-2\ne y_A\)
A ko thuộc đồ thị hàm số y=3x-1.
+)Thay xB=\(\dfrac{1}{3}\)vào hàm số y=3x-1:
y=\(\dfrac{1}{3}.3-1=1-1=0=y_B\)
B thuộc đồ thi hàm số y=3x-1.
+)Thay xC=0 vào hàm số y=3x-1:
y=\(0.\dfrac{1}{3}-1=0-1=-1\ne y_C\)
C ko thuộc đồ thị hàm số y=3x-1.
+)Thay xD=0 vào hàm số y=3x-1:
y=\(0.\dfrac{1}{3}-1=0-1=-1=y_D\)
D thuộc đồ thị hàm số y=3x-1.
Vậy điểm B,D ko thuộc đồ thị hàm số y=3x-1.
Ta có: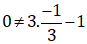 
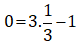
nên điểm A không thuộc đồ thị hàm số y = 3x-1
nên điểm B thuộc đồ thị hàm số y=3x-1.
1 ≠ 3.0 – 1 nên điểm C không thuộc đồ thị hàm số y = 3x – 1.
-1 = 3.0 – 1 nên điểm D thuộc đồ thị hàm số y = 3x – 1.
\(\frac{4}{5}x+0=4,5\)
\(\frac{4}{5}x=4,5\)
\(x=4,5:\frac{4}{5}\)
\(x=5,625\)
vậy \(x=5,625\)
\(\frac{x}{3}=\frac{-5}{9}\)
\(\Rightarrow9x=-5.3\)
\(\Rightarrow9x=-15\)
\(\Rightarrow x=\frac{-5}{3}\)
vậy \(x=\frac{-5}{3}\)
\(\left|x+5\right|-\frac{1}{3}=\frac{2}{3}\)
\(\left|x+5\right|=\frac{2}{3}+\frac{1}{3}\)
\(\left|x+5\right|=1\)
\(\Rightarrow\orbr{\begin{cases}x+5=1\\x+5=-1\end{cases}}\Rightarrow\orbr{\begin{cases}x=-4\\x=-6\end{cases}}\)
vậy \(\orbr{\begin{cases}x=-4\\x=-6\end{cases}}\)
\(\left(x-2\right)^3=-125\)
\(\left(x-2\right)^3=\left(-5\right)^3\)
\(\Rightarrow x-2=-5\)
\(\Rightarrow x=-3\)
vậy \(x=-3\)
a/ \(x^2+y^2=0\Rightarrow\left\{{}\begin{matrix}x=0\\y=0\end{matrix}\right.\) \(\Rightarrow A=0\)
b/ Do \(x=19\Rightarrow20=x+1\)
\(B=x^6-\left(x+1\right)x^5+\left(x+1\right)x^4-\left(x+1\right)x^3+\left(x+1\right)x^2-\left(x+1\right)x+20\)
\(B=x^6-x^6-x^5+x^5+x^4-x^4-x^3+x^3+x^2-x^2-x+20\)
\(B=20-x=20-19=1\)
c/ \(x+y+z=0\Rightarrow\left\{{}\begin{matrix}x+y=-z\\x+z=-y\\y+z=-x\end{matrix}\right.\)
\(C=\frac{\left(x+y\right)}{y}.\frac{\left(y+z\right)}{z}.\frac{\left(x+z\right)}{x}=\frac{-z}{y}.\frac{-x}{z}.\frac{-y}{x}=\frac{-xyz}{xyz}=-1\)