Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a ) Xét \(\Delta ABC\)và \(\Delta EBD\) ta có :
\(\widehat{BAD}\)\(=\) \(\widehat{BED}\)( \(BD\) là phân giác \(\widehat{ABC}\))
\(BD\) là cạnh chung .
\(\widehat{ABD}\)\(=\) \(\widehat{EBD}\) \(\left(=90^o\right)\)
\(\Rightarrow\Delta ABC=\Delta EBD\) ( g.c.g ) \(\Rightarrow AD=ED\) và \(AB=EB\)( 1 )
b )
\(\left(1\right)\)\(\Rightarrow AD=DE\)
Xét \(\Delta HAD\)và \(\Delta EDC\)có:
\(\widehat{HAD}\)\(=\) \(\widehat{CED}\)\(=\) \(90^o\)
\(AD=DE\)
\(\widehat{ADH}\)\(=\) \(\widehat{EDC}\) ( đối đỉnh )
\(\Rightarrow\Delta ADH=\Delta EDC\) ( g.c.g ) ( 2 )
c,
\(\left(2\right)\)\(\Rightarrow AH=EC\)
Xét \(\Delta AHC\)và \(\Delta ECH\) có:
\(\widehat{HAC}\)\(=\) \(\widehat{CEH}\)\(=90^o\)
\(HC\) là cạnh chung .
\(HA=CE\)
\(\Rightarrow\Delta HAC=\Delta CEH\) ( ch .cgv )
d,
\(\left(1\right)\)\(\Rightarrow AB=BE\)
Xét \(\Delta BEH\) và \(\Delta BAC\) có:
\(\widehat{BEH}\)\(=\) \(\widehat{BAC}\)\(=90^o\)
\(BE=AB\)
\(\widehat{HBC}\) chung .
\(\Rightarrow\Delta BEH=\Delta BAC\) ( g.c.g )

tự kẻ hình
a, xét tam giác ABD và tam giác EBD có : BD chung
gcs DEB = góc DAB = 90 do ...
góc ABD = góc EBD do BD là phân giác của góc ABC (gt)
=> tam giác ABD = tam giác EBD (ch-gn)
b, tam giác ABD = tam giác EBD (câu a)
=> AD = DE (Đn)
xét tam giác ADH và tam giác EDC có : góc CDE = góc HDA (Đối đỉnh)
góc CED = góc DAH = 90
=> tam giác ADH = tam giác EDC (cgv-gnk)
a, xét tam giác ABD và tam giác EBD có : BD chung
gcs DEB = góc DAB = 90 do ...
góc ABD = góc EBD do BD là phân giác của góc ABC (gt)
=> tam giác ABD = tam giác EBD (ch-gn)
b, tam giác ABD = tam giác EBD (câu a)
=> AD = DE (Đn)
xét tam giác ADH và tam giác EDC có : góc CDE = góc HDA (Đối đỉnh)
góc CED = góc DAH = 90
=> tam giác ADH = tam giác EDC (cgv-gnk)

a: Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔABD=ΔEBD
b: Xét ΔADH vuông tại A và ΔEDC vuông tại E có
DA=DE
\(\widehat{ADH}=\widehat{EDC}\)
Do đó: ΔADH=ΔEDC
c: Xét ΔAHC vuông tại A và ΔECH vuông tại E có
HC chung
AH=EC
Do đó: ΔAHC=ΔECH
d: Xét ΔBEH vuông tại E và ΔBAC vuông tại A có
BE=BA
BH=BC
Do đó: ΔBEH=ΔBAC
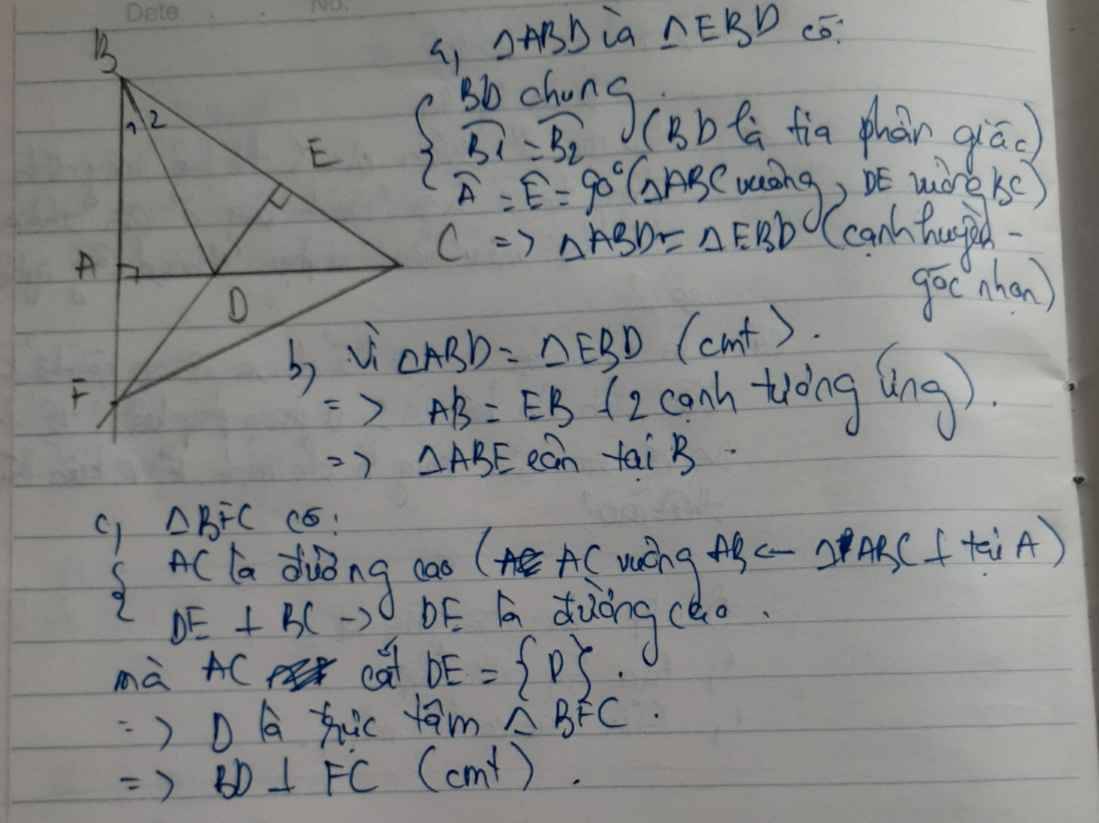
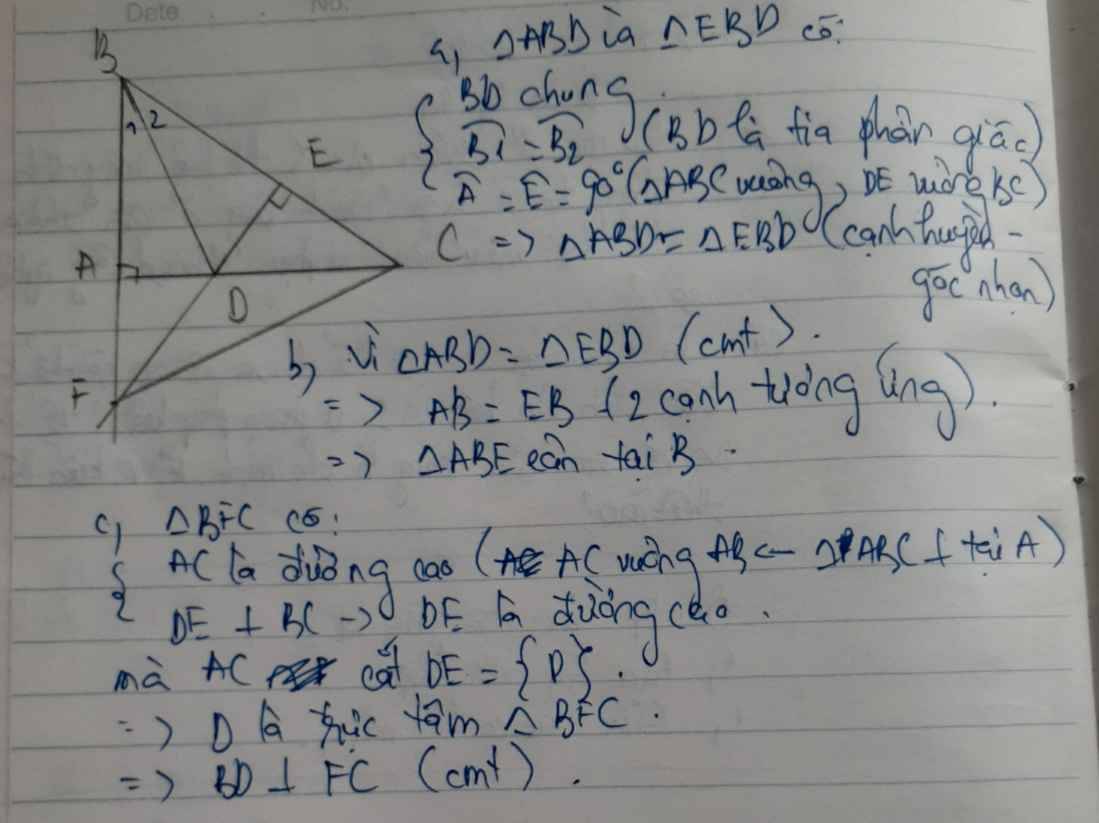
a: Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔABD=ΔEBD
b: Xét ΔADH vuông tại A và ΔEDC vuông tại E có
DA=DE
\(\widehat{ADH}=\widehat{EDC}\)
Do đó: ΔADH=ΔEDC
c: Xét ΔAHC vuông tại A và ΔECH vuông tại E có
CH chung
AH=EC
Do đó: ΔAHC=ΔECH
Cho mình xin ảnh hình ạ