Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tam giác ABC có MN//BC nên \(\frac{AM}{AB}=\frac{AN}{AC}=\frac{MN}{BC}\)(định lý Thales)
\(\frac{AM}{AB}=\frac{AN}{AC}\Rightarrow\frac{5}{15}=\frac{AN}{12}\Rightarrow AN=\frac{5.12}{15}=4\)
\(\frac{AM}{AB}=\frac{MN}{BC}\Rightarrow\frac{5}{15}=\frac{MN}{20}\Rightarrow MN=\frac{5.20}{15}=\frac{20}{3}\)
Dễ thấy MNPB là hình bình hành nên \(MN=BP=\frac{20}{3}\)
Vậy \(AN=4\);\(MN=BP=\frac{20}{3}\)

a,Do MN//Bc suy ra AM/AB = Mn/Bc (theo định lí ta let)
hay 3/12 = MN/16
suy ra: MN=4 cm.
còn 2 câu nữa bây giờ mk phải đi hk,tẹo tối về mk giải tiếp :)

tham khảo :
https://lazi.vn/edu/exercise/582904/cho-hinh-thang-abcd-ab-cd-cheo-cat-nhau-tai-o-p

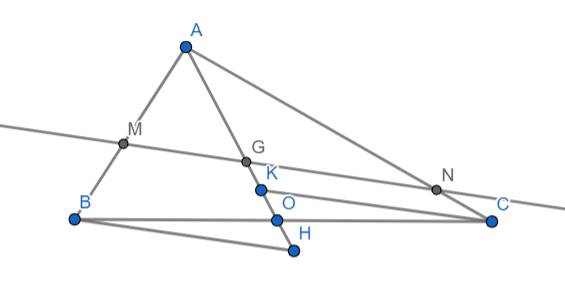
Xét 2 tam giác AMG và ABH ta có:
\(\widehat{BAH}\) chung
\(\widehat{AMG}=\widehat{ABH}\) (cặp góc đồng vị do BH//MG)
\(\Rightarrow\Delta AMG\sim\Delta ABH\left(g.g\right)\)
\(\Rightarrow\dfrac{AB}{AM}=\dfrac{AH}{AG}\) (1)
Xét 2 tam giác ANG và ACK có:
\(\widehat{CAK}\) chung
\(\widehat{ANG}=\widehat{ACK}\) (cặp góc đồng vị do CK//GN)
\(\Rightarrow\Delta ANG\sim\Delta ACK\left(g.g\right)\)
\(\Rightarrow\dfrac{AC}{AN}=\dfrac{AK}{AG}\) (2)
Xét hai tam giác BOH và COK ta có:
\(\widehat{BOH}=\widehat{COK}\) (đối đỉnh)
\(BO=CO\) (AO là đường trung tuyến nên O là trung điểm của BC)
\(\widehat{HBO}=\widehat{KCO}\) (so le trong vì BH//MN và CK//MN ⇒ BH//CK)
\(\Rightarrow\Delta BOH=\Delta COK\left(g.c.g\right)\)
\(\Rightarrow HO=OK\) (hai cạnh t.ứng)
\(\Rightarrow HK=2HO\)
Ta lấy (1) + (2) \(\Rightarrow\dfrac{AB}{AM}+\dfrac{AC}{AN}=\dfrac{AH+AK}{AG}=\dfrac{AH+AH+HK}{AG}=\dfrac{2AH+HK}{AG}\)
\(=\dfrac{2AH+2HO}{AG}=\dfrac{2\left(AH+HO\right)}{AG}=\dfrac{2AO}{AG}\)
Mà G là trọng tâm của tam giác ABC \(\Rightarrow AO=\dfrac{3}{2}AG\)
\(\Rightarrow\dfrac{AB}{AM}+\dfrac{AC}{AN}=\dfrac{2\cdot\dfrac{3}{2}AG}{AG}=2\cdot\dfrac{3}{2}=3\left(đpcm\right)\)
MN//BC nên \(\frac{MN}{BC}=\frac{AM}{AB}\Rightarrow MN=\frac{5}{15}.20=\frac{20}{3}\)
MN//BC nên \(\frac{MN}{BC}=\frac{AN}{AC}\Rightarrow AN=\frac{\frac{20}{3}}{20}.12=4\)
NP//AB nên \(\frac{AN}{AC}=\frac{BP}{BC}\Rightarrow BP=\) thế số vào
MN//CD nên \(\frac{AM}{AD}=\frac{BN}{BC}\).Lại có \(\frac{Am}{AD}=\frac{OM}{CD}\left(1\right),\frac{BN}{BC}=\frac{ON}{CD}\left(2\right)\)
nên (1)=(2) \(\frac{OM}{CD}=\frac{ON}{CD}\RightarrowĐPCM\)