Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Thể tích là:
\(\frac{3x4}{2}\)x 9 = 54 cm3
Trong tam giác vuông ABC (vuông tại A), theo định lý Pytago, ta có cạnh huyền bằng:
\(\sqrt{3^2+4^2}\) = 5 cm
Diện tích xung quanh là:
(3 + 4 + 5) x 9 = 108 cm2
Diện tích toàn phần là:
108 + 3 x 4 = 120 cm2
b. Diện tích xung quanh là:
(3 + 4) x 2 x 5 = 70 cm2
Đáp số : 70 cm2

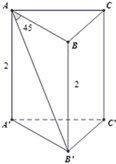
Tam giác vuông ABB' có B A B ' ^ = 45 0 nên là tam giác vuông cân tại B nên AB = BB' = 2cm.
Vì ABC là tam giác đều nên chu vi đáy bằng 6( cm )
Khi đó diện tích xung quanh hình lăng trụ là S x q = 6 . 2 = 12 ( c m 2 )
Chọn đáp án C.

a) Trong ΔΔABC vuông tại A theo định lí Pitago ta có ;
CB=√32+42=5(cm)CB=32+42=5(cm)
Diện tích xung quanh của lăng trụ :
(3 + 4 + 5).6 = 72(cm2)
b) Diện tích mặt đáy là :
12⋅3⋅4=6(cm2)12⋅3⋅4=6(cm2)
Thể tích của lăng trụ là:
6 x 6 = 36(cm2)

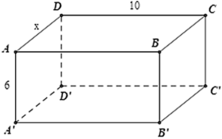
Chu vi của đáy bằng: 2( x + 10 )
Diện tích xung quanh: Sxq = 2( x + 10 ).6 = 12( x + 10 )
Diện tích đáy: 10x
Theo giả thiết ta có: 12( x + 10 ) = 20x ⇔ x = 15
Chọn đáp án A.


Câu 2:
Gọi a;b là 2 kích thước còn lại của hình hộp chữ nhật. Theo đề bài ta có:
2(a+b).h = 120
<=> 2.(a+b).6=120
<=> a+b= 10 (cm)
V lớn nhất <=> a.b.h lớn nhất<=> a.b lớn nhất mà ab < hoặc = (a+b)^2/4
Nên V lớn nhất khi a=b= 10/2=5 (cm)
Vậy V đạt giá trị lớn nhất là 5.5.6= 150 cm3 khi các kích thước của đáy bằng 5 cm
Câu 2: giải
Gọi a, b là kích thước của đáy
Tcó V=6ab nên V lớn nhất \(\Leftrightarrow\)ab lớn nhất
\(S_{xq}=120\)nên 2(a+b).6=120 hay a+b=10
Tcó ab=a(10-a)= \(-a^2+10a=-\left(a-5\right)^2+25\le25\)
Sra V=6ab\(\le\)6.25=150
Vậy thể tích lớn nhất =150\(cm^3\) khi a=b=5, tức là các cạnh đáy =5cm
CHÚC BẠN HỌC TỐT, good luck:)