Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi số cây trồng được của lớp 7A,7B,7C là a,b,c(cây)(a,b,c∈N*)
Áp dụng t/c dtsbn:
\(\dfrac{a}{4}=\dfrac{b}{6}=\dfrac{c}{3}=\dfrac{a+c-b}{4+3-6}=\dfrac{12}{1}=12\)
\(\Rightarrow\left\{{}\begin{matrix}a=12.4=48\\b=12.6=72\\c=12.3=36\end{matrix}\right.\)
Vậy....

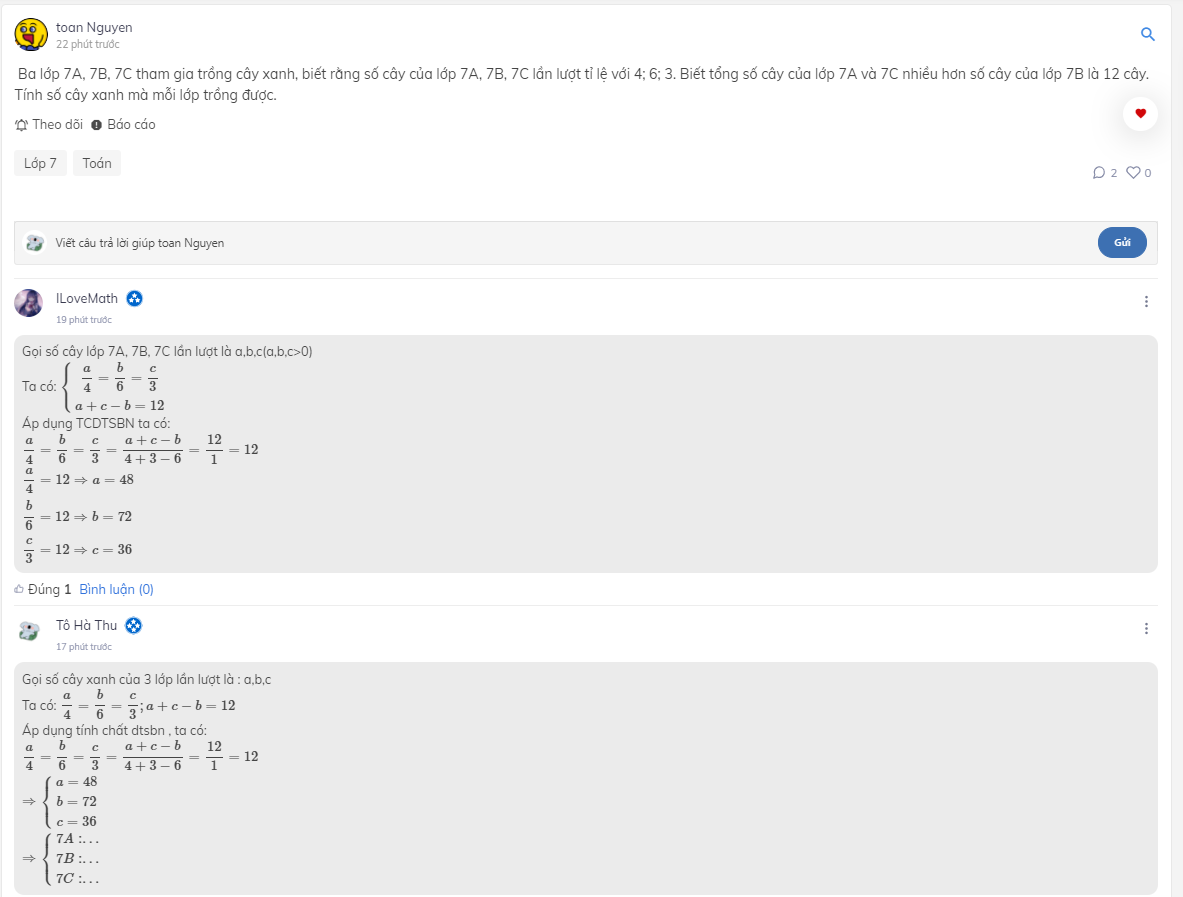
Gọi số cây lớp 7A, 7B, 7C lần lượt là a,b,c(a,b,c>0)
Ta có: \(\left\{{}\begin{matrix}\dfrac{a}{4}=\dfrac{b}{6}=\dfrac{c}{3}\\a+c-b=12\end{matrix}\right.\)
Áp dụng TCDTSBN ta có:
\(\dfrac{a}{4}=\dfrac{b}{6}=\dfrac{c}{3}=\dfrac{a+c-b}{4+3-6}=\dfrac{12}{1}=12\)
\(\dfrac{a}{4}=12\Rightarrow a=48\\ \dfrac{b}{6}=12\Rightarrow b=72\\ \dfrac{c}{3}=12\Rightarrow c=36\)
Gọi số cây xanh của 3 lớp lần lượt là : a,b,c
Ta có: \(\dfrac{a}{4}=\dfrac{b}{6}=\dfrac{c}{3};a+c-b=12\)
Áp dụng tính chất dtsbn , ta có:
\(\dfrac{a}{4}=\dfrac{b}{6}=\dfrac{c}{3}=\dfrac{a+c-b}{4+3-6}=\dfrac{12}{1}=12\)
\(\Rightarrow\left\{{}\begin{matrix}a=48\\b=72\\c=36\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}7A:...\\7B:...\\7C:...\end{matrix}\right.\)

Gọi số cây lớp 7A,7B,7C ll là a,b,c(cây;a,b,c>0)
Áp dụng t.c dtsbn:
\(\dfrac{a}{4}=\dfrac{b}{6}=\dfrac{c}{3}=\dfrac{a-b+c}{4-6+3}=\dfrac{12}{1}=12\\ \Leftrightarrow\left\{{}\begin{matrix}a=48\\b=72\\c=36\end{matrix}\right.\)
Vậy ..

Gọi x,y,z (cây) lần lượt là số cây trồng được của ba lớp 7A, 7B và 7C ( x, y, z \(\in\) N*)
Do số cây trồng được của ba lớp 7A,7B,7C lần lượt tỉ lệ với 6 ; 4 ; 5 nên:
\(\dfrac{x}{6}=\dfrac{y}{4}=\dfrac{z}{5}\)
Do tổng số cây của lớp 7B và 7C trồng được nhiều hơn của lớp 7A là 15 cây nên:
\(y+z-x=15\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\dfrac{x}{6}=\dfrac{y}{4}=\dfrac{z}{5}=\dfrac{y+z-x}{4+5-6}=\dfrac{15}{3}=5\)
\(\Rightarrow\left\{{}\begin{matrix}x=5\cdot6=30\\y=5\cdot4=20\\z=5\cdot5=25\end{matrix}\right.\)
Vậy ...
#Đạt Đang Bận Thở
Gọi số cay trồng được của lớp 7A,7B,7C lần lượt là a,b,c
Theo đề, ta có: a/6=b/4=c/5
Áp dụng tính chất của DTSBN, ta được:
a/6=b/4=c/5=(a-c)/(6-5)=15
=>a=90; b=60; c=75

Gọi số cây trồng được của lớp 7A , 7B , 7C lần lượt là : \(x;y;z\)
Ta có tỉ lệ \(\dfrac{x}{6}=\dfrac{y}{4}=\dfrac{z}{5}\)
Tổng số cây lớp 7B và 7C nhiều hơn lớp 7A là 15 cây
\(\Rightarrow y+z-x=15\)
Theo tính chất dãy tỉ số bằng nhau
\(\dfrac{x}{6}=\dfrac{y}{4}=\dfrac{z}{5}=\dfrac{y+z-x}{4+5-6}=\dfrac{15}{3}=5\\ \Rightarrow\left\{{}\begin{matrix}x=5.6=30\\y=4.5=20\\z=5.5=25\end{matrix}\right.\)
Vậy lớp 7A trồng được 30 cây , 7B trồng được 20 cây , 7C trồng được 25 cây
Gọi ba lớp `7A;7B;7C` tham gia trồng cây lần lượt là `a,b,c` `( a,b,c ∈ N)`
Theo bài ra ta có : `a/6=b/4=c/5` và `b+c-a=15`
ADTC dãy tỉ số bằng nhau ta có :
` a/6=b/4=c/5=(b+c-a)/(4+5-6)=15/3=5`
`=>a/6=5=>a=5.6=30`
`=>b/4=5=>b=5.4=20`
`=>c/5=5=>c=5.5=25`
Vậy ba lớp `7A;7B;7C` tham gia trồng cây lần lượt được `30;20;25` ( cây ) .

Gọi số cây mà `3` lớp trồng được lần lượt là `x,y,z (x,y,z \in \text {N*})`
Vì số cây của `3` lớp lần lượt tỉ lệ với `3:4:5`
Nghĩa là: `x/3=y/4=z/5`
Số cây trồng được của lớp `7A, 7B` nhiều hơn lớp `7C` là `40` cây
`-> x+y-z=40`
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
`x/3=y/4=z/5=(x+y-z)/(3+4-5)=40/2=20`
`-> x/3=y/4=z/5=20`
`-> x=20*3=60, y=20*4=80, z=20*5=100`
Vậy, số cây của `3` lớp lần lượt là `60` cây, `80` cây, `100` cây.
Gọi số cây trồng được của 3 lớp 7A,7B,7C lần lượt là \(x,y,z\)(cây) \((x,y,z \in N*)\)
Do số cây trồng được của 3 lớp 7A,7B,7C lần lượt tỉ lệ với 3,4,5 nên:\(\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{z}{5}\)
Do số cây trồng được của 2 lớp 7A,7B nhiều hơn số cây trồng được của lớp 7C là 40 cây nên \(x+y-z=40\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{z}{5}=\dfrac{x+y-z}{3+4-5}=\dfrac{40}{2}=20\)
Do đó:
\(\dfrac{x}{30}=20\Rightarrow x=60\)
\(\dfrac{y}{4}=20\Rightarrow y=80\) \(\left(TM\right)\)
\(\dfrac{z}{5}=20\Rightarrow z=100\)

Gọi số cây lớp 7A,7B,7C trồng được lần lượt là a(cây), b(cây),c(cây)
(Điều kiện: \(a\in Z^+;b\in Z^+;c\in Z^+\))
Số cây của lớp 7A,7B,7C lần lượt tỉ lệ với 6;4;5 nên ta có:
\(\dfrac{a}{6}=\dfrac{b}{4}=\dfrac{c}{5}\)
Tổng số cây trồng được của 2 lớp 7A,7B nhiều hơn của lớp 7C là 50 cây nên ta có: a+b-c=50
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{6}=\dfrac{b}{4}=\dfrac{c}{5}=\dfrac{a+b-c}{6+4-5}=\dfrac{50}{5}=10\)
=>a=60;b=40;c=50
Vậy: Lớp 7A trồng được 60 cây
Lớp 7B trồng được 40 cây
Lớp 7C trồng được 50 cây

Gọi số cây của ba lớp 7A ; 7B ; 7C lần lượt là a ; b và c ( cây ) ( a , b , c ∈ N* )
Theo bài ra , ta có :
b + c - a = 15
\(\frac{a}{6}=\frac{b}{4}=\frac{c}{5}\)
Áp dụng tính chất dãy tỉ số bằng nhau , ta có :
\(\frac{a}{6}=\frac{b}{4}=\frac{c}{5}=\frac{b+c-a}{4+5-6}=\frac{15}{3}=5\)
\(\Rightarrow\hept{\begin{cases}a=5.6=30\\b=5.4=20\\c=5.5=25\end{cases}}\)

Gọi số cây lớp 7A,7B,7C trồng được lần lượt là a,b,c
Theo đề, ta có: a/6=b/4=c/5 và a+b-c=50
Áp dụng tính chất của DTSBN, ta đc:
\(\dfrac{a}{6}=\dfrac{b}{4}=\dfrac{c}{5}=\dfrac{a+b-c}{6+4-5}=\dfrac{50}{5}=10\)
=>a=60; b=40; c=50
\(\text{Gọi số cây lớp 7A; 7B; 7C trồng đc lần lượt là x; y; z}\)\(\text{Theo đề bài, ta có: }\)
\(\dfrac{x}{4}=\dfrac{y}{6}=\dfrac{z}{3}\)
\(\text{Áp dụng tính chất của hai dãy tỷ số bằng nhau, ta có:}\)
\(\dfrac{x}{4}=\dfrac{y}{6}=\dfrac{z}{3}=\dfrac{\left(x+z\right)-y}{\left(4+3\right)-6}=\dfrac{12}{1}=12\)
\(\left\{{}\begin{matrix}\dfrac{x}{4}=12;x=12.4=48\\\dfrac{y}{6}=12;y=12.6=72\\\dfrac{z}{3}=12;z=12.3=36\end{matrix}\right.\)
\(\text{Vậy số cây của 3 lớp 7A; 7B; 7C trồng đc lần lượt là 48; 72; 36}\)
\(\text{Nếu thấy hay thì cho xin cái li.ke nha bn ôi}\)