Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi a,b,c (triệu đồng) lần lượt là số tiền lãi của 3 đơn vị (0 < a, b, c < 450).
Tổng số tiền lãi là 450 triệu đồng nên a+b+c = 450
Vì số tiền lãi tỉ lệ thuận với số vốn đã góp nên ta có:
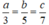
Theo tính chất của dãy tỉ số bằng nhau ta có:
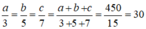
a/3 = 30 ⇒ a = 3.30 = 90
b/5 = 30 ⇒ b = 5.30 = 150
c/7 = 30 ⇒ c = 7.30 = 210
Vậy số tiền lãi được chia cho các đơn vị theo thứ tự là 90 triệu; 150 triệu và 210 triệu

Đơn vị thứ nhất nhận được số tiền lãi là :
450:(3+5+7)x3=90 triệu đồng
Đơn vị thứ hai nhận được số tiền lãi là :
450:(3+5+7)x5=150 triệu đồng
Đơn vị thứ ba nhận được số tiền lãi là :
450-150-90=210 triệu đồng
Đ/S:Đơn vị thứ nhất :90 triệu
Đơn vị thứ hai :150 triệu
Đơn vị thứ ba :210 triệu

Gọi số tiền lãi mà ba đơn vị được chia là x, y, z
Theo đề bài ta có:
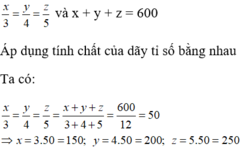
Chọn đáp án D

Gọi số tiền lãi sau 1 năm của 3 đơn vị lần lượt là a,b,c
Ta có : \(a:b:c=3:5:7\)
\(\Rightarrow\dfrac{a}{3}=\dfrac{b}{5}=\dfrac{c}{7}\)
Áp dụng tính chất dãy tỉ số bằng nhau, t/c
\(\Rightarrow\dfrac{a}{3}=\dfrac{b}{5}=\dfrac{c}{7}=\dfrac{a+b+c}{3+5+7}=\dfrac{225}{15}=15\)
\(\Rightarrow a=15.3=45\left(tr\right)\)
\(\Rightarrow b=15.5=75\left(tr\right)\)
\(\Rightarrow c=15.7=105\left(tr\right)\)
Vậy số tiền lãi của ba đơn vị sau 1 năm lần lượt là 45, 75 và 105 triệu đồng
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{3}=\dfrac{b}{5}=\dfrac{c}{7}=\dfrac{a+b+c}{3+5+7}=\dfrac{225000000}{15}=15000000\)
Do đó: a=45000000; b=75000000; c=105000000

Gọi số tiền lãi sau một năm tỉ lệ thuận với 3;5;7 là x;y;z.
\(\frac{x}{3}=\frac{y}{5}=\frac{z}{7}\) và \(x+y+z=225\)( triệu )
Áp dụng tính chất của dãy tỉ số bằng nhau:
\(\frac{x}{3}=\frac{y}{5}=\frac{z}{7}=\frac{z+y+z}{3+5+7}=\frac{225}{15}=15\)
\(\hept{\begin{cases}\frac{x}{3}=15\Rightarrow x=15.3=45\\\frac{y}{5}=15\Rightarrow y=15.5=75\\\frac{z}{7}=15\Rightarrow z=15.7=105\end{cases}}\)
Vậy tiền lãi của 3 đơn vị kinh doanh sau 1 năm lần lượt là: 45;75;105 ( triệu )
Tổng số phần bằng nhau là:
3 + 5 + 7 = 15 ( phần )
Đơn vị 1 được lãnh:
225 000 000 : 15 x 3 = 45 000 000đ
Đon vị 2 được lãnh:
225 000 000 : 15 x 5 = 75 000 000đ
Đơn vị 3 được lãnh:
225 000 000 : 15 x 7 = 105 000 000đ
Mình chỉ biết làm theo cách tiểu học thôi

Gọi số tiền vốn lần lượt là a,b,c(đồng)
Đk:a,b,c<450
a,b,c thuộc N*
Theo bài ra, ta có:
a/3=b/5=c/7 và a+b+c=450
Theo tính chất dãy tỉ số bằng nhau, ta có:
a/3=b/5=c/7=a+b+c/3+5+7=450/15=30
Với:
a/3=30=>a=3.30=90
b/5=30=>b=5.30=150
c/7=30=>c=7.30=210

gọi 3 đơn vị kinh doanh là x y z
x/3 = y/5 = z/7 x+y+z=450 tr
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
x/3 = y/5 = z/7 ; x/3+y/5+z/7 = 450/15 =30
x=30*3=60
y=30*5=150
z=30*7=350
vậy 3 đơn vị kinh doanh góp số vốn lần lượt là 60;150;350
like cho mik nha!

Gọi số tiền lãi của đơn vị 1 là a, số tiền lãi của đơn vị 2 là b, số tiền lãi của đơn vị 3 là c (triệu;a,b,c > 0)
Vì số tiền lãi được chia tỉ lệ thuận với số vốn đã góp
=>a:b:c=2:4:7
=>a/2=b/4=c/7
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có
a/2=b/4=c/7=a+b+c/2+4+7=177000000/13
Vì a/2=177000000/13 => a=(177000000/13).2 => a=354000000/13
Vì b/4=177000000/13 => b=(177000000/13).4 => b=708000000/13
Vì c/7=177000000/13 => c=(177000000/13).7 => c=1239000000/13
Vậy ...
Gọi vốn kinh doanh lần lượt là a, b, c ( a, b, c > 0)
Tổng số tiền lãi là 177 triệu đồng: a+b+c=177 triệu đồng.
Ba đơn vị vốn kinh doanh theo tỉ lệ 2, 4, 7 ta có:
a/2 = b/4 = c/7
theo t/c dãy tỉ số bằng nhau:
a/2 = b/4 = c/7 = a+b+c/2+4+7=177/13=...( tự biết kết quả )
Do đó:a=....( kết quả bên t/c dãy tỉ số bằng nhau ) . 2 = .....( tự làm )
b=....( kết quả bên trên t/c dãy tỉ số bằng nhau) . 4 = .....( tự làm )
c=....( kết quả bên trên t/c dãy tỉ số bằng nhau) . 7 = .....( tự làm )
Vậy:.....
Lần lượt là: 192 triệu, 320 triệu, 448 triệu
gọi số tiền lãi mà mỗi đơn vị nhận được lần lượt là x,y,z
ta có :
\(\hept{\begin{cases}x+y+z=960\text{ triệu}\\\frac{x}{3}=\frac{y}{5}=\frac{z}{7}\end{cases}}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có :
\(\frac{x}{3}=\frac{y}{5}=\frac{z}{7}=\frac{x+y+z}{3+5+7}=\frac{960}{15}=64\)
\(\Rightarrow\hept{\begin{cases}x=3\times64=192\text{ triệu}\\y=5\times64=320\text{ triệu}\\z=7\times64=448\text{ triệu}\end{cases}}\)