Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A C D B F E G I H O H'
a) Nối 2 điểm O và I
Vì 3 điểm H, O, I cùng nằm trên đường tròn có đường kính OH
\(\Rightarrow\) \(\Delta HIO\) nội tiếp đường tròn đường kính OH (1)
Mà OH là cạnh của \(\Delta HIO\) đồng thời cũng là đường kính (2)
Từ (1), (2) \(\Rightarrow\Delta HIO\) vuông tại I
\(\Rightarrow OI\perp HI\)
\(\Rightarrow OI\) cũng vuông góc với dây CD (3)
\(\Rightarrow IC=ID\left(4\right)\)
Ta lại có: BE \(\perp CD\left(gt\right)\left(5\right)\)
Từ (3), (5) \(\Rightarrow OI\)// BE
\(\Rightarrow OI\)// BF (6)
Mà OA = OB = R (gt) (7)
Từ (6), (7) \(\Rightarrow IA=IF\left(8\right)\)
Từ (4), (8) \(\Rightarrow ADFC\) là hình bình hành (9)
b) Từ (9) \(\Rightarrow FC=AD\left(10\right)\)
Và FC // AD
\(\Rightarrow\) \(\widehat{ICF}=\widehat{IDA}\) (2 góc so le trong) (11)
Từ (10), (11) \(\Rightarrow\Delta EFC=\Delta GAD\) (cạnh huyền - góc nhọn)
\(\Rightarrow CE=DG\) (2 cạnh tương ứng)
c) Nối 2 điểm F và H'
Ta có: HA = HO (gt) (12)
Từ (8), (12) \(\Rightarrow HI\) là đường trung bình của \(\Delta OAF\)
\(\Rightarrow HI\)// OF
\(\Rightarrow CD\)// OF (13)
Từ (5), (13) \(\Rightarrow BE\perp OF\)
\(\Rightarrow\Delta OBF\) vuông tại F (14)
Mà HO = H'O (gt) (15)
Từ (12) \(\Rightarrow HA=HO=\dfrac{1}{2}OA\left(16\right)\)
Từ (15), (16) \(\Rightarrow H'O=\dfrac{1}{2}OA\left(17\right)\)
Từ (7), (17) \(\Rightarrow H'O=\dfrac{1}{2}OB\left(18\right)\)
Mà H'O + H'B = OB
\(\Leftrightarrow\dfrac{1}{2}OB+H'B=OB\)
\(\Leftrightarrow H'B=OB-\dfrac{1}{2}OB\)
\(\Leftrightarrow H'B=\dfrac{1}{2}OB\) (19)
Từ (18), (19) \(\Rightarrow H'O=H'B\) (20)
Từ (14) \(\Rightarrow OB\) là cạnh huyền
Từ (20) \(\Rightarrow\) H' là trung điểm cạnh huyền OB của tam giác vuông OBF
\(\Rightarrow H'\)là tâm của đường tròn ngoại tiếp tam giác vuông OBF

Vị trí tương đối của hai đường tròn (O ; R) và (O’ ; r) (R ≥ r) | Hệ thức giữa OO’ với R và r | Số điểm chung | |
|---|---|---|---|
Hai đường tròn cắt nhau | R – r < OO’ < R + r | 2 | |
Hai đường tròn tiếp xúc nhau | - Tiếp xúc ngoài | OO’ = R + r | 1 |
- Tiếp xúc trong | OO’ = R – r > 0 | ||
Hai đường tròn không giao nhau | - (O) và (O’) ở ngoài nhau | OO’ > R + r | 0 |
- (O) đựng (O’) | OO’ < R - r |
Còn lại phần cuối 0 bên phải nhá Ly yêu?

Bài giải:
Thực hiện phép tính và điền vào chỗ trống ta được bảng sau:
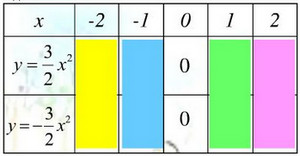
Vẽ đồ thị:
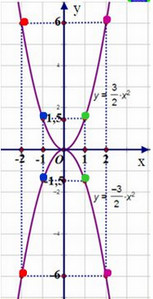
Nhận xét: Đồ thị của hai hàm số đối xứng với nhau qua trục Ox.
Xem thêm tại: http://loigiaihay.com/bai-4-trang-36-sgk-toan-9-tap-2-c44a5695.html#ixzz4dH45gBuO

+ (O;R) đựng (O';r)(O′;r) có số điểm chung là 0; hệ thức giữa d,R,rd,R,r là d = R - r
+ (O;R) và (O';r)(O′;r) ở ngoài nhau có 0 điểm chung, hệ thức giữa d,R,rd,R,r là d > R + r
+ (O;R) và (O';r)(O′;r) Tiếp xúc ngoài có 1 điểm chung, hệ thức giữa d,R,rd,R,r là d = R + r
+ (O;R) và (O';r)(O′;r) Tiếp xúc trong có 1 điểm chung, hệ thức giữa d,R,rd,R,r là d = R - r
+ (O;R) và (O';r)(O′;r) cắt nhau có 2 điểm chung, hệ thức giữa d,R,rd,R,r là d < R + r
0; d<R-r
Ở ngoài nhau;0
1;d=R+r
Tiếp xúc trong;1
Cắt nhau;R-r<d<R+r

1. Vì BO vuông góc với BA => góc ABO = 90 độ
Vi CO vuông góc với CA => góc ACO = 90 độ
Xét tứ giác ABOC có : Góc ABC = 90 độ, Góc ACO = 90 độ
mà 2 góc trên đối nhau và có tổng = 180 độ
=> tứ giác ABOC là tứ giác nội tiếp đường tròn.
Nối A với O, ta được tam giác ABO vuông tại B.
Vẽ trung tuyến BI của tam giác ABO => IO = IA = IB
=> I là tâm đường tròn ngoại tiếp tứ giác ABOC.
2. Câu này câu hỏi là gì vậy?
3,


@Nguyễn Việt Lâm
@Phạm Lan Hương
@Nguyễn Ngọc Lộc