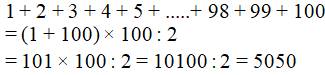Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Số số hạng của dãy số là 9(số);
=> Tổng của dãy số là (9+1)*9/2=45
b,Số số hạng của dãy số là 50 số
=> Tổng của dãy số là (50+1)*50/2=1275
c, Số số hạng của dãy số là (99-1)/2+1=50 số
=> Tổng của dãy số là (99+1)*50/2= 2500


Dãy số tự nhiên từ 1 đến 100 có số các số hạng là:
(100 - 1) : 1 + 1 = 100 (số)
100 số tạo thành số cặp là:
100 : 2 = 50 (cặp)
Ta có: 1 + 2 + 3 + 4 + 5 +....... + 96 + 97 + 98 + 99 + 100
= (1 + 100) + (2 + 99) + (3 + 98) + (4 + 97) + (5 + 96) +.....
= 101 + 101 + 101 + 101 +101 +......
= 101 x 50 = 5050
số số hạng là:(100-1):1+1=100ssh
tổng là:(100+1)*100:2=đến đây bạn tự làm

\(A=\dfrac{1+3+5+7+...+99}{50}\)
Số lượng số hạng của tổng là:
\(\left(99-1\right):2+1=50\)
Giá trị của A là:
\(A=\dfrac{\left(99+1\right)\cdot50:2}{50}=50\)
_____________________
\(B=\dfrac{2+4+6+..+98}{49}\)
Số lượng số hạng của tổng:
\(\left(98-2\right):2+1=49\) (số hạng)
Giá trị của B là:
\(B=\dfrac{\left(98+2\right)\cdot49:2}{49}=50\)
Vậy: A = B

a) \(A=98+\frac{1}{2}+\frac{1}{3}+...+\frac{1}{99}\)(có 98 phân số nên ta cộng 1 vào mỗi phân số)
\(A=\left(\frac{1}{2}+1\right)+\left(\frac{1}{3}+1\right)+...+\left(\frac{1}{99}+1\right)\)
\(A=\frac{3}{2}+\frac{4}{3}+...+\frac{100}{99}\)
Và \(B=\frac{3}{2}+\frac{4}{3}+...+\frac{100}{99}\)
\(\Rightarrow\frac{A}{B}=\frac{\frac{3}{2}+\frac{4}{3}+...+\frac{100}{99}}{\frac{3}{2}+\frac{4}{3}+...+\frac{100}{99}}=1\)
b) \(A=2018+\frac{1}{2}+\frac{1}{3}+...+\frac{1}{2019}\)(có 2018 phân số nên ta cộng 1 vào mỗi phân số)
\(A=\left(\frac{1}{2}+1\right)+\left(\frac{1}{3}+1\right)+...+\left(\frac{1}{2019}+1\right)\)
\(A=\frac{3}{2}+\frac{4}{3}+...+\frac{2020}{2019}\)
Và \(B=\frac{3}{2}+\frac{4}{3}+...+\frac{2020}{2019}\)
\(\Rightarrow\frac{A}{B}=\frac{\frac{3}{2}+\frac{4}{3}+...+\frac{2020}{2019}}{\frac{3}{2}+\frac{4}{3}+...+\frac{2020}{2019}}=1\)
c) \(A=\frac{99}{1}+\frac{98}{2}+...+\frac{1}{99}\)
\(A=99+\frac{98}{2}+...+\frac{1}{99}\)(có 98 phân số nên ta cộng 1 vào từng phân số)
\(A=\left(\frac{98}{2}+1\right)+\left(\frac{97}{3}+1\right)+...+\left(\frac{1}{99}+1\right)+1\)
\(A=\frac{100}{2}+\frac{100}{3}+...+\frac{100}{99}+1\)
\(A=100\left(\frac{1}{2}+\frac{1}{3}+...+\frac{1}{99}+\frac{1}{100}\right)\)
Và \(B=\frac{1}{2}+\frac{1}{3}+...+\frac{1}{99}+\frac{1}{100}\)
\(\Rightarrow\frac{A}{B}=\frac{100\left(\frac{1}{2}+\frac{1}{3}+...+\frac{1}{99}+\frac{1}{100}\right)}{\frac{1}{2}+\frac{1}{3}+...+\frac{1}{99}+\frac{1}{100}}=100\)
a)\(B=\frac{3}{2}+\frac{4}{3}+\frac{5}{4}+...+\frac{100}{99}\)
\(B=\left(1+\frac{1}{2}\right)+\left(1+\frac{1}{3}\right)+\left(1+\frac{1}{4}\right)+...+\left(1+\frac{1}{99}\right)\)
\(\Rightarrow B=\left(1+1+1+...+1\right)+\left(\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+...+\frac{1}{99}\right)\)
\(\Rightarrow B=98+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+...+\frac{1}{99}\)
\(\Rightarrow A:B=\frac{A}{B}=\frac{98+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+...+\frac{1}{99}}{98+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+...+\frac{1}{99}}=1.\)
Vậy \(A:B=1.\)
b)\(B=\left(1+\frac{1}{2}\right)+\left(1+\frac{1}{3}\right)+\left(1+\frac{1}{4}\right)+...+\left(1+\frac{1}{2019}\right)\)
\(\Rightarrow B=\left(1+1+1+...+1\right)+\left(\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+...+\frac{1}{2019}\right)\)
\(\Rightarrow B=2018+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+...+\frac{1}{2019}\)
\(\Rightarrow A:B=\frac{A}{B}=\frac{2018+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+...+\frac{1}{2019}}{2018+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+...+\frac{1}{2019}}=1.\)
Vậy \(A:B=1.\)
c)\(A=\left(1+1+...+1\right)+\frac{98}{2}+\frac{97}{3}+...+\frac{2}{98}+\frac{1}{99}\)
\(A=\left(1+\frac{98}{2}\right)+\left(1+\frac{97}{3}\right)+...+\left(1+\frac{2}{98}\right)+\left(1+\frac{1}{99}\right)\)
\(A=\frac{100}{2}+\frac{100}{3}+...+\frac{100}{98}+\frac{100}{99}\)
\(A=100\left(\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+...+\frac{1}{98}+\frac{1}{99}\right)\)
\(\Rightarrow A:B=\frac{A}{B}=\frac{100\left(\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+...+\frac{1}{98}+\frac{1}{99}\right)}{\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+...+\frac{1}{98}+\frac{1}{99}}=1.\)
Vậy \(A:B=1.\)

số số hạng là :
(100 - 1) + 1=100 (số)
Tổng là :
( 100 + 1 )x 100 : 2 = 5050

tổng trên bằng:
1-3+2-4+...+97-99+98-100=-2+-2+...+-2+-2
=(-2)x50=-100