Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn đáp án C.
Tần số ánh sáng không phụ thuộc vào môi trường, nghĩa là khi ánh sáng truyềntừ môi trường này sang môi trường khác thì tần số không đổi.
Vì λ ' = λ n = λ 1 , 52 < λ .
\(\lambda = c.T = c/f => f = \frac{c}{\lambda } =5.10^{14}Hz.\)
\(\lambda = v.T = v/f=> v = \lambda.f = 600.10^{-9}.5.10^{13}=3.10^7m/s.\)
= 720 nm, ánh sáng tím có bước sóng 
= 400 nm. Cho hai ánh sáng này truyền trong một môi trường trong suốt thì chiết suất tuyệt đối của môi trường đó đối với hai ánh sáng này lần lượt là n1 = 1,33 và n2 = 1,34. Khi truyền trong môi trường trong suốt trên, tỉ số năng lượng của phôtôn có bước sóng 
so với năng lượng của phôtôn có bước sóng 
bằng
+ Khi truyền từ môi trường này sang môi trường kia thì tần số của photon không đổi.
Mà ε = hf nên tỉ số năng lượng trong các môi trường cũng chính là tỉ số năng lượng trong chân không.
+ 
→ 
-
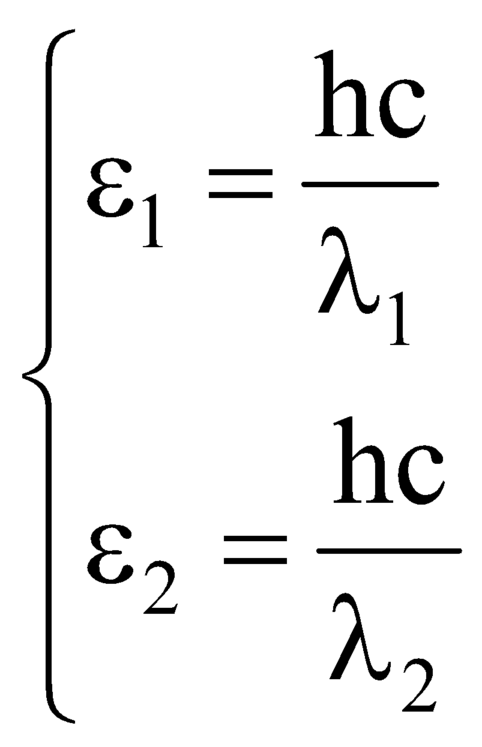
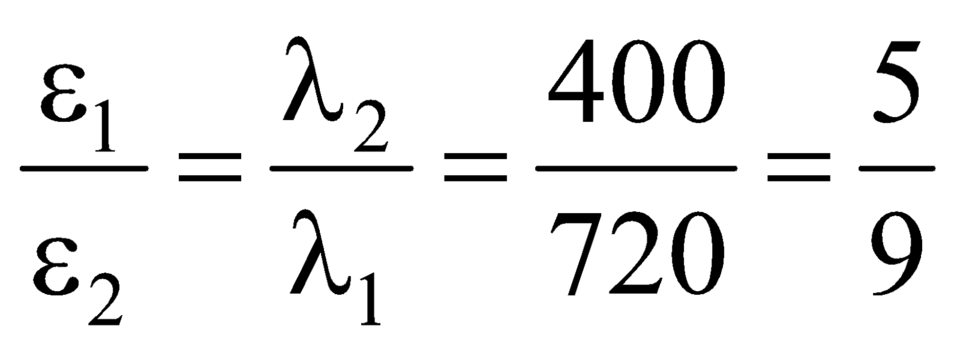
Đáp án A
Đáp án A
+ Vận tốc của ánh sang trong chân không là c = 3.10 8 m/s
+ Ánh sang có tần số không đổi trong mọi môi trường → vận tốc trong môi trường đó v = λ f = 2.10 8 m/s.
+ Chiết suất của môi trường đó là n = c v = 3 2 = 1 , 5
cách 1 : f = => f1=
= 3,95.1014Hz; f2=
= 7,89.1014Hz. Chọn A.
cách 2 : Trong chân không: ánh sáng nhìn thấy có tần số từ
= 3,85.1014 (Hz) đến
= 7,89.1014 (Hz). Đáp án A.
cách 3 : : Đáp án A.
\(\lambda = c.T= c/f=> f = \frac{c}{\lambda}.\)
\(f_{min}= \frac{c}{\lambda_{max}} = 3,947.10^{14}Hz.\)
\(f_{max}= \frac{c}{\lambda_{min}} = 7,895.10^{14}Hz.\)
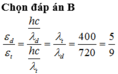
C.vẫn bằng 5.1014 Hz còn bước sóng nhỏ hơn 600 nm.
Ánh sáng đơn sắc khi truyền từ chân không sang môi trường có chiết suất n thì tần số không thay đổi và bước sóng bị giảm n lần.