
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(12,ĐK:x,y\ne0\\ HPT\Leftrightarrow\left\{{}\begin{matrix}\dfrac{4}{x}+\dfrac{2}{y}=4\\\dfrac{6}{x}-\dfrac{2}{y}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{10}{x}=5\\\dfrac{2}{x}+\dfrac{1}{y}=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\\dfrac{1}{y}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\left(tm\right)\)
\(13,\Leftrightarrow\left\{{}\begin{matrix}3\left(x+1\right)+2\left(x+2y\right)=4\\8\left(x+1\right)-2\left(x+2y\right)=18\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}11\left(x+1\right)=22\\3\left(x+1\right)+2\left(x+2y\right)=4\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=1\\6+2+4y=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-1\end{matrix}\right.\)
\(14,ĐK:x+y\ne0;y\ne1\\ HPT\Leftrightarrow\left\{{}\begin{matrix}\dfrac{4}{x+y}+\dfrac{1}{y-1}=5\\\dfrac{4}{x+y}-\dfrac{8}{y-1}=-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{x+y}-\dfrac{2}{y-1}=-1\\\dfrac{9}{y-1}=9\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{x+2}=1\\y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+2=1\\y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=2\end{matrix}\right.\left(tm\right)\)
\(15,ĐK:x\ge-1\\ HPT\Leftrightarrow\left\{{}\begin{matrix}2\left(x+y\right)+\sqrt{x+1}=4\\2\left(x+y\right)-6\sqrt{x+1}=-10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}7\sqrt{x+1}=14\\2\left(x+y\right)+\sqrt{x+1}=4\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=3\left(tm\right)\\6+2y+2=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=-2\end{matrix}\right.\left(tm\right)\)
\(16,ĐK:x\ne1;y\ne-2\\ HPT\Leftrightarrow\left\{{}\begin{matrix}\dfrac{3x}{x-1}-\dfrac{2}{y+2}=4\\\dfrac{4x}{x-1}+\dfrac{2}{y+2}=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{7x}{x-1}=14\\\dfrac{2x}{x-1}+\dfrac{1}{y+2}=5\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=2\\\dfrac{1}{y+2}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=-1\end{matrix}\right.\left(tm\right)\)
\(17,ĐK:x\ge0;y\ge1\\ HPT\Leftrightarrow\left\{{}\begin{matrix}\sqrt{x}+2\sqrt{y-1}=5\\8\sqrt{x}-2\sqrt{y-1}=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}9\sqrt{x}=9\\\sqrt{x}+2\sqrt{y-1}=5\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=1\\\sqrt{y-1}=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=5\end{matrix}\right.\)
\(18,\Leftrightarrow\left\{{}\begin{matrix}8x-2\left|y+2\right|=6\\x+2\left|y+2\right|=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}9x=9\\x+2\left|y+2\right|=3\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=1\\\left|y+2\right|=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\\left[{}\begin{matrix}y=-1\\y=-3\end{matrix}\right.\end{matrix}\right.\\ 20,ĐK:y\ne1\\ HPT\Leftrightarrow\left\{{}\begin{matrix}2x+\dfrac{3}{y-1}=5\\12x-\dfrac{3}{y-1}=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}14x=14\\2x+\dfrac{3}{y-1}=5\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=1\\\dfrac{3}{y-1}=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=2\end{matrix}\right.\left(tm\right)\)
\(21,ĐK:x\ne-1\\ HPT\Leftrightarrow\left\{{}\begin{matrix}\dfrac{9}{x+1}-6y=-3\\\dfrac{10}{x+1}+6y=22\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{19}{x+1}=19\\\dfrac{3}{x+1}-2y=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\3-2y=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=2\end{matrix}\right.\left(tm\right)\)


a: Thay \(x=9+4\sqrt{2}\) vào A, ta được:
\(A=\dfrac{2\sqrt{2}+1+7}{2\sqrt{2}+1-1}=\dfrac{8+2\sqrt{2}}{2\sqrt{2}}=2\sqrt{2}+1\)

Lời giải:
$\Delta'=(m+1)^2-(2m-3)=m^2+4>0$ với mọi $m$ nên pt luôn có 2 nghiệm pb với mọi $m$
Áp dụng định lý Viet:
$x_1+x_2=2(m+1)$
$x_1x_2=2m-3$
Để $x_1<1<x_2$
$\Leftrightarrow (x_1-1)(x_2-1)<0$
$\Leftrightarrow x_1x_2-(x_1+x_2)+1<0$
$\Leftrightarrow 2m-3-2(m+1)+1<0$
$\Leftrightarrow -3-2+1<0$
$\Leftrightarrow -4<0$ (luôn đúng)
Vậy PT luôn có 2 nghiệm pb thỏa mãn đề với mọi $m\in\mathbb{R}$

x2-(m-1)x+m-2=0(1)
Để phương trình có hai nghiệm phân biệt thì Δ=(-m+1)2-4(m-2)
=m2-2m+1-4m+8
=m2-6m+9
=(m-3)2≥0 với mọi m
⇒phương trình luôn có hai nghiệm phân biệt
Áp dụng định lý Vi-ét ta có:\(\begin{cases} x_1+x_2=m-2 \\ x_1.x_2=m-1 \end{cases}\)(2)
TH1:x1,x2 là hai cạnh góc vuông
⇒x1=x2
Từ (2)\(\begin{cases} x_1+x_1=m-2 \\ x_1^2=m-1 \end{cases}\)
\(\Leftrightarrow\)\(\begin{cases} x_1=\frac{m-1}{2}\\ x_1=\sqrt{m-2} \end{cases}\)
\(\Leftrightarrow\)\(\dfrac{m-1}{2}\)=\(\sqrt{m-2}\)
\(\Leftrightarrow\)\(\dfrac{m^2-2m+1}{4}\)=m-2
\(\Leftrightarrow\)m2-6m+9=0
\(\Leftrightarrow\)(m-3)2=0
\(\Leftrightarrow\)m=3
TH2:x1 là cạnh huyền,x2 là cạnh góc vuông
⇒x1=\(\sqrt{2}\)x2
Từ (2)⇒\(\begin{cases} \sqrt{2} x_2+x_2=m-1 \\ \sqrt{2} x_2^2=m-2 \end{cases}\)
\(\Leftrightarrow\)\(\begin{cases} x_2= \frac{m-1}{1+\sqrt{2}} \\ x_2=\sqrt{\frac{m-2}{\sqrt{2}}} \end{cases}\)
\(\Leftrightarrow\)\(\dfrac{m-1}{1+\sqrt{2}}\)=\(\sqrt{\dfrac{m-2}{\sqrt{2}}}\)
\(\Leftrightarrow\)\(\dfrac{m^2-2m+1}{3+2\sqrt{2}}\)=\(\dfrac{m-2}{\sqrt{2}}\)
\(\Leftrightarrow\)\(\left(3+2\sqrt{2}\right)\)\(m\)\(-6-2\sqrt{2}\)\(=\sqrt{2}m^2-2\sqrt{2}m+\sqrt{2}\)
\(\Leftrightarrow\sqrt{2}m^2-\left(4\sqrt{2}+3\right)m+3\sqrt{2}+6=0\)
\(\Leftrightarrow\)rồi m bằng bao nhiêu thì tự giải nhé mệt r

\(\Delta=25-4\left(m-1\right)=29-4m>0\Rightarrow m< \dfrac{29}{4}\)
Khi đó theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=5\\x_1x_2=m-1\end{matrix}\right.\)
\(2x_1=\sqrt{x_2}\Rightarrow\left\{{}\begin{matrix}x_1;x_2\ge0\\4x_1^2=x_2=5-x_1\end{matrix}\right.\)
\(\Rightarrow4x_1^2+x_1-5=0\Rightarrow\left[{}\begin{matrix}x_1=1\\x_1=-\dfrac{5}{4}< 0\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow x_2=4x_1^2=4\)
Thế vào \(x_1x_2=m-1\Rightarrow m-1=4\Rightarrow m=5\)


\(a,m=3\Leftrightarrow y=2x+2\\ A\left(a;-4\right)\in\left(d\right)\Leftrightarrow2a+2=-4\Leftrightarrow a=-3\)
\(b,\) PT giao Ox của (d) là \(2x+m-1=0\Leftrightarrow x=\dfrac{1-m}{2}\Leftrightarrow M\left(\dfrac{1-m}{2};0\right)\Leftrightarrow OM=\dfrac{\left|1-m\right|}{2}\)
PT giao Oy của (d) là \(x=0\Leftrightarrow y=m-1\Leftrightarrow N\left(0;m-1\right)\Leftrightarrow ON=\left|m-1\right|\)
Để \(S_{OMN}=1\Leftrightarrow\dfrac{1}{2}OM\cdot ON=1\Leftrightarrow OM\cdot ON=2\)
\(\Leftrightarrow\dfrac{\left|\left(1-m\right)\left(m-1\right)\right|}{2}=2\\ \Leftrightarrow\left|-\left(m-1\right)^2\right|=2\\ \Leftrightarrow\left(m-1\right)^2=2\\ \Leftrightarrow\left[{}\begin{matrix}m=1+\sqrt{2}\\m=1-\sqrt{2}\end{matrix}\right.\)

Câu 3:
Thay x=-1 và y=0 vào (d), ta được:
-m+2m-1=0
hay m=1


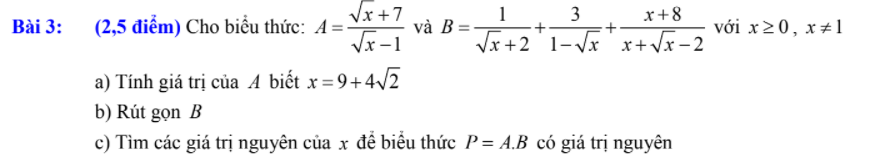 được không ạ, mai em phải nộp rồi, cảm ơn mn nhiều.
được không ạ, mai em phải nộp rồi, cảm ơn mn nhiều. 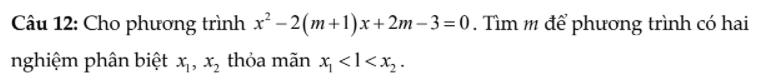
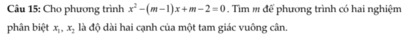
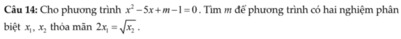


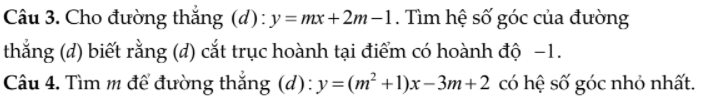 này được
này được