
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\Rightarrow P=\left(\dfrac{\left(y-x\right)\left(y+x\right)}{y-x}-\dfrac{\left(x-y\right)\left(x^2+xy+y^2\right)}{\left(x-y\right)\left(x+y\right)}\right).\dfrac{x+y}{y^2-2xy+x^2+xy}\)
\(\Rightarrow P=\left(y+x-\dfrac{x^2+xy+y^2}{x+y}\right).\dfrac{x+y}{y^2-xy+x^2}\)
\(\Rightarrow P=\dfrac{\left(x+y\right)^2-\left(x^2+xy+y^2\right)}{x+y}.\dfrac{x+y}{y^2-xy+x^2}\)
\(\Rightarrow P=\dfrac{x^2+2xy+y^2-x^2-xy-y^2}{x+y}.\dfrac{x+y}{y^2-xy+x^2}\)
\(\Rightarrow P=\dfrac{xy}{x+y}.\dfrac{x+y}{y^2-xy+x^2}\)
\(\Rightarrow P=\dfrac{xy}{y^2-xy+x^2}\)

a: Ta có: \(3\left(x-2\right)^2+\left(x-1\right)^3-x^3=-7\)
\(\Leftrightarrow3x^2-12x+12+x^3-3x^2+3x-1-x^3=-7\)
\(\Leftrightarrow-9x=-18\)
hay x=2
b: ta có: \(\left(x+2\right)^3-x\left(x-1\right)\left(x+1\right)=6x^2-5x+3\)
\(\Leftrightarrow x^3+6x^2+12x+8-x^3+x-6x^2+5x-3=0\)
\(\Leftrightarrow17x=-5\)
hay \(x=-\dfrac{5}{17}\)
c: Ta có: \(\left(2x-1\right)^3+12\left(x-1\right)\left(x+1\right)=14x-13\)
\(\Leftrightarrow8x^3-12x^2+6x-1+12x^2-12-14x+13=0\)
\(\Leftrightarrow8x^3-8x=0\)
\(\Leftrightarrow8x\left(x-1\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\\x=-1\end{matrix}\right.\)
a) \(3\left(x-2\right)^2+\left(x-1\right)^3-x^3=-7\)
\(\Rightarrow3x^2-12x+12+x^3-3x^2+3x-1-x^3=-7\)
\(\Rightarrow-9x=-18\)
\(\Rightarrow x=2\)
b) \(\left(x+2\right)^3-x\left(x-1\right)\left(x+1\right)=6x^2-5x+3\)
\(\Rightarrow x^3+6x^2+12x+8-x^3+x=6x^2-5x+3\)
\(\Rightarrow18x=-5\)
\(\Rightarrow x=-\dfrac{5}{18}\)
c) \(\left(2x-1\right)^3+12\left(x-1\right)\left(x+1\right)=14x-13\)
\(\Rightarrow8x^3-12x^2+6x-1+12x^2-12=14x-13\)
\(\Rightarrow8x^3-8x=0\)
\(\Rightarrow8x\left(x-1\right)\left(x+1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=1\\x=-1\end{matrix}\right.\)

Bài 2:
a: Ta có: \(A=\left(x^2-3x+5\right)-\left(x^2+4x-1\right)+5x^2-3\)
\(=x^2-3x+5-x^2-4x+1+5x^2-3\)
\(=5x^2-7x+3\)
b: Ta có: \(B=\left(3x^2-11x+7\right)-\left(2x^2+3x+4\right)\)
\(=3x^2-11x+7-2x^2-3x-4\)
\(=x^2-14x+3\)

\(\left(x+3\right)\left(x^2-3x+3^2\right)-x\left(x^2-3\right)\)
\(=x^3+3^3-x^3-3x\)
\(=3^3-3x\)
\(=3\left(3^2-x\right)\)
\(\left(x+3\right)\left(x^2-3x+9\right)-x\left(x^2-3\right)\)
\(=x^3+3^3-x^3+3x\)
\(=27+3x\)
\(=3\left(9+x\right)\)


mình tìm không tháy bạn ơi ~ chủ yếu là mình nhờ mấy bạn từng học qua rồi chỉ giúp những dạng chủ yếu,mẹo vặt các loại đấy bạn !! không phải mình tìm đề đâu ~~`

22 + 11 bằng 33
Bọn mik chuẩn bị tiết mục văn nghệ r

\(\left(x-1\right)^3-x\left(x-1\right)^2=5x\left(2-x\right)-11\left(x+2\right)\)
\(\Leftrightarrow x^3-3x^2+3x-1-x^3+2x^2-x=10x-5x^2-11x-22\)
\(\Leftrightarrow-x^2+2x-1=-5x^2-x-22\)
\(\Leftrightarrow4x^2+3x+21=0\)
Ta có \(\Delta=3^2-4.4.21< 0\)
Vậy pt vô nghiệm
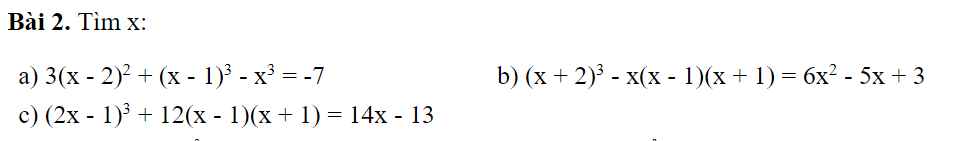 giúp với em sắp phải nộp deadline r ạ:((
giúp với em sắp phải nộp deadline r ạ:((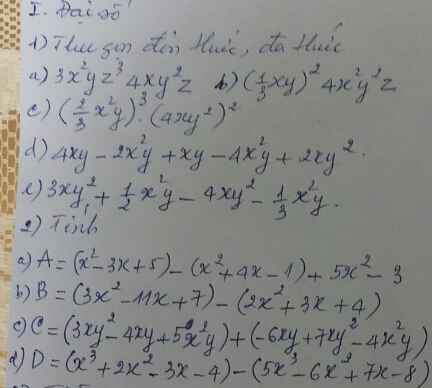
\(P=\dfrac{x^3-y^3}{x^2y-xy^2}-\dfrac{x^3+y^3}{x^2y+xy^2}-\left(\dfrac{x}{y}-\dfrac{y}{x}\right)\left(\dfrac{x+y}{x-y}-\dfrac{x-y}{x+y}\right)\)
\(=\dfrac{\left(x-y\right)\left(x^2+xy+y^2\right)}{xy\left(x-y\right)}-\dfrac{\left(x+y\right)\left(x^2-xy+y^2\right)}{xy\left(x+y\right)}-\dfrac{x^2-y^2}{xy}\cdot\dfrac{x^2+2xy+y^2-x^2+2xy-y^2}{\left(x-y\right)\left(x+y\right)}\)
\(=\dfrac{x^2+xy+y^2-x^2+xy-y^2}{xy}-\dfrac{\left(x-y\right)\left(x+y\right)}{xy}\cdot\dfrac{4xy}{\left(x-y\right)\left(x+y\right)}\)
\(=2-4=-2\)