Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b, PT giao điểm (d3) và (d1) là \(\dfrac{1}{3}x+3=2x-2\Leftrightarrow\dfrac{5}{3}x=5\Leftrightarrow x=3\Leftrightarrow y=4\Leftrightarrow A\left(3;4\right)\)
PT giao điểm (d3) và (d2) là \(\dfrac{1}{3}x+3=-\dfrac{4}{3}x-2\Leftrightarrow\dfrac{5}{3}x=-5\Leftrightarrow x=-3\Leftrightarrow y=2\Leftrightarrow B\left(-3;2\right)\)

Phương trình hoành độ giao điểm của (d1) và (d3):
2x – 2 = (1/3).x + 3 ⇔ 2x - (1/3).x = 3 + 2 ⇔ (5/3).x = 5 ⇔ x = 3
Tung độ giao điểm: y = 2.3 – 2 ⇔ y = 6 – 2 = 4
Vậy tọa độ điểm A là A(3; 4)
Phương trình hoành độ giao điểm của ( d 2 ) và ( d 3 ):
- (4/3).x – 2 = (1/3).x + 3 ⇔ (1/3).x + (4/3).x = -2 – 3 ⇔ (5/3).x = -5 ⇔ x = -3
Tung độ giao điểm: y = (1/3).(-3) + 3 ⇔ y = -1 + 3 = 2
Vậy tọa độ điểm B là B(-3; 2)

a/ Bạn tự vẽ
b/ Ta lập pt hoành độ giao điểm :
(d1) giao với (d2) : \(-x-5=\frac{1}{4}x\Leftrightarrow x=-4\) thay vào (d1) được y = -1
Vậy A(-4;-1) . Tương tự ta tìm được điểm B(-1;-4)
c/ Ta có : \(AB=\sqrt{\left(x_B-x_A\right)^2+\left(y_B-y_A\right)^2}=\sqrt{\left(-1+4\right)^2+\left(-4+1\right)^2}=3\sqrt{2}\)
\(OA=\sqrt{x_A^2+y_A^2}=\sqrt{4^2+1^2}=\sqrt{17}\) ; \(OB=\sqrt{x_B^2+y_B^2}=\sqrt{1^2+4^2}=\sqrt{17}\)
=> OAB là tam giác cân
d/ Gọi OH là đường cao hạ từ O xuống AB (H thuộc AB)
Vì tam giác OAB cân tại O nên AH = HB = 1/2AB = \(\frac{3\sqrt{2}}{2}\)
\(OH=\sqrt{OA^2-BH^2}=\sqrt{17-\left(\frac{3\sqrt{2}}{2}\right)^2}=\frac{5\sqrt{2}}{2}\)
\(S_{ABC}=\frac{1}{2}AB.OH=\frac{1}{2}.3\sqrt{2}.\frac{5\sqrt{2}}{2}=\frac{15}{2}\)

\(a,\) Bn tự vẽ
\(b,\) PT hoành độ giao điểm của \(\left(d_1\right);\left(d_2\right)\) là
\(-\dfrac{1}{2}x=\dfrac{1}{2}x+3\\ \Leftrightarrow x=-3\\ \Leftrightarrow y=-\dfrac{1}{2}\left(-3\right)=\dfrac{3}{2}\)
Vậy tọa độ giao điểm \(\left(d_1\right);\left(d_2\right)\) là \(A\left(-3;\dfrac{3}{2}\right)\)
\(c,\) Gọi \(B\left(m;-m\right)\) là tọa độ giao điểm của \(\left(d_2\right);\left(d_3\right)\)
\(\Leftrightarrow-m=\dfrac{1}{2}m+3\Leftrightarrow\dfrac{3}{2}m=3\\ \Leftrightarrow m=2\)
Vậy tọa độ giao điểm của \(\left(d_2\right);\left(d_3\right)\) là \(B\left(2;-2\right)\)
Khi đó \(-2=2\cdot2+b\Leftrightarrow b=-6\)

a:
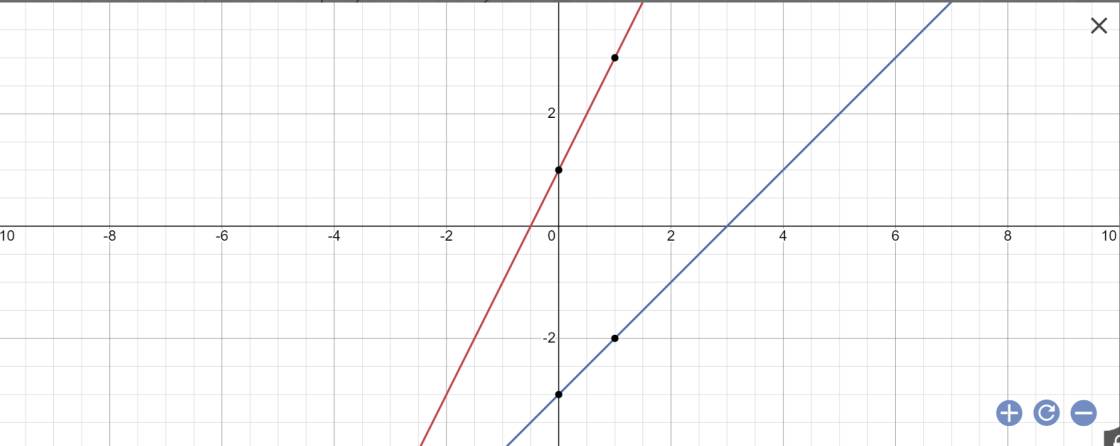
b: Phương trình hoành độ giao điểm là:
\(2x+1=x-3\)
=>\(2x-x=-3-1\)
=>x=-4
Thay x=-4 vào y=x-3, ta được:
\(y=-4-3=-7\)
Vậy: Tọa độ giao điểm của (D1) và (D2) là B(-4;-7)
c: Đặt phương trình đường thẳng (d3): y=ax+b
Vì (d3)//(d1) nên \(\left\{{}\begin{matrix}a=2\\b< >1\end{matrix}\right.\)
Vậy: y=2x+b
Thay x=1 và y=0 vào y=2x+b, ta được:
\(b+2\cdot1=0\)
=>b+2=0
=>b=-2
Vậy: (d): y=2x-2
a: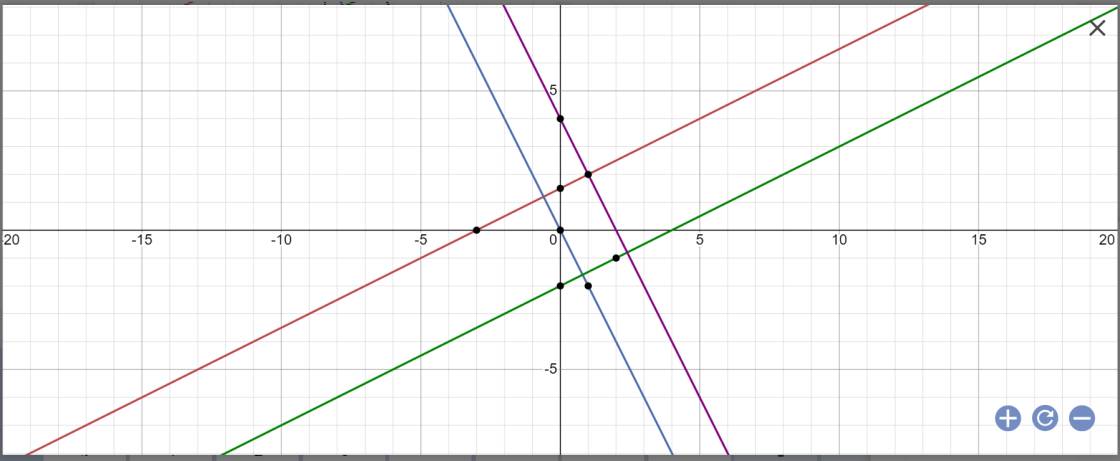
b: (d1): y=1/2x+3/2; (d2): y=-2x; (d3): y=1/2x-2; (d4): y=-2x+4
=>(d1) vuông góc (d2), (d1) vuông góc (d4); (d2) vuông góc (d3); (d2)//(d4)
=>ABCD là hình chữ nhật
=>A(-3/5;6/5); B(2/5;16/5); C(4/5;-8/5); D(12/5;-4/5)