Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(AB=\dfrac{BH}{\sin A}=\dfrac{1,5}{\sin30^0}=3\left(cm\right)\)
Do đó \(P_{ABCD}=4AB=12\left(cm\right)\)

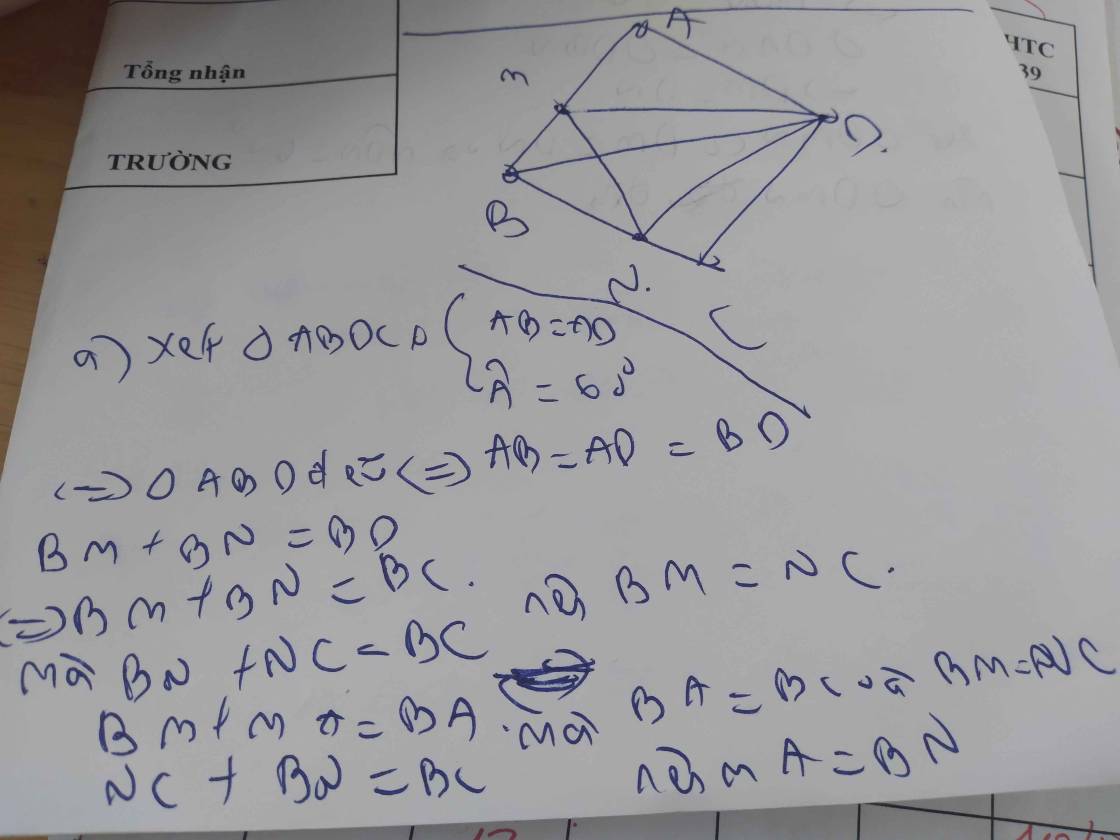
A B C D M N H 60 1 1 2
Nối DM, DN
Trên cạnh AD lấy H sao cho AH = AM
\(\Delta\) AHM có AH = AM (cách vẽ) nên \(\Delta\) AHM cân tại A (đn)
\(\Delta\) AHM cân tại A có góc A = 60o (gt) nên \(\Delta\) AHM đều
=> MH = AM = AH
ABCD là hình thoi (gt) nên AB = BC = CD = AD (đn)
AB = BC <=> BN + NC = BM + AM = AB
Mà BM + BN = AB (gt)
Do đó, BM = NC, AM = BN = MH
AB = AD (cmt) <=> BM + AM = AH + HD
Mà AM = AH (cách vẽ)
Do đó, BM = HD
ABCD là hình thoi (gt) nên AD // BC (t/c)
=> góc A + góc B = 180o (trong cùng phía)
<=> 60o + góc B = 180o
<=> góc B = 120o
\(\Delta AMH\) đều (cmt) nên góc AHM = 60o
Lại có: AHM + MHD = 180o (kề bù)
Do đó, MHD = 120o
\(\Delta MBN=\Delta DHM\left(c.g.c\right)\)=> MN = MD (2 cạnh t/ứ)
và góc N1 = góc M1
Lại có: N1 + M2 = 60o (tự c/m)
Do đó, M1 + M2 = 60o
=> góc DMN = 60o
\(\Delta\) DMN cân tại M (vì MN = MD) có DMN = 60o (cmt) nên tam giác DMN đều
=> đường trung trực của MN đi qua D
Mà D cố định do hình thoi ABCD cố định nên ta có đpcm