Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
\(\dfrac{1}{1.2.3}+\dfrac{1}{2.3.4}+...+\dfrac{1}{10.11.12}=\dfrac{1}{1.2}-\dfrac{1}{2.3}+\dfrac{1}{2.3}-\dfrac{1}{3.4}+....+\dfrac{1}{10.11}-\dfrac{1}{11.12}=\dfrac{1}{1.2}-\dfrac{1}{11.12}=\dfrac{1}{2}-\dfrac{1}{132}=\dfrac{65}{132}\)Mà \(\dfrac{65}{132}\ne\dfrac{1}{4}\Rightarrow\) Có thể bạn ghi sai đề thì phải !

\(A=\dfrac{3}{4}\cdot\dfrac{8}{9}\cdot\dfrac{15}{16}\cdot...\cdot\dfrac{899}{900}\)
\(A=\dfrac{1\cdot3}{2\cdot2}\cdot\dfrac{2\cdot4}{3\cdot3}\cdot\dfrac{3\cdot5}{4\cdot4}\cdot...\cdot\dfrac{29\cdot31}{30\cdot30}\)
\(A=\dfrac{1\cdot\left(2\cdot3\cdot4\cdot5\cdot...\cdot29\right)^2\cdot30\cdot31}{\left(2\cdot3\cdot4\cdot...\cdot30\right)^2}\)
\(A=\dfrac{1\cdot\left(2\cdot3\cdot4\cdot5\cdot...\cdot29\right)^2\cdot30\cdot31}{\left(2\cdot3\cdot4\cdot5\cdot...\cdot29\right)^2\cdot30\cdot30}\)
\(A=\dfrac{1\cdot31}{30}=\dfrac{31}{30}\)
Ta có : \(\dfrac{1}{101}>\dfrac{1}{300}\)
...
\(\dfrac{1}{299}>\dfrac{1}{300}\)
Do đó :
\(\dfrac{1}{101}+\dfrac{1}{102}+..+\dfrac{1}{300}>\dfrac{1}{300}+\dfrac{1}{300}..+\dfrac{1}{300}\)
\(\Rightarrow\dfrac{1}{101}+\dfrac{1}{102}+..+\dfrac{1}{300}>\dfrac{200}{300}=\dfrac{2}{3}\)
Vậy...

\(\dfrac{1}{1.2.3}+\dfrac{1}{2.3.4}+...+\dfrac{1}{10.11.12}\)
\(=\dfrac{1}{2}\left(\dfrac{2}{1.2.3}+\dfrac{2}{2.3.4}+...+\dfrac{2}{10.11.12}\right)\)
\(=\dfrac{1}{2}.\left(\dfrac{1}{1.2}-\dfrac{1}{2.3}+\dfrac{1}{2.3}-\dfrac{1}{3.4}+...+\dfrac{1}{10.11}-\dfrac{1}{11.12}\right)\)
\(=\dfrac{1}{2}.\left(\dfrac{1}{1.2}-\dfrac{1}{11.12}\right)\)
\(=\dfrac{1}{2}.\left(\dfrac{1}{2}-\dfrac{1}{132}\right)\)
\(=\dfrac{1}{2}.\dfrac{65}{132}\)
\(=\dfrac{65}{264}\)
Vậy...

* Chứng tỏ
Ta có :\(\dfrac{1}{1.2.3}+\dfrac{1}{2.3.4}+\dfrac{1}{3.4.5}+...+\dfrac{1}{98.99.100}\)
= \(\dfrac{1}{1.2.3}.\dfrac{2}{2}+\dfrac{1}{2.3.4}.\dfrac{2}{2}+...+\dfrac{1}{98.99.100}.\dfrac{2}{2}\)
= \(\dfrac{1}{2}.\left(\dfrac{2}{1.2.3}+\dfrac{2}{2.3.4}+\dfrac{2}{3.4.5}+...+\dfrac{2}{98.99.100}\right)\)
= \(\dfrac{1}{2}.\left(\dfrac{1}{1.2}-\dfrac{1}{2.3}+\dfrac{1}{2.3}-\dfrac{1}{3.4}+...+\dfrac{1}{98.99}-\dfrac{1}{99.100}\right)\)
= \(\dfrac{1}{2}.\left(\dfrac{1}{1.2}+0+0+...+0+\dfrac{-1}{99.100}\right)\)
= \(\dfrac{1}{2}.\left(\dfrac{1}{2}+\dfrac{-1}{9900}\right)\)
= \(\dfrac{1}{2}.\left(\dfrac{4850}{9900}+\dfrac{-1}{9900}\right)\)
= \(\dfrac{1}{2}.\dfrac{4849}{9900}\)
= \(\dfrac{4849}{19800}\)

Ta có :
\(\dfrac{1}{1.2}-\dfrac{1}{2.3}=\dfrac{3}{1.2.3}-\dfrac{1}{1.2.3}=\dfrac{2}{1.2.3}\)
\(\dfrac{1}{2.3}-\dfrac{1}{3.4}=\dfrac{4}{2.3.4}-\dfrac{2}{2.3.4}=\dfrac{2}{2.3.4}\)
...
Do đó :
\(\dfrac{1}{1.2.3}=\dfrac{1}{2}\left(\dfrac{1}{1.2}-\dfrac{1}{2.3}\right)\)
\(\dfrac{1}{2.3.4}=\dfrac{1}{2}\left(\dfrac{1}{2.3}-\dfrac{1}{3.4}\right)\)
Vậy :
\(M=\dfrac{1}{2}\left(\dfrac{1}{1.2}-\dfrac{1}{2.3}+\dfrac{1}{2.3}-\dfrac{1}{3.4}+\dfrac{1}{3.4}-\dfrac{1}{4.5}+...+\dfrac{1}{10.11}-\dfrac{1}{11.12}\right)\)
\(=\dfrac{1}{2}\left(\dfrac{1}{1.2}-\dfrac{1}{11.12}\right)\)
\(=\dfrac{1}{2}\left(\dfrac{1}{2}-\dfrac{1}{132}\right)\)
\(=\dfrac{1}{2}.\dfrac{65}{132}=\dfrac{65}{264}\)

A= \(\dfrac{1}{1.2.3}+\dfrac{1}{2.3.4}+\dfrac{1}{4.5.6}+....+\dfrac{1}{37.38.39}\)
A=\(\dfrac{1}{1}-\dfrac{1}{39}\)
A=\(\dfrac{38}{39}\)
còn lại tự làm do mình có việc chút

hôm qua cô giảng cho mình bài này không cần tính đâu
Gọi tổng là A
A=\(\dfrac{1}{1.2.3}+\dfrac{1}{2.3.4}+...+\dfrac{1}{17.18.19}\)
2A=\(\dfrac{2}{1.2.3}+\dfrac{2}{2.3.4}+...+\dfrac{2}{17.18.19}\)
2A=\(\dfrac{1}{1.2}-\dfrac{1}{2.3}+\dfrac{1}{2.3}-\dfrac{1}{3.4}+...+\dfrac{1}{17.18}-\dfrac{1}{18.19}\)
2A=\(\dfrac{1}{2}-\dfrac{1}{18.19}\)
A=\(\dfrac{1}{2}.\left(\dfrac{1}{2}-\dfrac{1}{18.19}\right)\)
A=\(\dfrac{1}{2}.\dfrac{18.19-2}{2.18.19}\) < \(\dfrac{1}{4}\)
A=\(\dfrac{18.19-2}{2.2.18.19}\) < \(\dfrac{18.19}{2.2.18.19}\)
\(\Rightarrow\) A<\(\dfrac{1}{4}\)
\(\dfrac{1}{1.2.3}\)+\(\dfrac{1}{2.3.4}\)+\(\dfrac{1}{3.4.5}\)+...+\(\dfrac{1}{17.18.19}\)<\(\dfrac{1}{4}\)
Đặt A=\(\dfrac{1}{1.2.3}\)+\(\dfrac{1}{2.3.4}\)+\(\dfrac{1}{3.4.5}\)+...+\(\dfrac{1}{17.18.19}\)
2.A=2.(\(\dfrac{1}{1.2.3}\)+\(\dfrac{1}{2.3.4}\)+\(\dfrac{1}{3.4.5}\)+...+\(\dfrac{1}{17.18.19}\))
2. A=\(\dfrac{2}{1.2.3}\)+\(\dfrac{2}{2.3.4}\)+\(\dfrac{2}{3.4.5}\)+...+\(\dfrac{2}{17.18.19}\)
2.A=\(\dfrac{1}{1.2}\)-\(\dfrac{1}{2.3}\)+\(\dfrac{1}{2.3}\)-\(\dfrac{1}{3.4}\)+ ...+\(\dfrac{1}{17.18}\)-\(\dfrac{1}{18.19}\)
2.A=\(\dfrac{1}{1.2}\)-\(\dfrac{1}{18.19}\)=\(\dfrac{85}{171}\)
A=\(\dfrac{85}{171}\):2=\(\dfrac{85}{342}\)
Ta cũng có: \(\dfrac{1}{4}\) = \(\dfrac{171}{684}\); \(\dfrac{85}{342}\) = \(\dfrac{170}{684}\)
Vì 170 < 171 ( \(\dfrac{170}{684}\) < \(\dfrac{171}{684}\) )
Vậy \(\dfrac{1}{1.2.3}+\dfrac{1}{2.3.4}+\dfrac{1}{3.4.5}+...+\dfrac{1}{17.18.19}\) < \(\dfrac{1}{4}\)

\(\dfrac{1}{2}\left(\dfrac{1}{1.2}+\dfrac{1}{2.3}+...+\dfrac{1}{18.19}+\dfrac{1}{19.20}\right)\) Gio thi tu ma lam ko thích viết nữa mệt
bn ơi mk nghĩ bn nên tôn trọng mk một chút! Nếu bn giúp đc thì mk cảm ơn rất nhiều. Còn bn không làm đc thì để cho người khác làm! bn ko thích làm thì mk cx ko mong bn giải nửa chừng như vậy, mk vừa ko hiểu j mà còn bị tự ái khi bn nói như vậy, mong bn hiểu!!mk góp ý thật lòng, ko chỉ đối với mk mà với những bn khác cx zậy!!

a, A= 1/2. (2/1.2.3+2/2.3.4+2/3.4.5+...+2/18.19.20) A=1/2. (1/1.2-1/2.3+1/2.3-1/3.4+1/3.4-1/4.5+...+1/18.19-1/19.20) A=1/2. (1/1.2-1/19.20) A=1/2. 189/380 A= 189/760
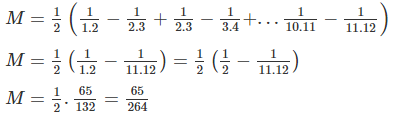
\(\dfrac{1}{1.2.3}\) + \(\dfrac{1}{2.3.4}\) + .....+ \(\dfrac{1}{10.11.12}\)
= \(\dfrac{1}{1.2}\) - \(\dfrac{1}{2.3}\) + \(\dfrac{1}{2.3}\) - \(\dfrac{1}{3.4}\) +....+ \(\dfrac{1}{10.11}\) - \(\dfrac{1}{11.12}\)
=\(\dfrac{1}{1.2}\) + (- \(\dfrac{1}{2.3}\) + \(\dfrac{1}{2.3}\))+.......+ ( \(-\dfrac{1}{10.11}\) + \(\dfrac{1}{10.11}\)) - \(\dfrac{1}{11.12}\)
=\(\dfrac{1}{2}\) - \(\dfrac{1}{11.12}\) =\(\dfrac{1}{2}\) - \(\dfrac{1}{132}\) =\(\dfrac{66}{132}\)-\(\dfrac{1}{132}\) =\(\dfrac{65}{132}\) Vì \(\dfrac{33}{132}\) = \(\dfrac{1}{4}\) nên \(\dfrac{65}{132}\) > \(\dfrac{1}{4}\)