Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

• Xét hàm số \(f\left( x \right) = 2x - \sin x\) có tập xác định \(D = \mathbb{R}\).
Vậy hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\).
• Xét hàm số \(g\left( x \right) = \sqrt {x - 1} \)
ĐKXĐ: \(x - 1 \ge 0 \Leftrightarrow x \ge 1\)
Hàm số \(g\left( x \right) = \sqrt {x - 1} \) có tập xác định \(D = \left[ {1; + \infty } \right)\).
Hàm số \(g\left( x \right) = \sqrt {x - 1} \) là hàm căn thức nên liên tục trên khoảng \(\left( {1; + \infty } \right)\).
Ta có: \(\mathop {\lim }\limits_{x \to {1^ + }} g\left( x \right) = \mathop {\lim }\limits_{x \to {1^ + }} \sqrt {x - 1} = \sqrt {1 - 1} = 0 = g\left( 1 \right)\)
Do đó hàm số \(g\left( x \right) = \sqrt {x - 1} \) liên tục tại điểm \({x_0} = 1\).
Vậy hàm số \(g\left( x \right) = \sqrt {x - 1} \) liên tục trên nửa khoảng \(\left[ {1; + \infty } \right)\).
• Xét hàm số \(y = f\left( x \right).g\left( x \right) = \left( {2x - \sin x} \right)\sqrt {x - 1} \)
Do hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) đều liên tục tại mọi điểm \({x_0} \in \left[ {1; + \infty } \right)\) nên hàm số \(y = f\left( x \right).g\left( x \right)\) liên tục trên nửa khoảng \(\left[ {1; + \infty } \right)\).
• Xét hàm số \(y = \frac{{f\left( x \right)}}{{g\left( x \right)}} = \frac{{2x - \sin x}}{{\sqrt {x - 1} }}\)
Do hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) đều liên tục tại mọi điểm \({x_0} \in \left[ {1; + \infty } \right)\) nên hàm số \(y = \frac{{f\left( x \right)}}{{g\left( x \right)}}\) liên tục trên khoảng \(\left( {1; + \infty } \right)\).

\(a,y'=\left(tanx\right)'=\left(\dfrac{sinx}{cosx}\right)'\\ =\dfrac{\left(sinx\right)'cosx-sinx\left(cosx\right)'}{cos^2x}\\ =\dfrac{cos^2x+sin^2x}{cos^2x}\\ =\dfrac{1}{cos^2x}\\ b,\left(cotx\right)'=\left[tan\left(\dfrac{\pi}{2}-x\right)\right]'\\ =-\dfrac{1}{cos^2\left(\dfrac{\pi}{2}-x\right)}\\ =-\dfrac{1}{sin^2\left(x\right)}\)

\(y'=\left(cosx\right)'\\ =\left(\dfrac{\pi}{2}-x\right)'cos\left(\dfrac{\pi}{2}-x\right)\\ =-cos\left(\dfrac{\pi}{2}-x\right)\\ =-sinx\)

a) Cách 1: Ta có:
y' = 6sin5x.cosx - 6cos5x.sinx + 6sinx.cos3x - 6sin3x.cosx = 6sin3x.cosx(sin2x - 1) + 6sinx.cos3x(1 - cos2x) = - 6sin3x.cos3x + 6sin3x.cos3x = 0.
Vậy y' = 0 với mọi x, tức là y' không phụ thuộc vào x.
Cách 2:
y = sin6x + cos6x + 3sin2x.cos2x(sin2x + cos2x) = sin6x + 3sin4x.cos2x + 3sin2x.cos4x + cos6x = (sin2x + cos2x)3 = 1
Do đó, y' = 0.
b) Cách 1:
Áp dụng công thức tính đạo hàm của hàm số hợp
(cos2u)' = 2cosu(-sinu).u' = -u'.sin2u
Ta được
y' =[sin - sin
] + [sin
- sin
] - 2sin2x = 2cos
.sin(-2x) + 2cos
.sin(-2x) - 2sin2x = sin2x + sin2x - 2sin2x = 0,
vì cos = cos
=
.
Vậy y' = 0 với mọi x, do đó y' không phụ thuộc vào x.
Cách 2: vì côsin của hai cung bù nhau thì đối nhau cho nên
cos2 = cos2
'
cos2 = cos2
.
Do đó
y = 2 cos2 + 2cos2
- 2sin2x = 1 +cos
+ 1 +cos
- (1 - cos2x) = 1 +cos
+ cos
+ cos2x = 1 + 2cos
.cos(-2x) + cos2x = 1 + 2
cos2x + cos2x = 1.
Do đó y' = 0.

Ta có: \(\mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}} = f'\left( {{x_0}} \right);\mathop {\lim }\limits_{x \to {x_0}} \frac{{g\left( x \right) - g\left( {{x_0}} \right)}}{{x - {x_0}}} = g'\left( {{x_0}} \right)\)
Vậy \(h'\left( {{x_0}} \right) = f'\left( {{x_0}} \right) + g'\left( {{x_0}} \right)\).

\(y'=\left[sin\left(\dfrac{\pi}{3}-3x\right)\right]'\\ =\left(\dfrac{\pi}{3}-3x\right)'cos\left(\dfrac{\pi}{3}-3x\right)\\ =-3cos\left(\dfrac{\pi}{3}-3x\right)\)

a: \(y'=\left(x^2+2x\right)'\left(x^3-3x\right)+\left(x^2+2x\right)\left(x^3-3x\right)'\)
\(=\left(2x+2\right)\left(x^3-3x\right)+\left(x^2+2x\right)\left(3x^2-3\right)\)
\(=2x^4-6x^2+2x^3-6x+3x^4-3x^2+6x^3-6x\)
\(=5x^4+8x^3-9x^2-12x\)
b: y=1/-2x+5
=>\(y'=\dfrac{2}{\left(2x+5\right)^2}\)
c: \(y'=\dfrac{\left(4x+5\right)'}{2\sqrt{4x+5}}=\dfrac{4}{2\sqrt{4x+5}}=\dfrac{2}{\sqrt{4x+5}}\)
d: \(y'=\left(sinx\right)'\cdot cosx+\left(sinx\right)\cdot\left(cosx\right)'\)
\(=cos^2x-sin^2x=cos2x\)
e: \(y=x\cdot e^x\)
=>\(y'=e^x+x\cdot e^x\)
f: \(y=ln^2x\)
=>\(y'=\dfrac{\left(-1\right)}{x^2}=-\dfrac{1}{x^2}\)


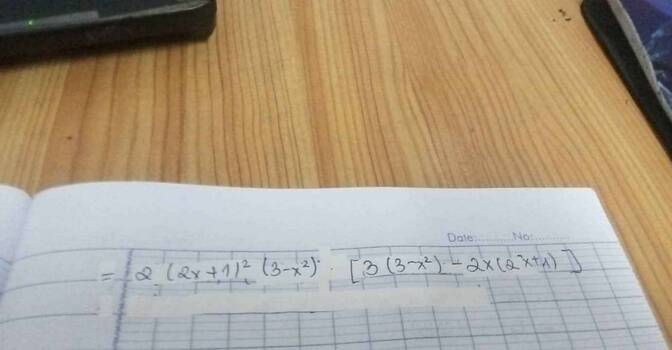
a) \(g'\left( x \right) = y' = {\left( {2x + \frac{\pi }{4}} \right)^,}.\cos \left( {2x + \frac{\pi }{4}} \right) = 2\cos \left( {2x + \frac{\pi }{4}} \right)\)
b) \(g'\left( x \right) = - 2{\left( {2x + \frac{\pi }{4}} \right)^,}.\sin \left( {2x + \frac{\pi }{4}} \right) = - 4\sin \left( {2x + \frac{\pi }{4}} \right)\)