Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét \(\Delta x\) là số gia của biến số tại điểm x
Ta có:
\(\begin{array}{l}\Delta y = f\left( {x + \Delta x} \right) - f\left( x \right) = {\left( {x + \Delta x} \right)^3} - {x^3} = \left( {x + \Delta x - x} \right)\left[ {x{{\left( {x + \Delta x} \right)}^2} + x.\left( {x + \Delta x} \right) + {x^2}} \right]\\ = \Delta x\left( {{x^2} + 2x.\Delta x + {{\left( {\Delta x} \right)}^2} + {x^2} + x.\Delta x + {x^2}} \right) = \Delta x.\left( {3{x^2} + {{\left( {\Delta x} \right)}^2} + 3x.\Delta x} \right)\\ \Rightarrow \frac{{\Delta y}}{{\Delta x}} = 3{x^2} + {\left( {\Delta x} \right)^2} + 3x.\Delta x\end{array}\)
Ta thấy:
\(\begin{array}{l}\mathop {\lim }\limits_{\Delta x \to 0} \frac{{\Delta y}}{{\Delta x}} = \mathop {\lim }\limits_{\Delta x \to 0} \left( {3{x^2} + {{\left( {\Delta x} \right)}^2} + 3x.\Delta x} \right) = 3{x^2}\\ \Rightarrow f'\left( x \right) = 3{x^2}\end{array}\)

a) Với bất kì \({x_0} \in \mathbb{R}\), ta có:
\(f'\left( {{x_0}} \right) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{\left( { - {x^2}} \right) - \left( { - x_0^2} \right)}}{{x - {x_0}}}\)
\( = \mathop {\lim }\limits_{x \to {x_0}} \frac{{ - \left( {{x^2} - x_0^2} \right)}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \frac{{ - \left( {x - {x_0}} \right)\left( {x + {x_0}} \right)}}{{x - {x_0}}}\)
\( = \mathop {\lim }\limits_{x \to {x_0}} \left( { - x - {x_0}} \right) = - {x_0} - {x_0} = - 2{{\rm{x}}_0}\)
Vậy \(f'\left( x \right) = {\left( { - {x^2}} \right)^\prime } = - 2x\) trên \(\mathbb{R}\).
b) Với bất kì \({x_0} \in \mathbb{R}\), ta có:
\(f'\left( {{x_0}} \right) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{\left( {{x^3} - 2{\rm{x}}} \right) - \left( {x_0^3 - 2{{\rm{x}}_0}} \right)}}{{x - {x_0}}}\)
\( = \mathop {\lim }\limits_{x \to {x_0}} \frac{{{x^3} - 2{\rm{x}} - x_0^3 + 2{{\rm{x}}_0}}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \frac{{\left( {{x^3} - x_0^3} \right) - 2\left( {x - {x_0}} \right)}}{{x - {x_0}}}\)
\( = \mathop {\lim }\limits_{x \to {x_0}} \frac{{\left( {x - {x_0}} \right)\left( {{x^2} + x.{x_0} + x_0^2} \right) - 2\left( {x - {x_0}} \right)}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \frac{{\left( {x - {x_0}} \right)\left( {{x^2} + x.{x_0} + x_0^2 - 2} \right)}}{{x - {x_0}}}\)
\( = \mathop {\lim }\limits_{x \to {x_0}} \left( {{x^2} + x.{x_0} + x_0^2 - 2} \right) = x_0^2 + {x_0}.{x_0} + x_0^2 - 2 = 3{\rm{x}}_0^2 - 2\)
Vậy \(f'\left( x \right) = {\left( {{x^3} - 2{\rm{x}}} \right)^\prime } = 3{{\rm{x}}^2} - 2\) trên \(\mathbb{R}\).
c) Với bất kì \({x_0} \ne 0\), ta có:
\(f'\left( {{x_0}} \right) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{\frac{4}{x} - \frac{4}{{{x_0}}}}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \frac{{\frac{{4{x_0} - 4x}}{{x{x_0}}}}}{{x - {x_0}}}\)
\( = \mathop {\lim }\limits_{x \to {x_0}} \frac{{4{x_0} - 4x}}{{x{x_0}\left( {x - {x_0}} \right)}} = \mathop {\lim }\limits_{x \to {x_0}} \frac{{ - 4\left( {x - {x_0}} \right)}}{{x{x_0}\left( {x - {x_0}} \right)}}\)
\( = \mathop {\lim }\limits_{x \to {x_0}} \frac{{ - 4}}{{x{{\rm{x}}_0}}} = \frac{{ - 4}}{{{x_0}.{x_0}}} = - \frac{4}{{x_0^2}}\)
Vậy \(f'\left( x \right) = {\left( {\frac{4}{x}} \right)^\prime } = - \frac{4}{{{x^2}}}\) trên các khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {0; + \infty } \right)\).

Hàm số \(f\left( x \right) = 2{x^3} + x + 1\) xác định trên \(\mathbb{R}\).
Ta có: \(\begin{array}{l}\mathop {\lim }\limits_{x \to 2} f\left( x \right) = \mathop {\lim }\limits_{x \to 2} \left( {2{x^3} + x + 1} \right) = {2.2^3} + 2 + 1 = 17\\f\left( 2 \right) = {2.2^3} + 2 + 1 = 17\\ \Rightarrow \mathop {\lim }\limits_{x \to 2} f\left( x \right) = f\left( 2 \right)\end{array}\)
Do đó hàm số liên tục tại x = 2.

a) Với \({x_0}\) bất kì, ta có:
\(f'\left( {{x_0}} \right) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \frac{{{x^3} - x_0^3}}{{x - {x_0}}}\\ = \mathop {\lim }\limits_{x \to {x_0}} \frac{{\left( {x - {x_0}} \right)\left( {{x^2} + x{x_0} + x_0^2} \right)}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \left( {{x^2} + x{x_0} + x_0^2} \right) = 3x_0^2\)
Vậy hàm số \(y = {x^3}\) có đạo hàm là hàm số \(y' = 3{x^2}\)
b) \(y' = \left( {{x^n}} \right)' = n{x^{n - 1}}\)

a/ \(y=\left(x^3-3x\right)^{\dfrac{3}{2}}\Rightarrow y'=\dfrac{3}{2}\left(x^3-3x\right)^{\dfrac{1}{2}}\left(x^3-3x\right)'=\dfrac{3}{2}\left(3x^2-3\right)\sqrt{x^3-3x}\)
b/ \(y'=5\left(\sqrt{x^3+1}-x^2+2\right)^4\left(\sqrt{x^3+1}-x^2+2\right)'=5\left(\sqrt{x^3+1}-x^2+2\right)^4\left(\dfrac{3x^2}{\sqrt{x^3+1}}-2x\right)\)c/
\(y'=14\left(x^6+2x-3\right)^6\left(x^6+2x-3\right)'=14\left(x^6+2x-3\right)^6\left(6x^5+2\right)\)
d/ \(y=\left(x^3-1\right)^{-\dfrac{5}{2}}\Rightarrow y'=-\dfrac{5}{2}\left(x^3-1\right)^{-\dfrac{7}{2}}\left(x^3-1\right)'=-\dfrac{15x^2}{2\sqrt{\left(x^3-1\right)^7}}\)

a: \(f'\left(x_0\right)=\lim\limits_{x\rightarrow x0}\dfrac{f\left(x\right)-f\left(x0\right)}{x-x0}=\lim\limits_{x\rightarrow x0}\dfrac{c-c}{x-x0}=0\)
b: \(f'\left(x0\right)=\lim\limits_{x\rightarrow x0}\dfrac{f\left(x\right)-f\left(x0\right)}{x-x0}=\lim\limits_{x\rightarrow x0}\dfrac{x-x0}{x-x0}=1\)


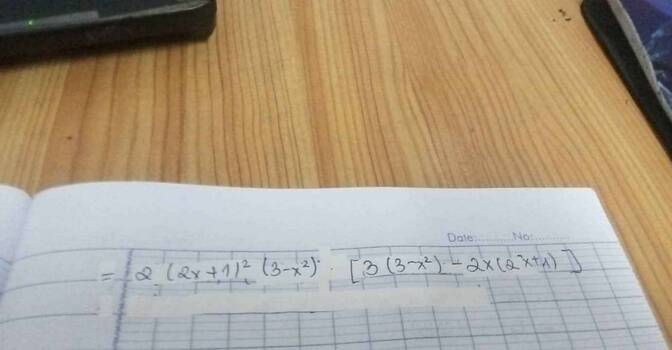
a) Với \({x_0}\) bất kì, ta có:
\(\begin{array}{l}f'\left( {{x_0}} \right) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \frac{{{x^3} + {x^2} - x_0^3 - x_0^2}}{{x - {x_0}}}\\ = \mathop {\lim }\limits_{x \to {x_0}} \frac{{\left( {x - {x_0}} \right)\left( {{x^2} + x{x_0} + x_0^2} \right) + \left( {x - {x_0}} \right)\left( {x + {x_0}} \right)}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \frac{{\left( {x - {x_0}} \right)\left( {{x^2} + x{x_0} + x_0^2 + x + {x_0}} \right)}}{{x - {x_0}}}\\ = \mathop {\lim }\limits_{x \to {x_0}} \left( {{x^2} + x{x_0} + x_0^2 + x + {x_0}} \right) = 3x_0^2 + 2{x_0}\end{array}\)
Vậy hàm số \(y = {x^3} + {x^2}\) có đạo hàm là hàm số \(y' = 3{x^2} + 2x\)
b) \({\left( {{x^3}} \right)^,} + {\left( {{x^2}} \right)^,} = 3{x^2} + 2x\)
Do đó \(\left( {{x^3} + {x^2}} \right)'\) = \(\left( {{x^3}} \right)' + \left( {{x^2}} \right)'.\)