Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có: \(\overrightarrow u = ({x_1};{y_1}),\;\overrightarrow v = ({x_2};{y_2}),\;\overrightarrow w = ({x_3};{y_3}).\)
\(\begin{array}{l} \Rightarrow \overrightarrow v + \overrightarrow w = ({x_2};{y_2}) + ({x_3};{y_3}) = \left( {{x_2} + {x_3};{y_2} + {y_3}} \right)\\ \Rightarrow \overrightarrow u .\left( {\overrightarrow v + \overrightarrow w } \right) = {x_1}.\left( {{x_2} + {x_3}} \right) + {y_1}.\left( {{y_2} + {y_3}} \right)\end{array}\)
Và: \(\;\overrightarrow u .\overrightarrow v + \overrightarrow u .\overrightarrow w = \left( {{x_1}.{x_2} + {y_1}.{y_2}} \right) + \left( {{x_1}.{x_3} + {y_1}.{y_3}} \right)\)\( = {x_1}.{x_2} + {y_1}.{y_2} + {x_1}.{x_3} + {y_1}.{y_3}.\)
b) Vì \({x_1}.{x_2} + {y_1}.{y_2} + {x_1}.{x_3} + {y_1}.{y_3}\)\( = \left( {{x_1}.{x_2} + {x_1}.{x_3}} \right) + \left( {{y_1}.{y_2} + {y_1}.{y_3}} \right)\)\( = {x_1}.\left( {{x_2} + {x_3}} \right) + {y_1}.\left( {{y_2} + {y_3}} \right)\)
Nên \(\overrightarrow u .\left( {\overrightarrow v + \overrightarrow w } \right) = \;\overrightarrow u .\overrightarrow v + \overrightarrow u .\overrightarrow w \)
c) Ta có: \(\overrightarrow u = ({x_1};{y_1}),\;\overrightarrow v = ({x_2};{y_2})\)
\( \Rightarrow \left\{ \begin{array}{l}\overrightarrow u .\overrightarrow v = {x_1}.{x_2} + {y_1}.{y_2}\\\overrightarrow v .\overrightarrow u = {x_2}.{x_1} + {y_2}.{y_1}\end{array} \right.\)\( \Leftrightarrow \;\overrightarrow u .\overrightarrow v = \overrightarrow v .\overrightarrow u \)

a) \(\overrightarrow{a}=2\overrightarrow{u}+3\overrightarrow{v}=2\left(3;-4\right)+3\left(2;5\right)=\left(6;-8\right)+\left(6;15\right)\)\(=\left(12;7\right)\).
b) \(\overrightarrow{b}=\overrightarrow{u}-\overrightarrow{v}=\left(3;-4\right)-\left(2;5\right)=\left(1;-9\right)\).
c) Hai véc tơ \(\overrightarrow{c}=\left(m;10\right)\) và \(\overrightarrow{v}\) cùng phương khi và chỉ khi:
\(\dfrac{m}{2}=\dfrac{10}{5}=2\Rightarrow m=4\).

a) Tọa độ vectơ \(\overrightarrow u = \left( {2.\left( { - 1} \right) + 3 - 3.2;2.2 + 1 - 3.\left( { - 3} \right)} \right) = \left( { - 5;14} \right)\)
b) Do \(\overrightarrow x + 2\overrightarrow b = \overrightarrow a + \overrightarrow c \Leftrightarrow \overrightarrow x = \overrightarrow a + \overrightarrow c - 2\overrightarrow b = \left( { - 1 + 2 - 2.3;2 + \left( { - 3} \right) - 2.1} \right) = \left( { - 5; - 3} \right)\)
Vậy \(\overrightarrow x = \left( { - 5; - 3} \right)\)

a) Vì \(\overrightarrow {OA} = \overrightarrow u = (x;y)\) nên A(x; y).
Tương tự: do \(\overrightarrow {OB} = \overrightarrow v = \left( {x';y'} \right)\) nên B (x’; y’)
b) Ta có: \(\overrightarrow {OA} = (x;y) \Rightarrow O{A^2} = {\left| {\overrightarrow {OA} } \right|^2} = {x^2} + {y^2}.\)
Và \(\overrightarrow {OB} = (x';y') \Rightarrow O{B^2} = {\left| {\overrightarrow {OB} } \right|^2} = x{'^2} + y{'^2}.\)
Lại có: \(\overrightarrow {AB} = \overrightarrow {OB} - \overrightarrow {OA} = \left( {x';y'} \right) - \left( {x;y} \right) = \left( {x' - x;y' - y} \right)\)
\( \Rightarrow A{B^2} = {\left| {\overrightarrow {AB} } \right|^2} = {\left( {x' - x} \right)^2} + {\left( {y' - y} \right)^2}.\)
c) Theo định lí cosin trong tam giác OAB ta có:
\(\cos \widehat O = \frac{{O{A^2} + O{B^2} - A{B^2}}}{{2.OA.OB}}\)
Mà \(\overrightarrow {OA} .\overrightarrow {OB} = \left| {\overrightarrow {OA} } \right|.\left| {\overrightarrow {OB} } \right|.\cos \left( {\overrightarrow {OA} ,\overrightarrow {OB} } \right) = OA.OB.\cos \widehat O\)
\( \Rightarrow \overrightarrow {OA} .\overrightarrow {OB} = OA.OB.\frac{{O{A^2} + O{B^2} - A{B^2}}}{{2.OA.OB}} = \frac{{O{A^2} + O{B^2} - A{B^2}}}{2}\)
\(\begin{array}{l} \Rightarrow \overrightarrow {OA} .\overrightarrow {OB} = \frac{{{x^2} + {y^2} + x{'^2} + y{'^2} - {{\left( {x' - x} \right)}^2} - {{\left( {y' - y} \right)}^2}}}{2}\\ \Leftrightarrow \overrightarrow {OA} .\overrightarrow {OB} = \frac{{ - \left( { - 2x'.x} \right) - \left( { - 2y'.y} \right)}}{2} = x'.x + y'.y\end{array}\)

a) \(\overrightarrow{u}=3\overrightarrow{a}+2\overrightarrow{b}-4\overrightarrow{c}=3\left(2;1\right)+2\left(3;-4\right)-4\left(-7;2\right)\)
\(=\left(6;3\right)+\left(6;-8\right)-\left(-28;8\right)\)
\(=\left(6+6+28;3-8-8\right)=\left(40;-13\right)\).
b) \(\overrightarrow{x}+\overrightarrow{a}=\overrightarrow{b}-\overrightarrow{c}\Leftrightarrow\overrightarrow{x}=\overrightarrow{b}-\overrightarrow{c}-\overrightarrow{a}\)
\(\Leftrightarrow\overrightarrow{x}=\left(3;-4\right)-\left(-7;2\right)-\left(2;1\right)\)
\(\Leftrightarrow\overrightarrow{x}=\left(3+7-2;-4-2-1\right)\)
\(\Leftrightarrow\overrightarrow{x}=\left(8;-7\right)\).
c) Có \(\overrightarrow{c}\left(-7;2\right)=k\overrightarrow{a}+h\overrightarrow{b}=k\left(2;1\right)+h\left(3;-4\right)\)
\(=\left(2k+3h;k-4h\right)\).
Từ đó suy ra: \(\left\{{}\begin{matrix}2k+3h=-7\\k-4h=2\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}k=-2\\h=-1\end{matrix}\right.\).

A. Ta có: \(\frac{2}{{\frac{1}{2}}} = 4 \ne \frac{3}{6}\) nên \(\overrightarrow u \) và \(\overrightarrow v \) không cùng phương.
B. Ta có: \(\frac{{\sqrt 2 }}{1} = \frac{6}{{3\sqrt 2 }} = \sqrt 2 > 0\) nên \(\overrightarrow a \) và \(\overrightarrow b \) cùng phương, hơn nữa là cùng hướng
Chọn đáp án B.
C. Ta có: \(\overrightarrow i .\overrightarrow j = 0.1 + 1.0 = 0 \Rightarrow \overrightarrow i \bot \overrightarrow j \)
Vậy \(\overrightarrow i \) và \(\overrightarrow j \) không cùng phương.
D. Ta có: \(\frac{1}{2} \ne \frac{3}{{ - 6}}\) nên \(\overrightarrow c \) và \(\overrightarrow d \) không cùng phương.

\(\overrightarrow{u}\left(2;3\right)=2\left(1;0\right)+3\left(0;1\right)=2\overrightarrow{i}+3\overrightarrow{j}\).
\(\overrightarrow{u}\left(-1;4\right)=-\left(1;0\right)+4\left(0;1\right)=-\overrightarrow{i}+4\overrightarrow{j}\).
\(\overrightarrow{u}\left(2;0\right)=2.\left(1;0\right)+0.\left(0;1\right)=2\overrightarrow{i}+0\overrightarrow{j}\).
\(\overrightarrow{u}\left(0;-1\right)=0.\left(1;0\right)-1.\left(0;1\right)=0\overrightarrow{i}-\overrightarrow{j}\).
\(\overrightarrow{u}\left(0;0\right)=0.\left(1;0\right)+0.\left(0;1\right)=0\overrightarrow{i}+0\overrightarrow{j}.\)

A. Ta có: \(\overrightarrow u .\overrightarrow v = 2.4 + 3.6 = 26 \ne 0\) nên \(\overrightarrow u \) và \(\overrightarrow v \) không vuông góc với nhau.
B. Ta có: \(\overrightarrow a .\overrightarrow b = 1.( - 1) + ( - 1).1 = - 2 \ne 0\) nên \(\overrightarrow a \) và \(\overrightarrow b \) không vuông góc với nhau.
C. Ta có: \(\overrightarrow z .\overrightarrow t = a.( - b) + b.a = 0\) nên \(\overrightarrow z \) và \(\overrightarrow t \) vuông góc với nhau.
Chọn đáp án C
D. Ta có: \(\overrightarrow n .\overrightarrow k = 1.2 + 1.0 = 2 \ne 0\) nên \(\overrightarrow n \) và \(\overrightarrow k \) không vuông góc với nhau.
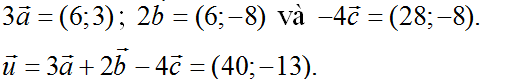
a) Tọa độ của vectơ \(\overrightarrow u + \overrightarrow v + \overrightarrow w \) là: \(\overrightarrow u + \overrightarrow v + \overrightarrow w = \left( { - 2 + 0 + \left( { - 2} \right);0 + 6 + 3} \right) = \left( { - 4;9} \right)\)
b) Ta có: \(\overrightarrow w + \overrightarrow u = \overrightarrow v \Leftrightarrow \overrightarrow w = \overrightarrow v - \overrightarrow u \) nên \(\overrightarrow w = \left( {0 - \sqrt 3 ; - \sqrt 7 - 0} \right) = \left( { - \sqrt 3 ; - \sqrt 7 } \right)\)