Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1)
vì | 1 - 2x | \(\ge\)0 \(\Rightarrow\)| 1 - 2x | - 2009 \(\ge\)-2009
\(\Rightarrow\)GTNN của A là -2009 khi | 1 - 2x | = 0 hay x = \(\frac{1}{2}\)
2)
\(\frac{x}{y}=\frac{2}{5}\Rightarrow\frac{x}{2}=\frac{y}{5}=\frac{x+y}{2+5}=\frac{-21}{7}=-3\)
\(\Rightarrow x=\left(-3\right).2=-6;y=\left(-3\right).5=-15\)
3)
2225 = ( 23 )75 = 875
3150 = ( 32 )75 = 975
vì 875 < 975 nên 2225 < 3150

Bài 1 :
Ta có :
\(A=\frac{\frac{3}{4}-\frac{3}{11}+\frac{3}{13}}{\frac{5}{7}-\frac{5}{11}+\frac{5}{13}}+\frac{\frac{1}{2}-\frac{1}{3}+\frac{1}{4}}{\frac{5}{4}-\frac{5}{6}+\frac{5}{8}}\)
\(A=\frac{3\left(\frac{1}{4}-\frac{1}{11}+\frac{1}{13}\right)}{5\left(\frac{1}{7}-\frac{1}{11}+\frac{1}{13}\right)}+\frac{\frac{1}{2}-\frac{1}{3}+\frac{1}{4}}{\frac{5}{2}\left(\frac{1}{2}-\frac{1}{3}+\frac{1}{4}\right)}\)
\(A=\frac{3}{5}+\frac{1}{\frac{5}{2}}\)
\(A=\frac{3}{5}+\frac{2}{5}\)
\(A=1\)
\(b)\) Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{y+z-x}{x}=\frac{z+x-y}{y}=\frac{x+y-z}{z}=\frac{y+z-x+z+x-y+x+y-z}{x+y+z}=\frac{2\left(x+y+z\right)}{x+y+z}=2\)
Đo đó :
\(\frac{y+z-x}{x}=2\)\(\Rightarrow\)\(y+z=3x\)\(\left(1\right)\)
\(\frac{z+x-y}{y}=2\)\(\Rightarrow\)\(x+z=3y\)\(\left(2\right)\)
\(\frac{x+y-z}{z}=2\)\(\Rightarrow\)\(x+y=3z\)\(\left(3\right)\)
Lại có : \(B=\left(1+\frac{x}{y}\right)\left(1+\frac{y}{z}\right)\left(1+\frac{z}{x}\right)=\frac{x+y}{y}.\frac{y+z}{z}.\frac{x+z}{x}\)
Thay (1), (2) và (3) vào \(B=\frac{x+y}{y}.\frac{y+z}{z}.\frac{x+z}{x}\) ta được :
\(B=\frac{2z}{y}.\frac{2x}{z}.\frac{2y}{x}=\frac{8xyz}{xyz}=8\)
Vậy \(B=8\)
Chúc bạn học tốt ~
bạn phùng minh quân câu 1 a tại sao lại rút gọn được \(\frac{3.\left(\frac{1}{4}-\frac{1}{11}+\frac{1}{13}\right)}{5\left(\frac{1}{7}-\frac{1}{11}+\frac{1}{13}\right)}=\frac{3}{5}\) vậy nó không cùng nhân tử mà
câu b \(\frac{y+z-x+z+x-y+x+y-z}{x+y+z}=\frac{\left(y-y+y\right)+\left(-x+x+x\right)+\left(z+z-z\right)}{x+y+z}=\frac{x+y+z}{x+y+z}=1\)sao lại ra bằng 2
(mình chỉ góp ý thôi nha tại mình làm thấy nó sai sai)

\(x^2=yz\Rightarrow\frac{x}{y}=\frac{z}{x}\left(1\right)\)
\(y^2=xz\Rightarrow\frac{x}{y}=\frac{y}{z}\left(2\right)\)
\(\left(1\right),\left(2\right)\Rightarrow\frac{x}{y}=\frac{y}{z}=\frac{z}{x}=\frac{x+y+z}{y+z+x}=1\)
\(\Rightarrow x=y=z\)
Thay y, z bằng x \(\Rightarrow M=\frac{3.x^{2019}}{\left(3x\right)^{2019}}=\frac{3x^{2019}}{3^{2019}.x^{2019}}=\frac{1}{3^{2018}}\)

thay x= -1/2 ; y= 4; z =6 vào biểu thức A
có: \(A=\left(\frac{-1}{2}\right)^2.4+\left(\left(\frac{-1}{2}\right)^3-3.\frac{-1}{2}.4.6\right)+\left(-14^{15}\right)^0\)
\(A=\frac{1}{4}.4+\left(\frac{-1}{8}-\left(-36\right)\right)+1\)
\(A=1+35\frac{7}{8}+1\)
\(A=37\frac{7}{8}\)
KL: \(A=37\frac{7}{8}\) tại x= -1/2 ; y=4; z=6
CHÚC BN HỌC TỐT!!!
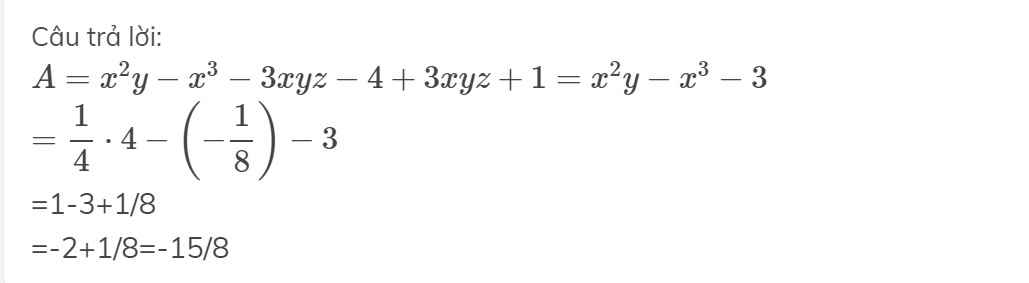
a/ \(M=x^4-xy^3+x^3y-y^4-1\)
\(\Leftrightarrow M=x^3\left(x+y\right)-y^3\left(x+y\right)-1\)
Mà \(x+y=0\)
\(\Leftrightarrow M=x^3.0-y^3.0-1\)
\(\Leftrightarrow M=-1\)
Vậy ...
cau b lam nhu the nao vay