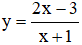Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(f\left(0\right)=\dfrac{b}{d}\Rightarrow f\left(f\left(0\right)\right)=0\Rightarrow f\left(\dfrac{b}{d}\right)=0\)
\(\Rightarrow\dfrac{\dfrac{ab}{d}+b}{\dfrac{cb}{d}+d}=0\Rightarrow b\left(a+d\right)=0\Rightarrow\left[{}\begin{matrix}b=0\\d=-a\end{matrix}\right.\)
TH1: \(b=0\)
\(f\left(1\right)=1\Rightarrow a=c+d\)
\(f\left(2\right)=2\Rightarrow2a=2\left(2c+d\right)\Rightarrow a=2c+d\)
\(\Rightarrow2c+d=c+d\Rightarrow c=0\) (ktm)
TH2: \(d=-a\)
\(f\left(1\right)=1\Rightarrow a+b=c+d=c-a\Rightarrow2a+b=c\) (1)
\(f\left(2\right)=2\Rightarrow2a+b=2\left(2c+d\right)=2\left(2c-a\right)\Rightarrow4a+b=4c\) (2)
Trừ (2) cho (1) \(\Rightarrow2a=3c\Rightarrow\dfrac{a}{c}=\dfrac{3}{2}\)
\(\Rightarrow\lim\limits_{x\rightarrow\infty}\dfrac{ax+b}{cx+d}=\dfrac{a}{c}=\dfrac{3}{2}\)
Hay \(y=\dfrac{3}{2}\) là tiệm cận ngang

Ta có \(f'\left(x\right)=3ax^2+2bx+c;f"\left(x\right)=6ax+2b\)
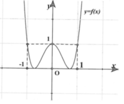
Hàm số \(f\left(x\right)\) đạt cực tiểu tại \(x=0\) khi và chỉ khi
\(\begin{cases}f'\left(0\right)=0\\f"\left(0\right)>0\end{cases}\)\(\Leftrightarrow\begin{cases}c=0\\2b>0\end{cases}\)\(\Leftrightarrow\begin{cases}c=0\\b>0\end{cases}\left(1\right)\)
Hàm số \(f\left(x\right)\) đạt cực đại tại \(x=1\) khi và chỉ khi \(\begin{cases}f'\left(1\right)=0\\f"\left(1\right)< 0\end{cases}\)\(\Leftrightarrow\begin{cases}3a+2b+c=0\\6a+2b< 0\end{cases}\)
\(\begin{cases}f\left(0\right)=0\\f\left(1\right)=1\end{cases}\)\(\Leftrightarrow\begin{cases}d=0\\a+b+c+d=1\end{cases}\) \(\Leftrightarrow\begin{cases}d=0\\a+b+c+d=1\end{cases}\) (3)
Từ (1), (2), (3) suy ra \(a=-2;b=3;c=0;d=0\)
Kiểm tra lại \(f\left(x\right)=-2x^3+3x^2\)
Ta có \(f'\left(x\right)=-6x^2+6x;f"\left(x\right)=-12x+6\)
\(f"\left(0\right)=6>0\), hàm số đạt cực tiểu tại \(x=0\)
\(f"\left(1\right)=-6< 0\), hàm số đạt cực đại tại \(x=1\)
Vậy \(a=-2;b=3;c=0;d=0\)

Lời giải:
\(\frac{3x^3f(x)}{f'(x)^2+xf'(x)+x^2}=f'(x)-x\)
\(\Rightarrow 3x^3f(x)=[f'(x)-x][f'(x)^2+xf'(x)+x^2]=f'(x)^3-x^3\)
\(\Rightarrow 3f(x)=\left(\frac{f'(x)}{x}\right)^3-1\)
Đặt \(\frac{f'(x)}{x}=g(x)\Rightarrow f'(x)=xg(x)(1)\) .
Vì \(f(1)=\frac{7}{3}\Rightarrow f'(1)=2\Rightarrow g(1)=2\)
Ta có: \(3f(x)=g(x)^3-1\)
\(\Rightarrow 3f'(x)=3g'(x)g(x)^2\)
\(\Rightarrow f'(x)=g'(x)g(x)^2(2)\)
Từ \((1);(2)\Rightarrow xg(x)=g'(x)g(x)^2\)
\(\Rightarrow x=g'(x)g(x)=\frac{1}{2}[g(x)^2]'\) \(\Rightarrow 2x=[g(x)^2]'\Rightarrow g(x)^2=\int 2xdx=x^2+c\)
Kết hợp với $g(1)=2$ suy ra $c=3$
Vậy \(g(x)^2=x^2+3\Rightarrow f(x)=\frac{g(x)^3-1}{3}=\frac{(x^2+3)^{\frac{3}{2}}-1}{3}\)
\(\Rightarrow f(2)=\frac{\sqrt{343}-1}{3}\)