
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(1,\dfrac{3x+2}{6}-\dfrac{3x-2}{4}=\dfrac{15}{8}\\ \Leftrightarrow\dfrac{4\left(3x+2\right)}{24}-\dfrac{6\left(3x-2\right)}{24}-\dfrac{45}{24}=0\\ \Leftrightarrow12x+24-18x+12-45=0\\ \Leftrightarrow-6x-9=0\\ \Leftrightarrow x=-\dfrac{3}{2}\)
2, ĐKXĐ:\(x\ne\pm3\)
\(\dfrac{x+2}{3+x}-\dfrac{x}{3-x}=\dfrac{8x-6}{9-x^2}\\ \Leftrightarrow\dfrac{\left(x+2\right)\left(3-x\right)}{\left(3+x\right)\left(3-x\right)}-\dfrac{x\left(3+x\right)}{\left(3+x\right)\left(3-x\right)}-\dfrac{8x-6}{\left(3+x\right)\left(3-x\right)}=0\\ \Leftrightarrow\dfrac{-x^2+x+6-3x-x^2-8x+6}{\left(3+x\right)\left(3-x\right)}=0\\ \Leftrightarrow-2x^2-10x+12=0\\ \Leftrightarrow x^2+5x-6=0\\ \Leftrightarrow\left(x-1\right)\left(x+6\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=1\left(tm\right)\\x=-6\left(tm\right)\end{matrix}\right.\)
\(a,\dfrac{3x+2}{6}-\dfrac{3x-2}{4}=\dfrac{15}{8}\)
\(\Leftrightarrow4\left(3x+2\right)-6\left(3x-2\right)=45\)
\(\Leftrightarrow12x+8-18x+12=45\)
\(\Leftrightarrow12x-18x=45-12-8\)
\(\Leftrightarrow-6x=25\)
\(\Leftrightarrow x=\dfrac{-25}{6}\)
Vậy \(S=\left\{\dfrac{-25}{6}\right\}\)
\(b,\dfrac{x+2}{3+x}-\dfrac{x}{3-x}=\dfrac{8x-6}{9-x^2}\left(ĐKXĐ:x\ne3;x\ne-3\right)\)
\(\Leftrightarrow\left(x+2\right)\left(3-x\right)-x\left(3+x\right)=8x-6\)
\(\Leftrightarrow3x-x^2+6-2x-3x-x^2=8x-6\)
\(\Leftrightarrow-x^2-x^2+3x-2x-3x-8x=-6+6\)
\(\Leftrightarrow-2x^2-10x=0\)
\(\Leftrightarrow-2x\left(x-5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}-2x=0\\x-5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\left(nhận\right)\\x=5\left(nhận\right)\end{matrix}\right.\)
Vậy \(S=\left\{0;5\right\}\)

a) ( x - 3 )3 - ( x - 3 )( x2 + 3x + 9 ) + 9( x + 1 )2 = 4
<=> x3 - 9x2 + 27x - 27 - ( x3 - 27 ) + 9( x2 + 2x + 1 ) = 4
<=> x3 - 9x2 + 27x - 27 - x3 + 27 + 9x2 + 18x + 9 = 4
<=> 45x + 9 = 4
<=> 45x = -5
<=> x = -5/45 = -1/9
b) x( x - 5 )( x + 5 ) - ( x + 2 )( x2 - 2x + 4 ) = 17
<=> x( x2 - 25 ) - ( x3 + 8 ) = 17
<=> x3 - 25x - x3 - 8 = 17
<=> -25x - 8 = 17
<=> -25x = 25
<=> x = -1

a: \(\dfrac{3x+2}{4}-\dfrac{3x+1}{3}=\dfrac{5}{6}\)
=>3(3x+2)-4(3x+1)=10
=>9x+6-12x-4=10
=>-3x+2=10
=>-3x=8
=>x=-8/3
b: \(\dfrac{x-1}{x+2}-\dfrac{x}{x-2}=\dfrac{9x-10}{4-x^2}\)
=>(x-1)(x-2)-x(x+2)=-9x+10
=>x^2-3x+2-x^2-2x=-9x+10
=>-5x+2=-9x+10
=>x=2(loại)

Vì GTTĐ luôn lớn hơn hoặc bằng 0 với mọi x, do đó :
\(\left|x+1\right|+\left|2x+15\right|+\left|3x+6041\right|\ge0\forall x\)
\(\Leftrightarrow7x\ge0\)
\(\Leftrightarrow x\ge0\)
Từ điều kiện này của x ta có phương trình :
\(x+1+2x+15+3x+6041=7x\)
\(\Leftrightarrow6x+6057=7x\)
\(\Leftrightarrow7x-6x=6057\)
\(\Leftrightarrow x=6057\)
Vậy tập nghiệm của pt là S = { 6057 }

\(x^4-3x^3-6x^2+3x+1\)
\(=x^4-2x^2+1-3x^3+3x-4x^2\)
\(=\left(x^2-1\right)^2-3x\left(x^2-1\right)-4x^2\)
đặt \(a=x^2-1\) khi đó biểu thức trở thành
\(a^2-3ax-4x^2\)
\(=a^2+ax-4ax-4x^2\)
\(=\left(a+x\right)\left(a-4x\right)\)
\(=\left(x^2+x-1\right)\left(x^2-4x+1\right)\)

Mình ko ghi lại đề , bạn ghi ra xong rồi suy ra như mình nha .
1) \(=>A=\left(6x^2+3x-10x-5\right)-\left(6x^2+14x-9x-21\right)\)
\(=>A=-12x+16\)
2) \(=>B=8x^3+27-8x^3+2=29\)
3)\(=>C=[\left(x-1\right)-\left(x+1\right)]^3=\left(-2\right)^3=-8\)
4)\(=>D=[\left(2x+5\right)-\left(2x\right)]^3=5^3=125\)
5)\(=>E=\left(3x+1\right)^2-\left(3x+5\right)^2+12x+2\left(6x+3\right)\)
\(=>E=\left(3x+1+3x+5\right)\left(3x+1-3x-5\right)+12x+12x+6\)
\(=>E=\left(6x+6\right)\left(-4\right)+24x+6=-24x-24+24x+6=-18\)
6)\(=>F=\left(2x^2+3x-10x-15\right)-\left(2x^2-6x\right)+x+7=-8\)
k cho mik nha ,

a: =>6x-3x^2-5=4-3x^2-2
=>6x-5=2
=>6x=7
=>x=7/6
b: =>20x+5-12x^2-3x=6x^2-10x+3x-5
=>-12x^2+17x+5-6x^2+7x+5=0
=>-18x^2+24x+10=0
=>x=5/3 hoặc x=-1/3
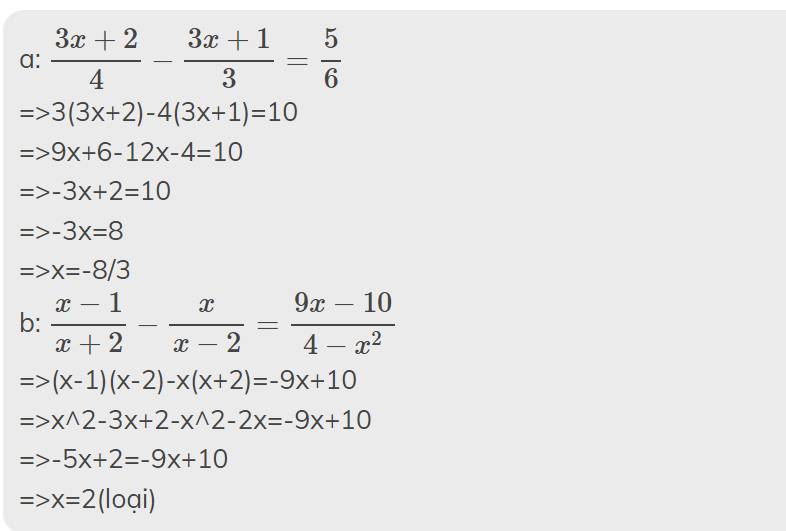
\(\left(3x-4\right)\left(x-2\right)=3x\left(x-9\right)-3\)
\(\Leftrightarrow3x^2-6x-4x+8=3x^2-27x-3\)
\(\Leftrightarrow17x=-11\)
\(\Rightarrow x=\dfrac{-11}{17}\)