Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Trước khi bước lên bậc thang đầu tiên thì thế năng bằng 0
=> Cơ năng: \(W = {W_d} = \frac{1}{2}m{v^2} = \frac{1}{2}.55.1,{5^2} = 61,875(J)\)
b) Khi bước lên bậc thang trên cùng thì động năng bằng 0
=> Cơ năng: \(W = {W_t} = m.g.h = 55.10.3,75 = 2062,5(J)\)
c) Phần năng lượng thay đổi ở hai vị trí do thế năng tăng dần trong khi đó động năng không thay đổi.

a, Ngoại lực tác dụng lên thang máy là trọng lực và kéo của động cơ thang máy. Áp dụng định lý về động năng ta có: Wđ1 – Wđ0 = A F 1 → + A P 1 →
Mà Wđ1 = m . v 1 2 2 , Wđ0 = m . v 0 2 2 = 0 ;
A P 1 → = − P . s 1 = − m . g . s 1 ( A P → 1 < 0 )
Vì thang máy đi lên
⇒ A F 1 = m . v 1 2 2 + m . g . s 1 = 1 2 .1000.5 2 + 1000.10.5 = 62500 J
b, Vì thang máy chuyển động đều, lực kéo của động cơ cân bằng với trọng lực P → : F 2 → + P → = 0 . Công phát động của động cơ có độ lớn bằng công cản A F 2 → = − A P → với A P = − P . s 2 = − m . g . s 2
=> AF2 = mgs2 do đó công suất của động cơ thang máy trên đoạn đường s2 là:
℘ 2 = A F 2 t = m . g . s 2 t = m . g . v 2 = m . g . v 1 ⇒ ℘ 2 = 1000.10.5 = 50000 ( W ) = 50 ( k W ) .
c, Ngoại lực tác dụng lên thang máy là trọng lực P → và lực kéo F 3 → của động cơ.
Áp dụng định lí động năng ta có: Wđ3 – Wđ2 = AF3 + Ap’
Mà Wđ3 = m . v 3 2 2 = 0 ; Wđ2 = m v 2 2 2 (v2 = v1 = 5m/s); Ap = - Ps3 = - mgs3
Công của động cơ trên đoạn đường s3 là: AF3 = mgs3 - m v 2 2 2 = 37500J
Áp dụng công thức tính công ta tìm được lực trung bình do động cơ tác dụng lên thang máy trên đoạn đường s3: F 3 ¯ = A F 3 s 3 = 37500 5 = 7500 N

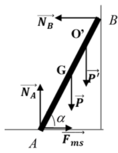
a. Trọng lượng của thanh: P = mg = 200N
Theo điều kiện cân bằng Momen
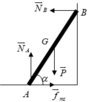
M P → = M N → B ⇒ P . A B 2 cos α = N B . A B . sin α
Theo điều kiện cân bằng lực
P → + N → A + N → B + F → m s = 0 → N A = P = 200 N ; F m s = N B ⇒ N B = F m s = P 2 = 100 N
b, Điều kiện: Fms <k.NA
Theo câu a F m s = N B = P 2 t g α
⇒ N A = P ⇒ t g α > 1 2 k = 1 1 , 2 ⇒ α = 40 0
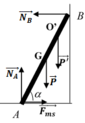
c. Lấy O’ là vị trí người khi thang bắt đầu trượt.
Ta có:
N B = F m s = k N A ; N A = P + P ' = 600 N F m s = 360 N
Xét trục quay qua A
M N → B = M P → + M P ' → N B . A B sin α = P . A B 2 . cos α + P ' . A O ' . cos α ⇒ A O ' = 1 , 3 m


Chọn D.
Lấy O’ là vị trí người khi thang bắt đầu trượt.
Theo điều kiện cân bằng lực:
![]()
→NB = Fms = k.NA; NA = P + P’ = 600 N
Fms = 360N
Xét trục quay qua A:


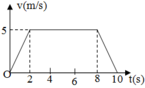
Gia tốc của vật trong từng giai đoạn chuyển động
+ GĐ 1: a 1 = v 2 − v 1 t 1 = 5 − 0 2 = 2 , 5 m / s 2
+ GĐ 2: a 2 = v 3 − v 2 t 2 = 5 − 5 8 = 0 m / s 2
+ GĐ 3: a 3 = v 2 − v 2 t 3 = 0 − 5 2 = − 2 , 5 m / s 2
a. + Giai đoạn 1: Thang máy đi lên nhanh dần đều với gia tốc 2 , 5 m / s 2 ⇒ a → q t ↓ ↓ g → ⇒ g / = g + a q t
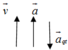
⇒ g / = 10 + 2 , 5 = 12 , 5 m / s 2 ⇒ T = P / = m g / = 1000.12 , 5 = 12500 N
+ Giai đoạn 2: Vì thang máy chuyển động thẳng đều nên a = 0 m / s 2
⇒ T = P = m g = 1000.10 = 10000 N
+ Giai đoạn 3: Đi lên chậm dần đều với gia tốc 2 , 5 m / s 2 ⇒ a → q t ↑ ↓ g → ⇒ g / = g − a q t

⇒ g / = 10 − 2 , 5 = 7 , 5 m / s 2 ⇒ T = P / = m g / = 1000.7 , 5 = 7500 N
b. Thang máy đi xuống
+ Giai đoạn 1: Đi xuống nhanh dần đều với gia tốc 2 , 5 m / s 2 ⇒ a → q t ↑ ↓ g → ⇒ g / = g − a q t
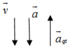
⇒ g / = 10 − 2 , 5 = 7 , 5 m / s 2 ⇒ T = P / = m g / = 1000.7 , 5 = 7500 N
+ Giai đoạn 2: Vì thang máy chuyển động thẳng đều nên a = 0 m / s 2 ⇒ T = P = m g = 1000.10 = 10000 N
+ Giai đoạn 3: Đi xuống chậm dần đều với gia tốc 2 , 5 m / s 2 ⇒ a → q t ↓ ↓ g → ⇒ g / = g + a q t
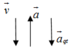
c. Thang máy đi xuống
+ Giai đoạn 1: Đi xuống nhanh dần đều với gia tốc 2 , 5 m / s 2 ⇒ a → q t ↑ ↓ g → ⇒ g / = g − a q t
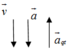
⇒ g / = 10 − 2 , 5 = 7 , 5 m / s 2 ⇒ N = P / = m g / = 80.7 , 5 = 600 N
+ Giai đoạn 2: Vì thang máy chuyển động thẳng đều nên a = 0 m / s 2 ⇒ T = P = m g = 80.10 = 800 N
+ Giai đoạn 3: Đi xuống chậm dần đều với gia tốc 2 , 5 m / s 2 ⇒ a → q t ↓ ↓ g → ⇒ g / = g + a q t
⇒ g / = 10 + 2 , 5 = 12 , 5 m / s 2 ⇒ N = P / = m g / = 80.12 , 5 = 1000 N
Để trọng lượng của ngừơi bằng 0 khi
P / = 0 ⇒ g / = 0 ⇒ a → q t ↑ ↓ g → a q t = g
Tức là lúc này thang máy rơi tự do.