Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Nhận định: Một vật nếu không chịu tác dụng của lực nào (vật tự do) thì vật đó giữ nguyên trạng thái đứng yên hoặc chuyển động thẳng đều mãi mãi.
- Giải thích: Các vật tự do trên thực tế có thể là các vật đứng yên trên mặt phẳng nằm ngang hay các vệ tinh nhân tạo chuyển động đều quanh Trái Đất, … Sở dĩ các vật tự do đó tồn tại được là vì không chịu tác dụng của lực nào hoặc chịu tác dụng của các lực nhưng tổng hợp lực bằng không.

Trên thực tế, không tồn tại hệ kín lí tưởng. Vì môi trường luôn luôn có sự tương tác vật chất với nhau.

Trên thực tế, không tồn tại hệ kín lí tưởng. Vì môi trường luôn luôn có sự tương tác vật chất với nhau.

- Vận dụng kiến thức về sự rơi tự do để tính toán được thời gian rơi của vật, vận tốc vật bắt đầu chạm đất hoặc có thể tìm được độ cao của vật khi được thả rơi tự do.
- Biết cách xác định phương thẳng đứng và phương ngang dựa vào cách sử dụng dây dọi và thước eke.

Tóm tắt:
\(h=25m\)
\(W_t=\frac{1}{2}.W_đ\Rightarrow2.W_t=W_đ\)
_________________________
\(v_{cđ}=?m/s\)
\(v=?m/s\)
Giải:
a) Vận tốc khi chạm đất:
\(v_{cđ}=\sqrt{2.h.g}=\sqrt{2.25.10}=10\sqrt{5}\simeq22,36\left(m/s\right)\)
b) Thế năng tại C:
\(W_C=W_{đ_C}+W_{t_C}=3W_{t_C}\)
Bảo toàn cơ năng: \(W_A=W_C\)
\(\Leftrightarrow250.m=3.m.g.h_C\)
\(\Leftrightarrow h_C=\frac{25}{3}\left(m\right)\)
\(\Rightarrow t=\frac{5}{3}\left(s\right)\)
\(\Rightarrow v=t.g=\frac{5}{3}.10=\frac{50}{3}\simeq16,67\left(m/s\right)\)
Vậy ... ( kết quả khác nhưng gần bằng ? )
Chúc bạn học tốt

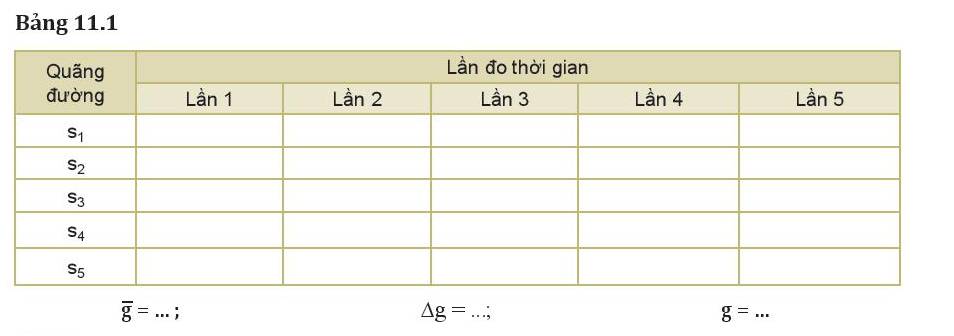
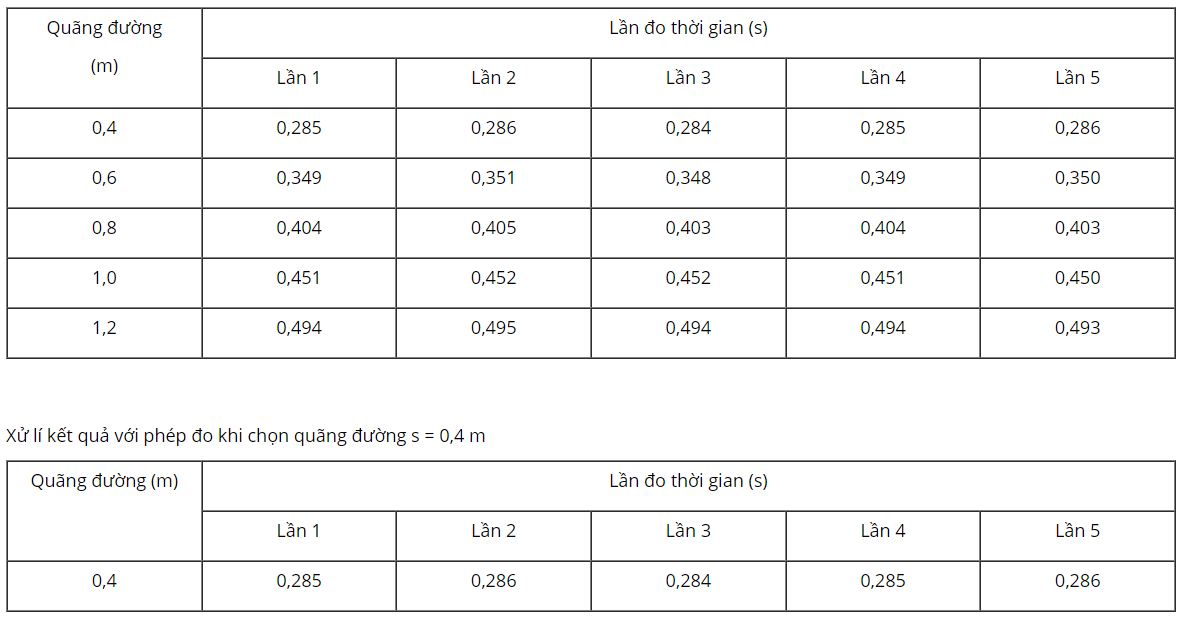
1. Tính giá trị trung bình và sai số tuyệt đối của phép đo gia tốc rơi tự do
- Lần 1: \({g_1} = \frac{{2{s_1}}}{{t_1^2}} = \frac{{2.0,4}}{{0,{{285}^2}}} = 9,849(m/{s^2})\)
- Lần 2: \({g_2} = \frac{{2{s_2}}}{{t_2^2}} = \frac{{2.0,4}}{{0,{{285}^2}}} = 9,849(m/{s^2})\)
- Lần 3: \({g_3} = \frac{{2{s_3}}}{{t_3^2}} = \frac{{2.0,4}}{{0,{{285}^2}}} = 9,919(m/{s^2})\)
- Lần 4: \({g_4} = \frac{{2{s_4}}}{{t_4^2}} = \frac{{2.0,4}}{{0,{{285}^2}}} = 9,849(m/{s^2})\)
- Lần 5: \({g_5} = \frac{{2{s_5}}}{{t_5^2}} = \frac{{2.0,4}}{{0,{{286}^2}}} = 9,780(m/{s^2})\)
Gia tốc trung bình là: \(\overline g = \frac{{9,849 + 9,849 + 9,919 + 9,849 + 9,780}}{5} = 9,849(m/{s^2})\)
Sai số tuyệt đối của gia tốc trong các lần đo
\(\begin{array}{l}\Delta {g_1} = \left| {\overline g - {g_1}} \right| = \left| {9,849 - 9,849} \right| = 0\\\Delta {g_2} = \left| {\overline g - {g_2}} \right| = \left| {9,849 - 9,849} \right| = 0\\\Delta {g_3} = \left| {\overline g - {g_3}} \right| = \left| {9,849 - 9,919} \right| = 0,07\\\Delta {g_4} = \left| {\overline g - {g_4}} \right| = \left| {9,849 - 9,849} \right| = 0\\\Delta {g_5} = \left| {\overline g - {g_5}} \right| = \left| {9,849 - 9,780} \right| = 0,069\end{array}\)
Sai số tuyệt đối trung bình là: \(\overline {\Delta g} = \frac{{\Delta {g_1} + \Delta {g_2} + \Delta {g_3} + \Delta {g_4} + \Delta {g_5}}}{5} = 0,028\)
Suy ra kết quả: \(g = 9,849 \pm 0,028\)
2. Trong thí nghiệm người ta dùng trụ thép làm vật rơi nhằm mục đích khi ta thả vật rơi thì xác suất phương rơi của vật chắn tia hồng ngoại ở cổng quang điện cao, giúp ta thực hiện thí nghiệm dễ dàng hơn
- Có thể dùng vật thả rơi là viên bi thép, nhưng xác suất khi thả rơi viên bi có phương rơi không chắn được tia hồng ngoại cao hơn khi dùng trụ thép, nên khi làm thí nghiệm với viên bi ta cần căn chỉnh và thả theo đúng phương của dây rọi.

a. Tại vị trí thả vật, động năng của vật bằng 0, thế năng của vật cực đại
\(W_{tmax}=mgh_{max}=1000\) J
b. Áp dụng ĐLBT cơ năng cho vật tại ví trí thả và mặt đất có
\(W_{tmax}=W_{đmax}\)
\(\Rightarrow\frac{1}{2}mv_{max}^2=1000\)
\(\Rightarrow v_{max}=31,6\) m/s
c. Tại vị trí động năng bằng thế năng có
\(W=W_t+W_đ=2W_t\)
\(\Rightarrow W_{tmax}=2W_t\Rightarrow h=\frac{h_{max}}{2}=25\) m
d. Vận tốc của vật tại vị trí đó là
\(\frac{1}{2}mv^2=mgh\Rightarrow v=\sqrt{2gh}=22,4\) m/s
Nhận định: Một vật nếu không chịu tác dụng của lực nào (vật tự do) thì vật đó giữ nguyên trạng thái đứng yên, hoặc chuyển động thẳng đều mãi mãi.