Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giả sử điện tích trong hai mạch dao động biến đổi theo quy luật
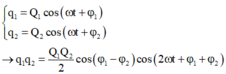
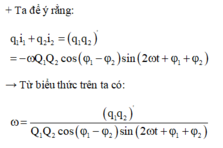
Tần số góc nhỏ nhất khi mẫu số là lớn nhất, các hàm lượng giác cực đại bằng 1
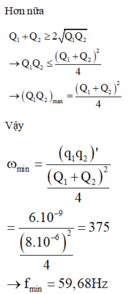
Đáp án D

Giải:
Cho \(q_1=10^{-9}C\) và \(i_1=6mA\) và \(4q_1^2+q^2_2=1,3.10^{-17}\left(1\right)\)
Thay \(q_1=10^{-9}C\) vào \(\left(1\right)\) ta có:
\(4q^2_1+q_2^2=1,3.10^{-17}\left(1\right)\Rightarrow q_2=3.10^{-9}C\)
\(4q_1^2+q^2_2=1,3.10^{-17}\) lấy đạo hàm 2 vế theo thời gian \(t\)
\(\Rightarrow8q_1i_1+2q_2i_2=0\left(2\right)\)
Thay \(q_1=10^{-9}C\) và \(i_1=6mA\) và \(q_2=3.10^{-9}C\) vào \(\left(2\right)\) ta có:
\(8q_1i_1+2q_2i_2=0\Rightarrow i_2=8mA\)
Vậy ta chọn \(C.\)
Chú ý: dòng điện tức thời \(i = \frac{dq(t)}{dt} = q(t)'\)
\(4q_1(t)^2+q_2(t)^2 = 1,3.10^{-17} .(1)\)
Lấy đạo hàm 2 vễ phương trình (1). Chú ý \((q(t)^n)' = n.q(t)^{n-1}.q(t)'\)
=> \(4.2.q_1(t).q_1(t)' + 2.q_2(t).q_2(t)' = 0\)
=> \(8q_1.i_1 + 2q_2i_2 = 0.(2)\)
Tại thời điểm t có \(q_1 = 10^{-9}C\) . Thay vào \((1)\) => \(q_2 =\sqrt{ 1,3.10^{-17} - 4.10^{-18}} = 3.10^{-9} C.\)
Thay \(q_1 = 10^{-9}C;i_1 = 6mA; q_2 = 3.10^{-9}C \) vào \((2)\) ta được \(i_2 = -8mA.\)
=> Cường độ dòng thứ hai là 8mA. (độ lớn)
Chọn đáp án. C. 8mA
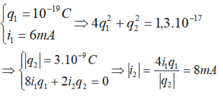
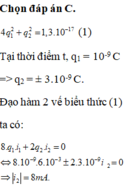




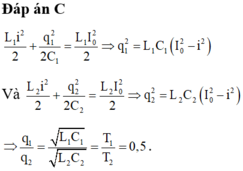
Bài này đã có người hỏi rồi.
Câu trả lời ở đây bạn nhé