Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án cần chọn là: D
Gọi d là khoảng cách từ vật đến thấu kính
d 1 ' là khoảng cách từ ảnh của vật qua thấu kính hội tụ đến thấu kính
d 2 ' là khoảng cách từ ảnh của vật qua thấu kính phân kì đến thấu kính
Ta có:
+ Khi dùng thấu kính hội tụ: 1 f = 1 d + 1 d 1 ' ⇔ 1 f = 1 d + 1 60 (1)
+ Khi dùng thấu kính phân kì: 1 − f = 1 d + 1 d 2 ' ⇔ 1 − f = 1 d + 1 − 12 (2)
Lấy (1) – (2) ta được:
2 f = 1 60 + 1 12 ⇒ f = 20 c m

Đáp án D
Khi d > f, vật ngoài đoạn OI
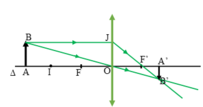
Ảnh là thật, ngược chiều, nhỏ hơn vật

Đáp án: D
Khi d > f, vật ngoài đoạn OI (hình vẽ).
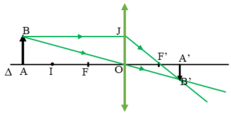
Ảnh là thật, ngược chiều, nhỏ hơn vật.

Đáp án: A
Khi f < d < 2f, vật ở trong đoạn FI (hình vẽ)
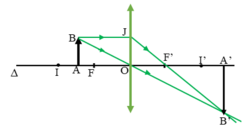
Ảnh thật, ngược chiều, lớn hơn vật và nằm ngoài khoảng OI’.

Đáp án A
Khi f < d < 2f, vật ở trong đoạn FI
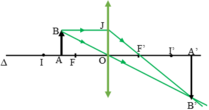
Ảnh thật, ngược chiều, lớn hơn vật và nằm ngoài khoảng OI’

Chọn D
Hướng dẫn:
- Tiêu cự của thấu kính là f = 1 D = 0,2 (m) = 20 (cm).
- Áp dụng công thức thấu kính 1 f = 1 d + 1 d ' với d = 10 (cm) ta tính được d’ = -20 (cm) <0 suy ra ảnh A’B’ là ảnh ảo, nằm trước thấu kính.

3/ \(n\sin i=\sin60^0;\) \(i=90-r\Rightarrow i=30^0\)
\(\Rightarrow n=\dfrac{\sin60^0}{\sin30^0}=\sqrt{3}\)
5/ \(D=\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Leftrightarrow2=\dfrac{1}{0,25}+\dfrac{1}{d'}\Rightarrow d'=-50\left(cm\right)\)
\(k=-\dfrac{d'}{d}=\dfrac{50}{25}=2\)
=>D. Anh ao, cach thau kinh 50cm, k=2
7/ \(d=\dfrac{d'f}{d'-f}\Rightarrow d+d'=d'+\dfrac{d'f}{d'-f}=\dfrac{d'^2-d'f+d'f}{d'-f}=\dfrac{d'^2}{d'-f}\)
\(\left(d+d'\right)_{min}\Leftrightarrow(\dfrac{1}{d'}-\dfrac{f}{d'^2})_{max}\)
Dat \(\dfrac{1}{d'}=a\Rightarrow a-a^2f=-\left(a^2f+a+\dfrac{1}{4f}\right)+\dfrac{1}{4f}=-\left(a\sqrt{f}+\dfrac{1}{2\sqrt{f}}\right)^2\le\dfrac{1}{4f}\)
\("="\Leftrightarrow a\sqrt{f}=\dfrac{1}{2\sqrt{f}}\Leftrightarrow2af=1\Rightarrow a=\dfrac{1}{2f}\)
\(\Rightarrow\dfrac{1}{d'}=\dfrac{1}{2f}\Rightarrow d'=2f\Rightarrow d=\dfrac{d'f}{d'-f}=\dfrac{2f^2}{2f-f}=2f\)
\(\Rightarrow\left(d+d'\right)_{min}=2f+2f=4f\Rightarrow D.4f\)
8/ \(D=\dfrac{1}{f}=-\dfrac{1}{20}=-0,05\left(dp\right)\Rightarrow C.-0,05dp\)
15/ \(k_1=\dfrac{f}{f-d_1};k_2=\dfrac{f}{f-d_2};\dfrac{k_1}{k_2}=-1\)
\(d_2=d_1-12\Rightarrow\dfrac{k_1}{k_2}=-1=\dfrac{f-d_2}{f-d_1}=\dfrac{f-d_1-12}{f-d_1}\) (1)
\(\dfrac{1}{f}=\dfrac{1}{d_1}+\dfrac{1}{d_1'};-\dfrac{d'_1}{d_1}=3\Rightarrow\dfrac{1}{f}=\dfrac{1}{d_1}-\dfrac{1}{3d_1}\)
\(\Rightarrow\dfrac{1}{f}=\dfrac{2}{3d_1}\Rightarrow d_1=\dfrac{2}{3}f\)
Thay vo (1)\(\Rightarrow\dfrac{f-\dfrac{2}{3}f-12}{f-\dfrac{2}{3}f}=-1\Leftrightarrow\dfrac{1}{3}f-12=-\dfrac{1}{3}f\Rightarrow f=18\left(cm\right)\)
19/ \(\sin i=n\sin r=n\cos i\Rightarrow\tan i=n\Rightarrow A.\tan i=n\)
22/ \(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Leftrightarrow\dfrac{1}{20}=\dfrac{1}{d}+\dfrac{1}{d'}\)
\(-d'-d=45\Rightarrow d'=-d-45\Rightarrow\dfrac{1}{20}=\dfrac{1}{d}-\dfrac{1}{d+45}\)
\(\Leftrightarrow d^2+45d=45.20\Leftrightarrow\left[{}\begin{matrix}d=15\left(cm\right)\\d=-60\left(loai\right)\end{matrix}\right.\Rightarrow d'=-60\left(cm\right)\)
2/ \(-\dfrac{d'}{d}=\dfrac{1}{2}\Rightarrow d'=-\dfrac{d}{2}=-30\left(cm\right)\)
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}=\dfrac{1}{60}-\dfrac{1}{30}\Rightarrow D=\dfrac{1}{f}=-\dfrac{1}{60}\left(dp\right)\Rightarrow B\)
8/ C. Tu 0 den f
10/ A.cap uang
12/ \(n_A\sin i=n_B\sin r\Rightarrow\dfrac{n_A}{n_B}=\dfrac{\sin r}{\sin i}=\dfrac{\sin10}{\sin15}\)
\(n_A.\sin30^0=n_B\sin r'\Rightarrow\sin r'=\dfrac{n_A}{n_B}.\sin30^0=\dfrac{\sin10}{\sin15}.\sin30\Rightarrow r'\approx19,6^0\Rightarrow C.19,60\)
17/ \(B=2\pi.10^{-7}.N\dfrac{I}{r}\Rightarrow\) D. Duong kinh vong day tang
20/ \(L_1=4\pi.10^{-7}.\dfrac{N_1^2}{l_1}S;L_2=4\pi.10^{-7}.\dfrac{N_2^2}{l_2}S\)
\(N_1=2N_2;l_1=2l_2\Rightarrow\dfrac{L_1}{L_2}=\dfrac{\dfrac{\left(2N_2\right)^2}{2l_2}}{\dfrac{N_2^2}{l_2}}=2\Rightarrow C.2\)