
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn A
+ Hàm số trùng phương luôn đạt cực trị tại x = 0.
Do đó: x 1 , x 2 , x 3 = 0

a) TXĐ: R
y′ = 6x − 24 x 2 = 6x(1 − 4x)
y' = 0 ⇔ 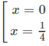
y' > 0 trên khoảng (0; 1/4) , suy ra y đồng biến trên khoảng (0; 1/4)
y' < 0 trên các khoảng ( - ∞ ; 0 ); (14; + ∞ ), suy ra y nghịch biến trên các khoảng ( - ∞ ;0 ); (14; + ∞ )
b) TXĐ: R
y′ = 16 + 4x − 16 x 2 − 4 x 3 = −4(x + 4)( x 2 − 1)
y' = 0 ⇔ 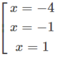
Bảng biến thiên:
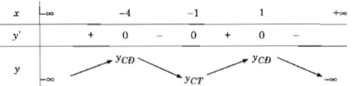
Vậy hàm số y đã cho đồng biến trên các khoảng ( - ∞ ; -4) và (-1; 1), nghịch biến trên các khoảng (-4; -1) và (1; + ∞ )
c) TXĐ: R
y′ = 3 x 2 − 12x + 9
y' = 0
y' > 0 trên các khoảng ( - ∞ ; 1), (3; + ∞ ) nên y đồng biến trên các khoảng ( - ∞ ; 1), (3; + ∞ )
y'< 0 trên khoảng (1; 3) nên y nghịch biến trên khoảng (1; 3)
d) TXĐ: R
y′ = 4 x 3 + 16 = 4x( x 2 + 4)
y' = 0 ⇔ 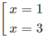
y' > 0 trên khoảng (0; + ∞ ) ⇒ y đồng biến trên khoảng (0; + ∞ )
y' < 0 trên khoảng ( - ∞ ; 0) ⇒ y nghịch biến trên khoảng ( - ∞ ; 0)

Chọn A.
+Cách trắc nghiệm: Có a,b = -4 < 0. Nên hàm số có 3 điểm cực trị x1 = 0, x2, x3 là 2 số đối nhau.
Suy ra x1 + x2 + x3 = 0
+Cách tự luận
![]()


Suy ra x1 + x2 + x3 = 0.

Chọn A.
+Cách trắc nghiệm: Có a,b = -4 < 0. Nên hàm số có 3 điểm cực trị x1 = 0, x2, x3 là 2 số đối nhau.
Suy ra x1 + x2 + x3 = 0
+Cách tự luận
![]()
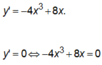

Suy ra x1 + x2 + x3 = 0.
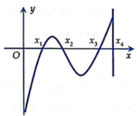

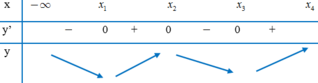

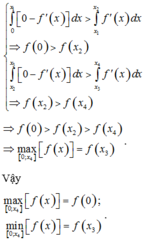

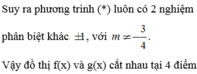
ko ghi nổi số này
~hok tốt~
k nha cảm ơn