Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chu kì dao động: \(T=\dfrac{2\pi}{\omega}=\dfrac{2\pi}{4\pi}=0,5s\)
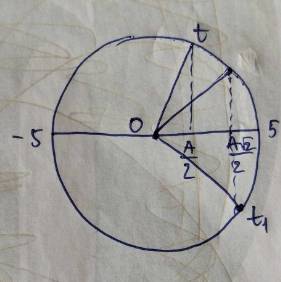
Ta có: \(x=2,5\sqrt{2}=\dfrac{A\sqrt{2}}{2}\) và đang có xu hướng giảm.
Lúc này vật ở thời điểm: \(t_1=\dfrac{T}{8}\)
Tại thời điểm: \(t=\dfrac{7}{48}s=\dfrac{7T}{14}=\dfrac{T}{8}+\dfrac{T}{6}\)
Dựa vào vòng tròn lượng giác \(\Rightarrow x=2,5cm\)

\(A^2=A_1^2+A^2_2+2A_1A_1\cos\left(\widehat{A_1A_1}\right)\Rightarrow\left(\widehat{A_1A_2}\right)=\dfrac{\pi}{2}\)
Chỗ này đề bài ko cho rõ thì chia làm 2 trường hợp, x1 nhanh pha hơn hoặc x2 nhanh pha hơn, rồi tính được phi 2
Bấm máy là xong luôn pha ban đầu của dao động tổng hợp, biết bấm ko để tui chỉ luôn?
Thôi chỉ luôn đi, mất công hỏi nhiều mệt người
SHIFT Mode , cái nút tròn ở giữa ấy, ấn phía bên dưới, rồi nhấn 3, rồi nhấn tiếp 2
Nhấn tiếp Mode, rồi nhấn số 2
Nhấn SHIFT Mode lần nữa, rồi nhấn số 4 để nó chuyển về radian
Nhập theo mẫu sau: A1 SHIFT (-) phi 1 +A2 SHIFT (-) phi 2 , rồi nhất "=",nó sẽ ra kết ủa y hệt cái phương trình đã cho, từ đó tìm được pha ban đầu của phương trình tổng hợp. Biết phi 2, biết phi, dễ dàng tính được biểu thức

Bạn ấn vào biểu tượng fx để nhập công thức nhé, nhìn thế này khó luận lắm.
Một vật khối lượng 300g thực hiện đồng thời hai dao động là x1= \(5\sqrt{3}\) cos(5\(\pi\) t) cm ; x2= 5 cos (5\(\pi\) t -\(\alpha\)) cm. Biết phương trình dao động tổng hợp của vật x= A cos (5\(\pi\)t - \(\beta\)) cm. Biết 0<\(\beta\)<\(\alpha\)<\(\pi\), \(\alpha\)+\(\beta\)=\(\pi\)/2 . Năng lượng dao động của vật là
Giúp mình với nha.Mình đang cần gấp. Cảm ơn trước nhé.

Độ lệch pha của 2 dao động:
\(\Delta \varphi = \dfrac{\pi}{2}\)
Vì 2 dao động vuông pha, nên biên độ dao động tổng hợp:
\(A=\sqrt{A_1^2+A_2^2}=\sqrt{6^2+8^2}=10\) (cm)

Phương trình tổng quát: \(x = A\cos(\omega t +\varphi)\)
+ Quãng đường khi vật thực hiện 5 dao động: S = 5.4A = 100 cm \(\Rightarrow\) A = 5cm.
+ Tần số: f = 5/2 = 2,5 Hz \(\Rightarrow \omega = 2\pi f = 2\pi.2,5 = 5\pi \ (rad/s)\)
+ t= 0 khi vật có x0=5 nên vật đang ở biên độ dương \(\Rightarrow \varphi = 0\)
Vậy phương trình dao động: \(x=5\cos(5\pi t) \ (cm)\)

ta có
x1=\(10\sin\left(20\pi t-\frac{\pi}{4}\right)=10cos\left(20\pi t+\frac{\pi}{4}\right)\)
giải theo máy tính:
- chuyển máy tính sang tính toán số phức:
bấm mode 2.
*Tính dao động thành phần thứ 2:
thao tác:
- bấm \(10\sqrt{2}shift\left(-\right)\frac{-\pi}{4}-10shift\left(-\right)\frac{\pi}{4}\)
=> kết quả - bấm shift 23
=> phương trình của dao động thành phần thứ 2
Máy Fx-570MS
Bước chuẩn bị nhập số liệu vào máy. Chuyển chế độ dùng số phức:
Bấm Mode chọn 2. CMPLX
Ở đây ta sử dụng số đo góc là độ(D), để dùng rad(Chuyển về R).
Nhập: ‘A1’ + ‘Shift’ + ‘(-)’ + ‘φ1’ + ‘+’ + ‘A2’ + ‘Shift’ + ‘(-)’ + ‘φ2’
Bước lấy kết quả. Sau khi nhập biểu thức cộng ‘+’hoặc trừ ‘-’ vectơ.
Nhấn: ‘=’
- Để lấy A (Véctơ kết quả):
Nhấn: ‘Shift’ + ‘+’ + ‘=’
- Để lấy φ (góc hợp bởi vectơ kết quả và vectơ chọn làm gốc):
Nhấn: ‘Shift’ + ‘=’
Với máy Fx-570ES thì để lấy kết quả, chúng ta Nhấn ‘Shift’ + ‘2’ + ‘3’ +‘=’
Chú ý:
- Với các bài toán có dạng đặc biệt chúng ta nên suy luận để lấy kết quả thì nhanh hơn bấm máy.
- Với bài toán cho x1 (hoặc x2) và x, yêu cầu tìm x2 (hoặc x1) thì nhập:
‘A’ + ‘Shift’ + ‘(-)’ + ‘φ’ + ‘-’ + ‘A1(2)’ + ‘Shift’ + ‘(-)’ + ‘φ1(2)’

Phương trình tổng quát: \(x= A cos(\omega t+\varphi)\)
+ Tần số góc: \(\omega = 2\pi/2 = \pi \ (rad/s)\)
+ t=0, vật qua VTCB theo chiều đương \(\Rightarrow\left\{ \begin{array}{} x_0 = 0\ cm\\ v_0 >0 \end{array} \right.\)\(\Rightarrow\left\{ \begin{array}{} \cos \varphi = 0\ cm\\ \sin \varphi <0 \end{array} \right. \Rightarrow \varphi = -\frac{\pi}{2}\)
Vậy phương trình dao động: \(x = 5\cos(\pi t - \frac{\pi}{2})\) (cm)
tại sao lại ra φ=\(\dfrac{-\pi}{2}\) làm cách nào vậy bạn???