Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABC có
BD,CE là đường cao
BD cắt CE tại H
=>H là trực tâm
=>AH vuông góc BC
b: Xét tứ giác BHCK có
BH//CK
BK//CH
=>BHCK là hình bình hành

a: Xét ΔABC có
BE là đường cao
CF là đường cao
BE cắt CF tại H
Do đó: H là trực tâm của ΔBAC
Suy ra: AH\(\perp\)BC
Xét tứ giác BHCD có
BH//CD
CH//BD
Do đó: BHCD là hình bình hành
b: Ta có: BHCD là hình bình hành
nên Hai đường chéo BC và HD cắt nhau tại trung điểm của mỗi đường
mà M là trung điểm của BC
nên M là trung điểm của HD
hay M,H,D thẳng hàng
Ta có: ΔEBC vuông tại E
mà EM là đường trung tuyến
nên EM=BC/2(1)
Ta có: ΔFBC vuông tại F
mà FM là đường trung tuyến
nên FM=BC/2(2)
Từ (1) và (2) suy ra ME=MF
hay ΔEMF cân tại M

a,Xét tam giác ACE và tam giác ABD có:
A chung
AEC=ADB(=90)
→ACE∼ABD(g−g)
b,ACE∼ABD
→AC/AB=AE/AD
→AD/AB=AE/AC
Xét tam giác ADE và tam giác ABC có:
A chung
AD/AB=AE/AC
→ADE∼ABC(c−g−c)
→AED=ACB
Ta có: DEH=90−AED
HBC=90−DCB
→DEH=HBC (Vì AED=DCB-cmt)
Xét tam giác EHD và tam giác HBC có:
EHD=BHC
DEH=HBC
→EDH∼BCH(g−g)
→HE/HB=HD/HC
hay HE.HC=HB.HD

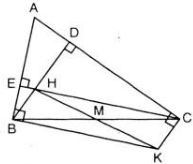
Ta có: CE ⊥ AB (gt)
KB ⊥ AB (gt)
⇒ BK // CE (1)
Tương tự BH // KC (2)
Từ (1) và (2) ⇒ BHCK là hình bình hành.
Gọi M là giao điểm của hai đường chéo BC và HK.
a) Tam giác ABC có hai đường cao BD và CE cắt nhau tại H nên H là trực tâm tam giác ABC
⇒ AH ⊥ BC. (3)
BHCK là hình thoi
⇔ HM ⊥ BC ( trong đó M là giao điểm của hai đường chéo HK và BC) (4)
Từ (3) và (4) suy ra: A, H, M thẳng hàng.
Khi đó,tam giác ABC có AM là đường cao đồng thời là đường trung tuyến nên tam giác ABC là cân tại A.
b) BHCK là hình chữ nhật
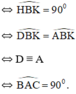
Vậy BHCK là hình chữ nhật khi tam giác ABC vuông tại A.

Bài 1)
Vì HC \(\perp\)AB
DB \(\perp\)AB
=> HC // DB (1) ( Từ vuông góc đến song song)
Vì HB \(\perp\)AC
DC\(\perp\)AC
=> HB//DC(2) ( Từ vuông góc đến song song)
Từ (1) và (2) => BHCD là hình bình hành