Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\Rightarrow\left\{{}\begin{matrix}a=bk\\c=dk\end{matrix}\right.\) (1)
a) Từ (1) ta có:
\(\dfrac{a}{a+b}=\dfrac{bk}{bk+b}=\dfrac{bk}{b\left(k+1\right)}=\dfrac{k}{k+1}\) (2)
\(\dfrac{c}{c+d}=\dfrac{dk}{dk+d}=\dfrac{dk}{d\left(k+1\right)}=\dfrac{k}{k+1}\) (3)
Từ (2) và (3) suy ra \(\dfrac{a}{a+b}=\dfrac{c}{c+d}\)
b) Từ (1) ta có:
\(\dfrac{a^{2018}+c^{2018}}{b^{2018}+d^{2018}}=\dfrac{b^{2018}.k^{2018}+d^{2018}.k^{2018}}{b^{2018}+d^{2018}}=\dfrac{k^{2018}\left(b^{2018}+d^{2018}\right)}{b^{2018}+d^{2018}}=k^{2018}\) (4)
\(\dfrac{\left(a+c\right)^{2018}}{\left(b+d\right)^{2018}}=\dfrac{\left(bk+dk\right)^{2018}}{\left(b+d\right)^{2018}}=\dfrac{\left[k\left(b+d\right)\right]^{2018}}{\left(b+d\right)^{2018}}=k^{2018}\) (5)
Từ (4) và (5) suy ra \(\dfrac{a^{2018}+c^{2018}}{b^{2018}+d^{2018}}=\dfrac{\left(a+c\right)^{2018}}{\left(b+d\right)^{2018}}\)

Bài 1:
2)
Ta có:
\(\frac{x}{4}=\frac{y}{6}\) và \(x+y=5.\)
Áp dụng tính chất dãy tỉ số bằng nhau ta được:
\(\frac{x}{4}=\frac{y}{6}=\frac{x+y}{4+6}=\frac{5}{10}=\frac{1}{2}.\)
\(\Rightarrow\left\{{}\begin{matrix}\frac{x}{4}=\frac{1}{2}\Rightarrow x=\frac{1}{2}.4=2\\\frac{y}{6}=\frac{1}{2}\Rightarrow y=\frac{1}{2}.6=3\end{matrix}\right.\)
Lại có \(A=\left(x-y\right)^{2017}\)
\(\Rightarrow A=\left(2-3\right)^{2017}\)
\(\Rightarrow A=\left(-1\right)^{2017}\)
\(\Rightarrow A=-1.\)
Vậy \(A=-1.\)
Chúc bạn học tốt!

a) \(\dfrac{2a+3c}{2b+3d}\) = \(\dfrac{2a-3c}{2b-3d}\)
Từ \(\dfrac{a}{b}\) = \(\dfrac{c}{d}\) = k ( k \(\in\) Q, k \(\ne\) 0 )
=> \(\left\{{}\begin{matrix}a=bk\\c=dk\end{matrix}\right.\)
VP = \(\dfrac{2a+3c}{2b+3d}\) = \(\dfrac{2.b.k+3.d.k}{2b+3d}\) = \(\dfrac{k.\left(2b+3d\right)}{2b+3d}\) = k (1)
VT = \(\dfrac{2a-3c}{2b-3d}\) = \(\dfrac{2.b.k-3.d.k}{2b-3d}\) = \(\dfrac{k.\left(2b-3d\right)}{2b-3d}\) = k (2)
Từ (1) và (2) ta có: \(\dfrac{2a+3c}{2b+3d}\) = \(\dfrac{2a-3c}{2b-3d}\)
hay: (2a+3c).(3b-3d) = (2a-3c).(2b+3d)

2:
a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
góc ABD=góc EBD
=>ΔBAD=ΔBED
b: Xét ΔDAK vuông tại A và ΔDEC vuông tại E có
DA=DE
góc ADK=góc EDC
=>ΔDAK=ΔDEC
=>DK=DC
=>ΔDKC cân tại D

a) Ta có: ΔDBC vuông tại D(BD⊥AC tại D)
mà DO là đường trung tuyến ứng với cạnh huyền BC(O là trung điểm của BC)
nên \(DO=\dfrac{BC}{2}\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)
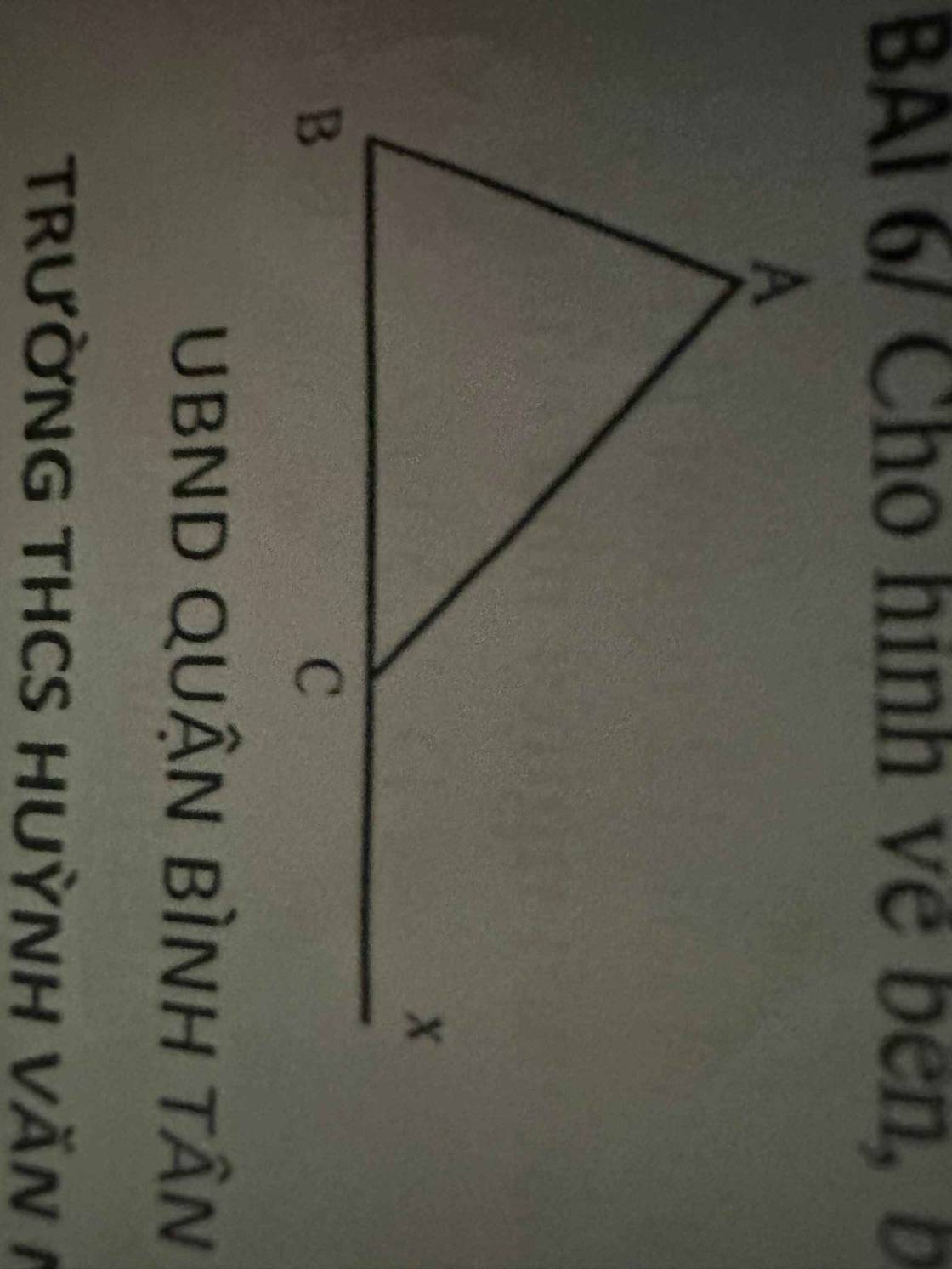
Giảng cho e vs ak e cần gấp

