Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Chọn mp(ABCD) có chứa CD
Xét ΔSBD có
E,I lần lượt là trung điểm của SB,SD
=>EI là đường trung bình của ΔSBD
=>EI//BD
Xét (ABCD) và (AIE) có
\(A\in\left(ABCD\right)\cap\left(AIE\right)\)
EI//BD
Do đó: (ABCD) giao (AIE)=xy, xy đi qua A và xy//BD//EI
Gọi K là giao điểm của xy với CD
=>K là giao điểm của CD với mp(AIE)
a: Chọn mp(ABCD) có chứa CD
Xét ΔSBD có
E,I lần lượt là trung điểm của SB,SD
=>EI là đường trung bình của ΔSBD
=>EI//BD
Xét (ABCD) và (AIE) có
EI//BD
Do đó: (ABCD) giao (AIE)=xy, xy đi qua A và xy//BD//EI
Gọi K là giao điểm của xy với CD
=>K là giao điểm của CD với mp(AIE)

Kéo dài AD và BC cắt nhau tại E
\(\Rightarrow SE=\left(SAD\right)\cap\left(SBC\right)\)
Trong mp (SBC), nối MN kéo dài cắt SE tại F
Trong mp (SAD), nối AF cắt SD tại I
\(\Rightarrow I=SD\cap\left(AMN\right)\)
Tứ giác AINM chính là thiết diện của (AMN) và chóp
MN là đường trung bình tam giác SCD \(\Rightarrow F\) là trung điểm SE
Mặt khác CD song song và bằng 1/2 AB \(\Rightarrow\) CD là đường trung bình tam giác ABE hay D là trung điểm AE
\(\Rightarrow\) I là trọng tâm tam giác SAE
\(\Rightarrow\dfrac{SI}{SD}=\dfrac{2}{3}\)

a Xem lại đề => Không làm được ý c
a, Gọi :
\(DB\cap AC=\left\{G\right\}\)
\(IE\cap SG=\left\{J\right\}\)
\(AJ\cap SC=\left\{H\right\}\)
\(\rightarrow\left(AIE\right)\cap\left(SBC\right)=HE\)

a. Xem lại đề > không làm được c
b. Gọi \(DB\cap AC=G\)
\(IE\cap SG=J\)
\(AJ\cap SC=H\)
\(\rightarrow\left(AIE\right)=\left(SBC\right)=HE\)
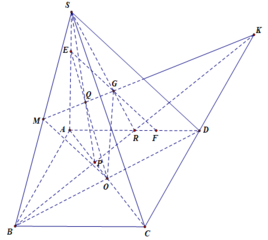

Đây là bài 2 nè bạn :>>
Hình 2 -> hình 3 -> hình 4 -> hình 1