Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\left(\frac{1}{3}-2x\right)^{2018}+\left(3y-x\right)^{2020}\le0\)(1)
Vì \(\left(\frac{1}{3}-2x\right)^{2018}\ge0\forall x\); \(\left(3y-x\right)^{2020}\ge0\forall x,y\)
\(\Rightarrow\left(\frac{1}{3}-2x\right)^{2018}+\left(3y-x\right)^{2020}\ge0\forall x,y\)(2)
Từ (1), (2) \(\Rightarrow\left(\frac{1}{3}-2x\right)^{2018}+\left(3y-x\right)^{2020}=0\)
\(\Leftrightarrow\hept{\begin{cases}\frac{1}{3}-2x=0\\3y-x=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=\frac{1}{6}\\y=\frac{1}{18}\end{cases}}\)
\(\Rightarrow\frac{1}{x}+\frac{1}{y}=6+18=24\left(đpcm\right)\)

(1/3 -2x)^2018 + (3y-x)^2020 <=0
Mà (1/3 -2x) ^ 2018 >= 0 với mọi x ( vì số mũ chẵn)
(3y-x) ^ 2020 >= 0 với mọi x,y ( vì số mũ chẵn)
=> 1/3 - 2x =0 và 3y-x=0
+) 1/3 -2x =0
=> 2x= 1/3 -0 = 1/3
=> x= 1/3 : 2 =1/6
+) 3y-x =0
=> 3y - 1/6 = 0 (vì x = 1/6)
=> 3y = 1/6
=> y = 1/6 : 3 = 1/18
Có 1/x + 1/y = 1 : (1/6) + 1: (1/18) = 6+18 =24 (đpcm)

Bạn nên gõ đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để mọi người hiểu đề của bạn hơn.

Vì \(\left(2x-5\right)^{2020}\ge0\forall x\); \(\left(5y+1\right)^{2022}\ge0\forall y\)
\(\Rightarrow\left(2x-5\right)^{2020}+\left(5y+1\right)^{2022}\ge0\forall x,y\)
mà \(\left(2x-5\right)^{2020}+\left(5y+1\right)^{2022}\le0\)( giả thuyết )
Dấu " = " xảy ra \(\Leftrightarrow\hept{\begin{cases}2x-5=0\\5y+1=0\end{cases}}\Leftrightarrow\hept{\begin{cases}2x=5\\5y=-1\end{cases}}\Leftrightarrow\hept{\begin{cases}x=\frac{5}{2}\\y=\frac{-1}{5}\end{cases}}\)
Vậy \(x=\frac{5}{2}\)và \(y=\frac{-1}{5}\)
( 2x - 5 )2020 + ( 5y + 1 )2022 ≤ 0
Ta có : ( 2x - 5 )2020 ≥ 0 ∀ x
( 5y + 1 )2022 ≥ 0 ∀ y
=> ( 2x - 5 )2 + ( 5y + 1 )2022 ≥ 0 ∀ x, y
Kết hợp với đề bài => Chỉ xảy ra trường hợp ( 2x - 5 )2020 + ( 5y + 1 )2022 = 0
Khi đó \(\hept{\begin{cases}2x-5=0\\5y+1=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=\frac{5}{2}\\y=-\frac{1}{5}\end{cases}}\)

Ta có: \(\left(2x-8\right)^{2000}+\left(3y+4\right)^{2022}\le0\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x-8=0\\3y+4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x=8\\3y=-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=4\\y=-\dfrac{4}{3}\end{matrix}\right.\)

a, (5x+7)(2x-1) <0
<=> \(\hept{\begin{cases}5x+7< 0\\2x-1>0\end{cases}}\)<=> \(\hept{\begin{cases}5x< 7\\2x< 1\end{cases}}\)
<=> \(\hept{\begin{cases}5x+7>0\\2x-1< 0\end{cases}}\)<=> ..................
(5x+7)(2x-1) =0
<=> \(\orbr{\begin{cases}5x+7=0\\2x-1=0\end{cases}}\)<=> ..................

c) Ta có(x-1)2 >= 0 với mọi x
(y+3)2>=0 với mọi c
=> (x-1)2+(y+3)2 >= 0 với mọi x,y
Dấu bằng xảy ra khi và chỉ khi
(x-1)2=0 và (y+3)2=0
=> x=1 và y=-3

Ta có: \(\left(\dfrac{1}{3}-2x\right)^{2018}\ge0\forall x\);
\(\left(3y-x\right)^{2020}\ge0\forall x;y\)
=> \(\left(\dfrac{1}{3}-2x\right)^{2018}+\left(3y-x\right)^{2020}\ge0\)
mà theo đề thì:\(\left(\dfrac{1}{3}-2x\right)^{2018}+\left(3y-x\right)^{2020}\le0\)
=> Dấu ''='' xảy ra khi và chỉ khi: \(\left\{{}\begin{matrix}\dfrac{1}{3}-2x=0\\3y-x=0\end{matrix}\right.\)
Ta có: \(\dfrac{1}{3}-2x=0\Rightarrow x=\dfrac{1}{6}\);
\(3y-x=0\Leftrightarrow3y-\dfrac{1}{6}=0\Leftrightarrow3y=\dfrac{1}{6}\Leftrightarrow y=\dfrac{1}{18}\)
=> \(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{\dfrac{1}{6}}+\dfrac{1}{\dfrac{1}{18}}=6+18=24\left(đpcm\right)\)
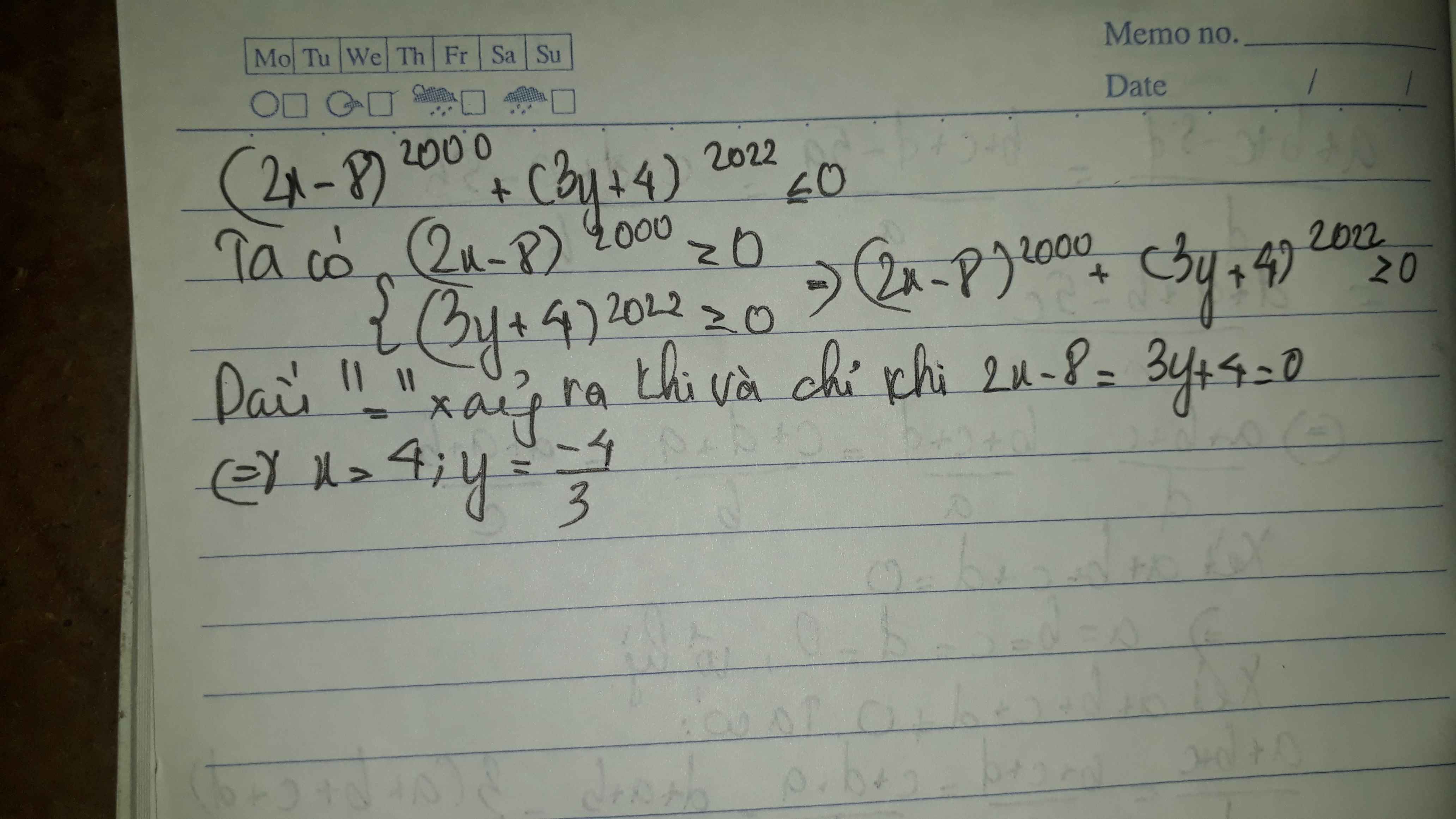
Sửa: \(\left(\dfrac{1}{3}-2x\right)^{2020}+\left(3y-x\right)^{2022}\le0\)
Mà \(\left(\dfrac{1}{3}-2x\right)^{2020}+\left(3y-x\right)^{2022}\ge0\) với mọi x,y
Do đó \(\left\{{}\begin{matrix}\dfrac{1}{3}-2x=0\\3y-x=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{6}\\y=\dfrac{1}{18}\end{matrix}\right.\)
\(\Leftrightarrow\dfrac{1}{x}+\dfrac{1}{y}=6+18=24\)