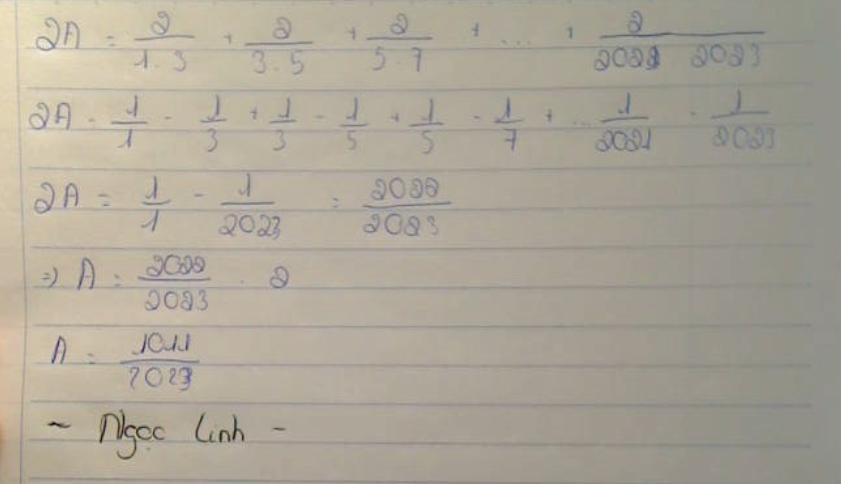K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NH
2
C
6 tháng 5 2022
\(P=\dfrac{1}{1.3}+\dfrac{1}{3.5}+\dfrac{1}{5.7}+...+\dfrac{1}{2021.2023}\)
\(2P=\dfrac{2}{1.3}+\dfrac{2}{3.5}+\dfrac{3}{5.7}+...+\dfrac{2}{2021.2023}\)
\(2P=\dfrac{1}{1}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{2021}-\dfrac{1}{2023}\)
\(2P=\dfrac{1}{1}-\dfrac{1}{2023}\)
\(P=\dfrac{2022}{2023}:2\)
\(P=\dfrac{1011}{2023}\)
TC
6 tháng 5 2022
\(=>P=1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{2021}-\dfrac{1}{2023}\)
\(P=1-\dfrac{1}{2023}=\dfrac{2023}{2023}-\dfrac{1}{2023}=\dfrac{2022}{2023}\)
\(x.P=\dfrac{2022}{2023}=>x=P:\dfrac{2022}{2023}=\dfrac{2022}{2023}:\dfrac{2022}{2023}=1\)
8 tháng 2 2023
Ta có :
\(\dfrac{1}{1.3}\text{=}2\left(\dfrac{1}{1}-\dfrac{1}{3}\right)\)
\(\dfrac{1}{3.5}\text{=}2\left(\dfrac{1}{3}-\dfrac{1}{5}\right)\)
\(\dfrac{1}{5.7}\text{=}2\left(\dfrac{1}{5}-\dfrac{1}{7}\right)\)
\(...\)
\(\dfrac{1}{2021.2023}\text{=}2\left(\dfrac{1}{2021}-\dfrac{1}{2023}\right)\)
\(\Rightarrow\) biểu thức chỉ còn :
\(2.1-\dfrac{2}{2023}\text{=}\dfrac{4044}{2023}\)
8 tháng 2 2023
đặt biểu thức trên là A
ta có
2A=2/1.3+2/3.5+...+2/2021.2023
2A=1/1-1/3+1/3-1/5+...+1/2021-1/2023
2A=1/1-1/2023
2A=2022/2023
A=(2022/2023):2
A=1011/2023
NT
6
J
2
NH
20 tháng 3 2023
\(A=\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+\dfrac{2}{5\cdot7}+...+\dfrac{2}{2021\cdot2023}\)
\(A=\dfrac{1}{1}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{2021}-\dfrac{1}{2023}\)
\(A=\dfrac{1}{1}-\dfrac{1}{2023}\\ A=\dfrac{2023}{2023}-\dfrac{1}{2023}\\ A=\dfrac{2022}{2023}\)
20 tháng 3 2023
A=21.3+23.5+...+297.99�=21.3+23.5+...+297.99
A=11−13+13−15+...+197−199�=11−13+13−15+...+197−199
A=11−199�=11−199
A=9899
=
21−51+51−71+....+951−981
=12−198=21−981tự làm tiếp nha ( giống câu a)
NN
1
11 tháng 5 2016
\(\left(1+\frac{1}{1.3}\right).\left(1+\frac{1}{2.4}\right).\left(\frac{1}{3.5.}\right).....\left(1+\frac{1}{99.101}\right)\)
\(=\frac{4}{3}.\frac{9}{8}.\frac{16}{15}.....\frac{10000}{9999}\)
\(=\frac{2^2}{1.3}.\frac{3^2}{2.4}.\frac{4^2}{3.5}.....\frac{100^2}{99.101}\)
\(=\frac{2^2.3^2.4^2.5^2.....98^2.99^2.100^2}{1.2.3^2.4^2.5^2......99^2.100.101}\)
\(=\frac{2.100}{1.101}\)
\(=\frac{200}{101}\)
TN
1
6 tháng 4 2022
\(C=\left(1+\frac{1}{1.3}\right)\)\(.\left(1+\frac{1}{2.4}\right)\)\(.\left(1+\frac{1}{3.5}\right)\)\(.\left(1+\frac{1}{2014.2016}\right)\)
\(=\frac{2^2}{1.3}.\frac{3^2}{2.4}.\frac{4^2}{3.5}...\frac{2015^2}{2014.2016}\)
\(=\frac{2.2}{1.3}.\frac{3.3}{2.4}.\frac{4.4}{3.5}...\frac{2015.2015}{2014.2016}\)
\(=\frac{\left(2.3.4...2015\right).\left(2.3.4...2015\right)}{\left(1.2.3...2014\right).\left(3.4.5...2016\right)}\)
\(=\frac{2015.2}{2016}\)
\(=...\)(tự tinhs)
DD
0