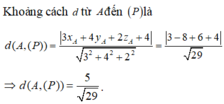Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
$M$ nằm trên $Oy$ nên gọi tọa độ điểm $M$ là \((0,a,0)\)
Vì $M$ cách đều $A,B$ nên \(MA=MB\Leftrightarrow MA^2=MB^2\)
\(\Leftrightarrow (1-0)^2+(a-2)^2+(0+1)^2=(0+2)^2+a^2+(0-5)^2\)
\(\Leftrightarrow a^2-4a+6=a^2+29\)
\(\Leftrightarrow 29+4a=6\rightarrow a=\frac{-23}{4}\)
Vậy tọa độ điểm $M$ là \(\left(0,\frac{-23}{4},0\right)\)

Chọn B
Do G là trọng tâm tam giác ABC => G(2;3;1).
Gọi H là hình chiếu vuông góc của G trên mặt phẳng (Oxz), khi đó GH là khoảng cách từ G đến mặt phẳng (Oxz), ta có:
![]()
Với M là điểm thay đổi trên mặt phẳng (Oxz)
![]()
do đó GM ngắn nhất ⇔ M ≡ H
Vậy độ dài GM ngắn nhất bằng 3