Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1\(\frac{1}{2}\)=3/2
Ta có a/b=3/2
=>a*2=b*3
=>2a=3b(1)
Mà a-b=8
=>a=8+b
Thay a=8+b vào (1) ta có
2*(8+b)=3b
16+2b=3b
16=3b-2b
16=b
=>b=16
=>a=16+8
=>a=24
Giải:
đổi 1\(\frac{1}{2}\)=\(\frac{3}{2}\)
ta có sơ đồ:
số a:!----!----!----!
số b:!----!----!
hiệu số phần bằng nhau là:
3-2=1(phần)
số a là:
8:1*3=24
số b là:
24-8=16
đáp số:số a:24
số b:16

Bài 1:a=b*\(\frac{m}{n}\)
Bài 2:b=a:\(\frac{3}{2}\)
Bài 3:cho hỏi tỉ số % hở

ta có sơ đồ:
STN: |----------|----------|----------|
ST2: |----------|--------|1|
1/3 của số thứ nhất là:
8 - 1 = 7 (đơn vị)
Số thứ nhất là:
7 x 3 = 21
Số thứ 2 là:
21 - 8 = 13
Đáp số: Số thứ nhất: 21
Số thứ hai: 13
Gọi hai số tự nhiên cần tìm là a và b
ta có:2/3a-1=b và a-b=8
Từ 2/3a-1=b=>2/3a=b+1
=>2/3.(b+8)=b+1
=>2/3b+16/3=b+1
=>2/3b-b=1-16/3
=>-1/3b=-13/3=>-b/3=-13/3=>-b=-13=>b=13
khi đó a-b=8=>a=b+8=13+8=21
Vậy.........

Gọi p/s thứ nhất là \(\dfrac{1}{x}\), p/s thứ 2 là \(\dfrac{1}{y}\), p/s thứ 3 là \(\dfrac{1}{z}\)
Theo đề bài ta có : \(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}=1\) (1)
và \(\dfrac{1}{x}-\dfrac{1}{y}=\dfrac{1}{z}\); \(\dfrac{1}{x}+\dfrac{1}{y}=5\cdot\left(\dfrac{1}{z}\right)\).
Thay biểu thức \(\dfrac{1}{x}+\dfrac{1}{y}=5\cdot\left(\dfrac{1}{z}\right)\) trên vào (1) ta được :
\(5\cdot\left(\dfrac{1}{z}\right)+\dfrac{1}{z}=1\Rightarrow z=6\) Vậy phân số thứ ba là \(\dfrac{1}{6}\).
Ta có : \(\left\{{}\begin{matrix}\dfrac{1}{x}-\dfrac{1}{y}=\dfrac{1}{6}\\\dfrac{1}{x}+\dfrac{1}{y}=5\cdot\dfrac{1}{6}\end{matrix}\right.\left(Đề-bài\right)\)
Bài toán tổng hiệu \(\dfrac{1}{x}\) là số lớn, \(\dfrac{1}{y}\) là số bé (do \(\dfrac{1}{x}-\dfrac{1}{y}\) ra số dương).
Vậy \(\dfrac{1}{x}=\dfrac{\left(\dfrac{1}{6}+5\cdot\dfrac{1}{6}\right)}{2}=\dfrac{1}{2}\); \(\dfrac{1}{y}=5\cdot\dfrac{1}{6}-\dfrac{1}{2}=\dfrac{1}{3}\)
Vậy phân số thứ nhất là \(\dfrac{1}{2}\), phân số thứ hai là \(\dfrac{1}{3}\), phân số thứ ba là \(\dfrac{1}{6}\).

gọi số cây của đội \(1;2;3\) đã trồng lần lược là \(a;b;c\) \(\left(0< a;b;c\in Z\right)\)
vì \(\dfrac{1}{2}\) số cây của đội \(1\) trồng bằng \(\dfrac{2}{3}\) số cây của đội \(2\) và bằng \(\dfrac{3}{4}\) số cây của đội \(3\)
\(\Rightarrow\dfrac{1}{2}a=\dfrac{2}{3}b=\dfrac{3}{4}c\) (1)
vì số cây của đội \(2\) trồng ít hơn tổng số cây của đội \(1\) và \(3\) là \(55\) cây
\(\Rightarrow b+55=a+c\) (2)
từ (1) và (2) ta có : \(\left\{{}\begin{matrix}a=60\\b=45\\c=40\end{matrix}\right.\left(tm\right)\)
vậy ..............................................................................................................................
Gọi a,b,c lần lượt là số cây của 3 đội 1,2,3 Theo đề ta có: 1/2a=2/3b=3/4c (1) và a+c-b=55 Ta lấy (1) chia cho BCNN(1,2,3)=6, ta được như sau: a/12=b/9=c/8 và a+c-b=55 Áp dụng t/c tỉ số bằng nhau, ta có a/12=b/9=c/8=a+c-b/12+8-9=55/11=5 Suy ra a=12.5=60; b=9.5=45; c=8.5=40

Gọi các phân số cần tìm là x, y, z.
Tổng của ba phân số bằng 1 nên:
x + y + z = 1 (1)
Hiệu của phân số thứ nhất và thứ hai bằng phân số thứ ba nên:
x - y = z (2)
Tổng của phân số thứ nhất và thứ hai bằng 5 lần phân số thứ ba nên:
x + y = 5z (3)
Từ (1), (2), (3) ta có hệ:
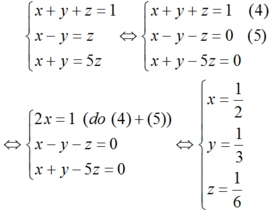
Vậy ba phân số cần tìm lần lượt là:
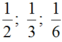

Gọi số cần tìm là ab
Mà số đó gấp 7 lần tổng các chữ số của nó
\(\Rightarrow\)ab=7.(a+b)
Ta có:ab=7.(a+b)
10a+b=7a+7b
10a-7a=7b-b
3a=6b(1)
Từ 1 suy ra được a=6;b=3
Vậy số cần tìm là 63
Câu2:
Gọi số cần tìm là ab
Mà số đó gấp 8 lần tổng các chữ số của nó
\(\Rightarrow\)ab=8x(a+b)
Ta có:ab=8x(a+b)
10a+b=8a+8b
10a-8a=8b-b
2a=7b(1)
Từ(1) suy ra a=7;b=2
Vậy số cần tìm là 72

Một hàm số cho bởi công thức y = f(x) mà không chú thích gì về tập các định thì ta quy ước rằng tập xác định của hàm số ấy là tập hợp tất cả x ∈ R sao cho biểu thức f(x) có nghĩa.
Hàm số \(y=\dfrac{x+1}{\left(x+1\right)\left(x^2+2\right)}\) có tập xác định là D = R/{-1}, còn hàm số \(y=\dfrac{1}{x^2+2}\). Do đó hai hàm số khác nhau (mặc dù rằng với mọi x ≠ -1 giá trị của hàm số luôn bằng nhau khi x lấy cùng một giá trị.
Gọi a, b là hai số cần tìm. Ta có hệ phương trình:
\(\left\{ {\begin{array}{*{20}{c}} {a + b = 54}\\ {\frac{a}{b} = \frac{1}{2}} \end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {b = 2a}\\ {a+2a=3a = 54} \end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {a = 18}\\ {b = 2a = 2.18 = 36} \end{array}} \right.\)